神经网络基础

Posted 2023-03-15 Keep--Silent

第08天:初始深度学习

• • 第08天：初始深度学习-神经网络基础(1)
  • • 5-深度学习要解决的问题 ：
    • 6-深度学习应用领域
    • 7-计算机视觉任务
    • 8-视觉任务中遇到的问题
    • 9-得分函数
    • 10-损失函数的作用
    • 11-前向传播整体流程
  • 第08天：初始深度学习-神经网络基础(2)
  • • 1-反向传播计算方法
    • 2-神经网络整体架构
    • 3-神经网络架构细节
    • 4-神经元个数对结果的影响
    • 5-正则化与激活函数
    • 6-神经网络过拟合解决方法

第08天：初始深度学习-神经网络基础(1)

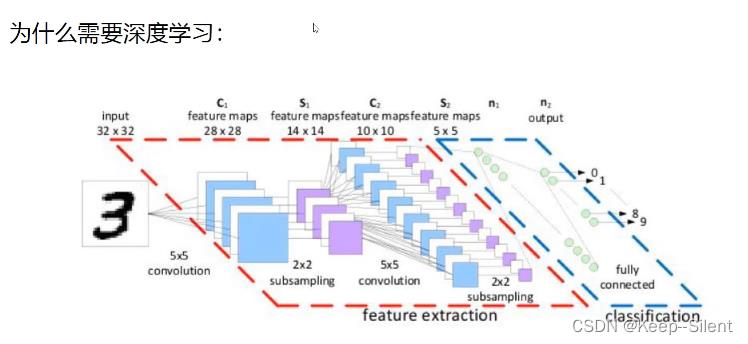
5-深度学习要解决的问题 ：

深度学习要解决的问题 ：提取特征
机器学习流程：

1. 数据获取
2. 特征工程
3. 建立模型
4. 评估与应用

特征工程的作用：

1. 数据特征决定了模型的上限
2. 预处理和特征提取是最核心的
3. 算法和参数选择决定了如何逼近这个上限

特征提取

1. 传统提取：找特征难
   
2. 深度学习：
   

6-深度学习应用领域

7-计算机视觉任务

8-视觉任务中遇到的问题

机器学习常规套路：

1. 收集数据并给定标签
2. 训练一个分类器
3. 测试，评估

K近邻算法：

1. 计算一直类别数据集中的点与当前点的距离
2. 按距离以此排序
3. 选取与当前距离最小的k个点
4. 确定前k个点所在类别的出现概率
5. 返回前k个点出现频率最高的类别作为当前点预测分类

使用k近邻会使得背景相同的分为同类，并不适合

9-得分函数

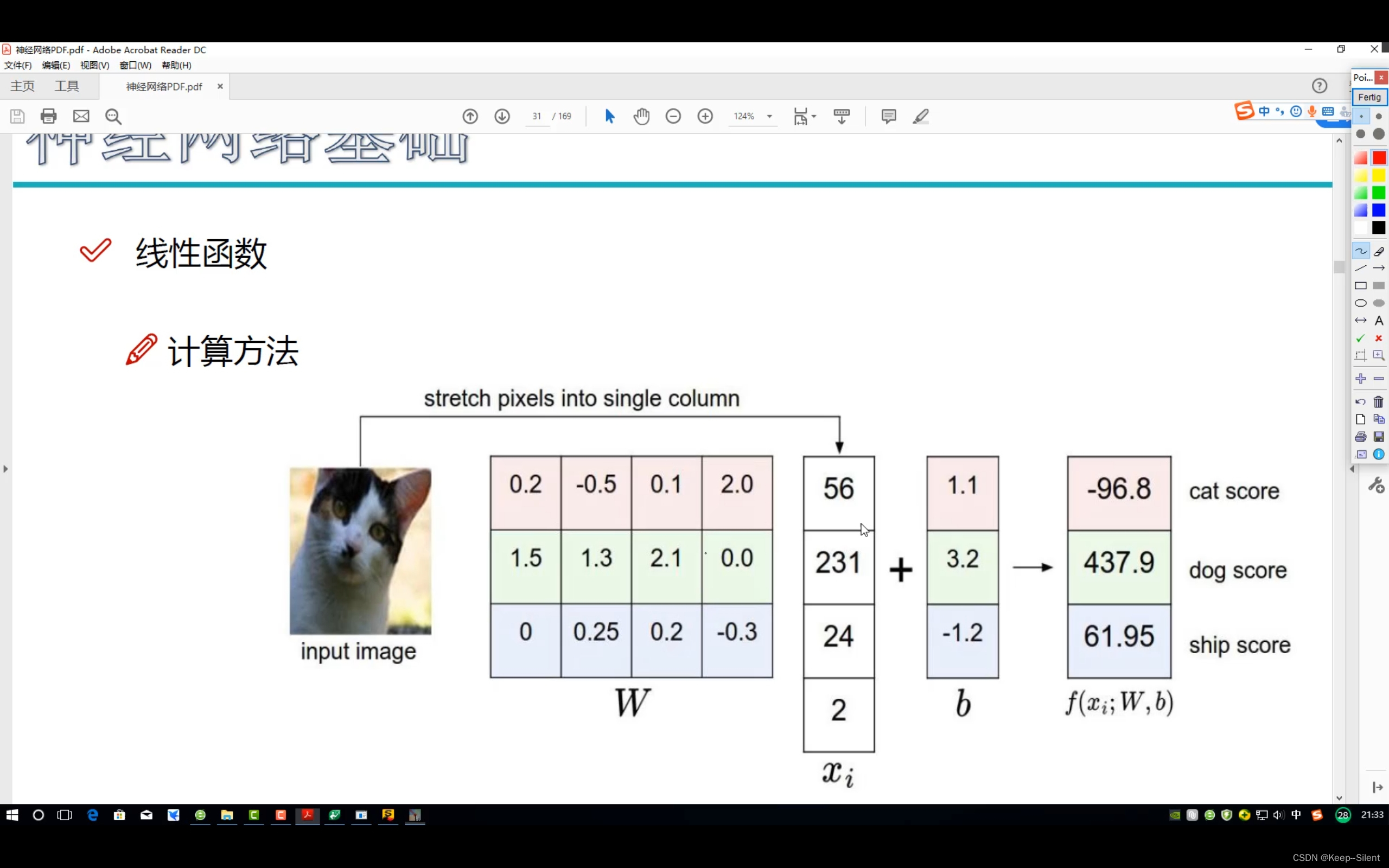
1. 线性函数：
   从输入到输出的映射
   x:img(32*32*3=3072),W:权重参数,b(偏执参数)
   f(x,W)=Wx
   W:1*3072;x:3072*1

假设3类，图片img(2*2*1)
W=3*4;x=4*1;b=3*1
f=WX+b。

2. 损失函数
   如$L_i={\sum }_{j\ne y_i}\max (0,s_j-s_{y_i}+1)$
   

10-损失函数的作用

损失函数=数据损失+正则化惩罚项
$L=\frac{1}{N}{\sum }_{i=1}^N{\sum }_{j\ne y_i}\max (0,f(x_i;W{)}_j-f(x_i;W{)}_{y_i}+1)+\boxed{\lambda R(W)}$
$R(W)={\sum }_k{\sum }_l{W}_{k,l}^2$
防止过拟合

Softmax分类器
归一化：$P(Y=k|X=x_i)=\frac{e^{{\ast }_k}}{{\sum }_i{e}^{{\ast }_j}}\text{where}s=f(x_i;W)$
计算损失值：$L_i=-\log P(Y=y_i|X=x_i)$

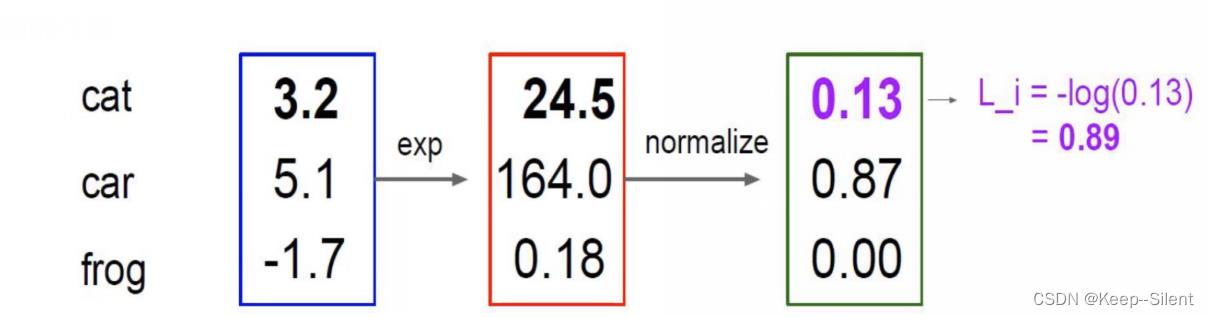
11-前向传播整体流程

第08天：初始深度学习-神经网络基础(2)

1-反向传播计算方法

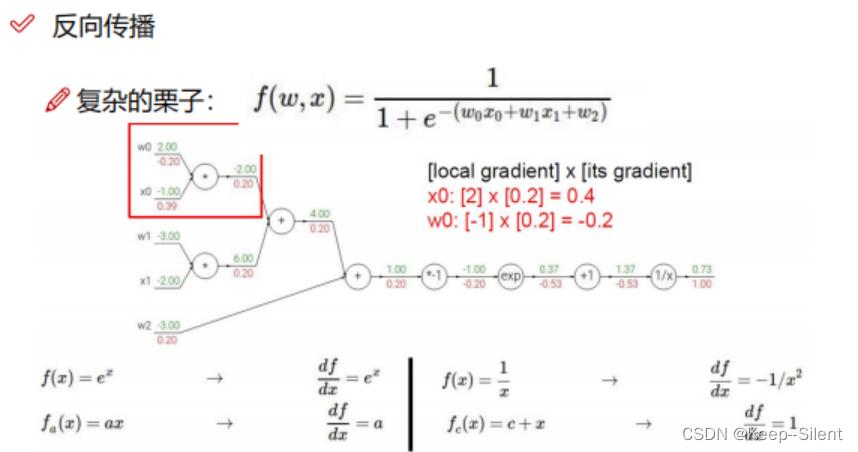
加法门单元：均等分配
MAX门单元：给最大的
乘法门单元：互换的感觉

2-神经网络整体架构

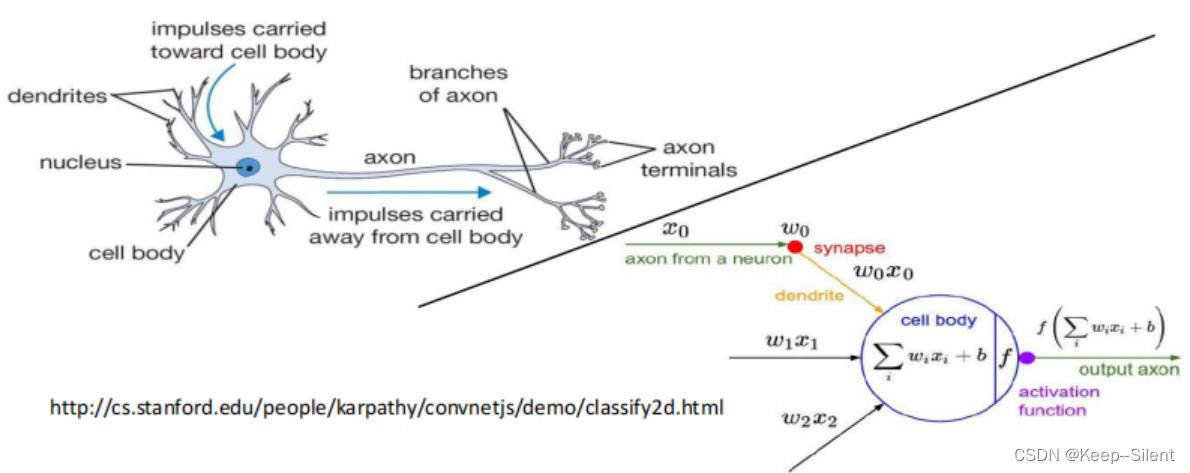
整体架构

1. 层次结构
2. 神经元
3. 全连接
4. 非线性
   

3-神经网络架构细节

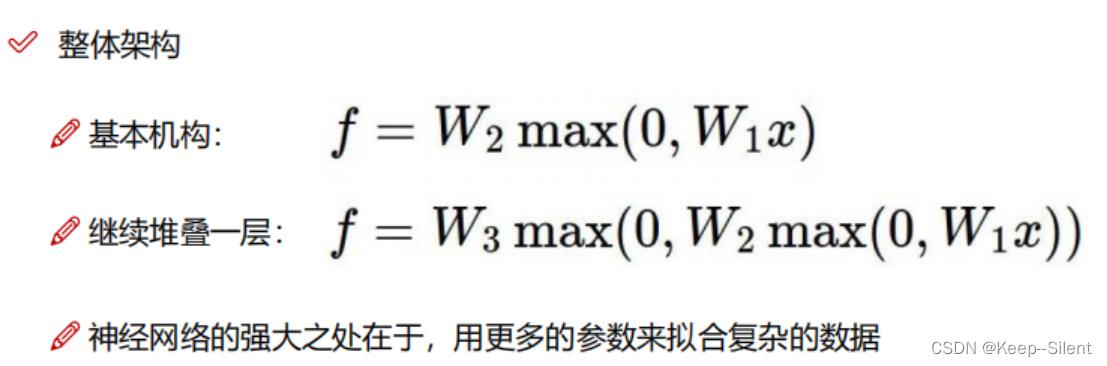
4-神经元个数对结果的影响

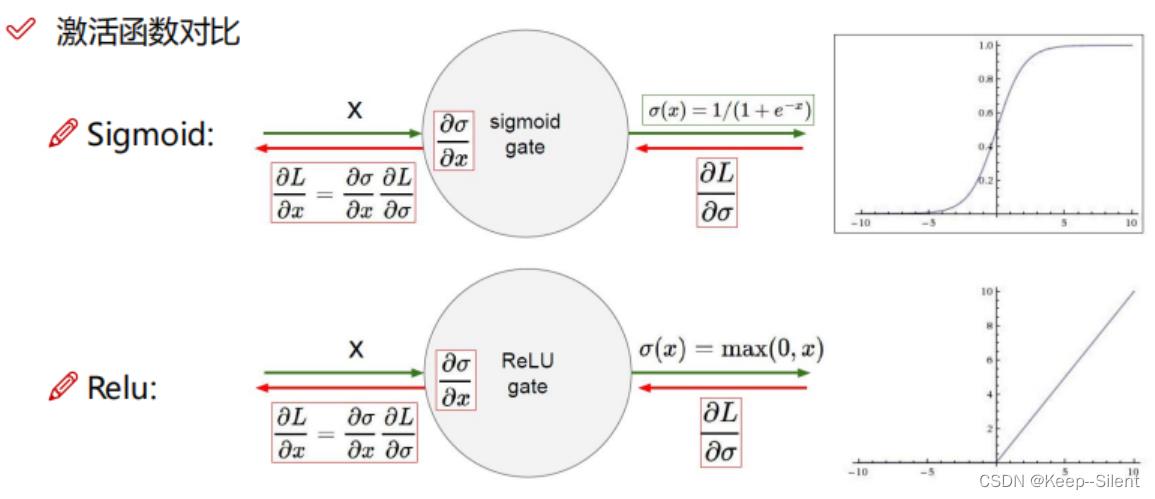
5-正则化与激活函数

Sigmoid和Relu
Sigmoid：当数值过大或者过小，梯度消失。
Relu：当前使用得较多

1. 数据预处理：
   1. 中心化
   2. 正则化
      
2. 参数初始化
   1. 通常我们都使用随机策略来进行参数初始化
      $\mathrm{W}=0.01\ast np.random.randn(\mathrm{D},\mathrm{H})$

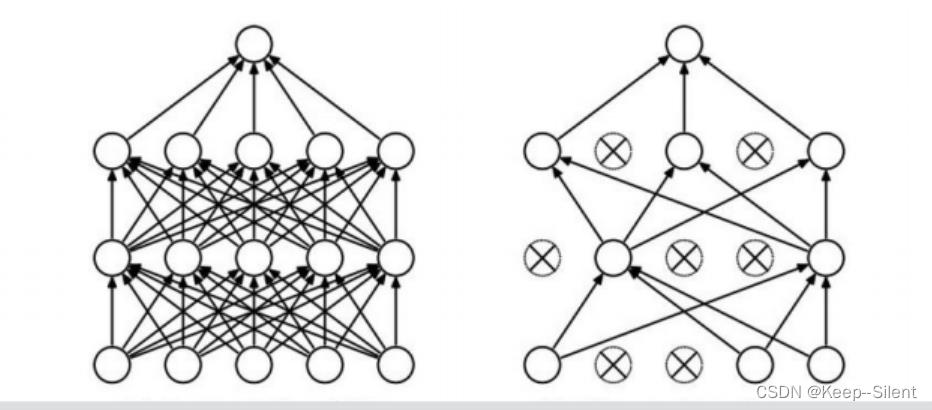
6-神经网络过拟合解决方法

过拟合是神经网络非常头疼的一个大问题：DROP-OUT随机杀死一些神经元