Trimmed 稳健均值估计与 中位数-中位数配对偏差法估计标准差——理论与 Python 实现

Posted 2023-03-09 zhuo木鸟

文章目录

• a-Trimmed 平均
• • 理论步骤
  • Python 实现
• 中位数-中位数绝对偏差
• • 理论步骤
  • Python 实现

本文主要根据标准 16269-4:2010 的条款 5.2.2 和 5.3.1 。

数据集为：$x_1,x_2,\cdots ,x_n$， $n$ 是样本容量。

a-Trimmed 平均

a-Trimmed 的平均值的计算，是通过截断次序统计量的“头尾”，从而进行稳健估计，截取比例为 $\alpha$。

理论步骤

给定一个系数 $\alpha \in [0,0.5)$，即样本的次序统计量为： $x_{(1)},x_{(2)},\cdots ,x_{(n)}$。

计算出截取比例 $\alpha$ 对应的截取个数 $r=[\alpha \cdot n]$，其中 $[\alpha \cdot n]$ 为计算小于 $\alpha \cdot n$ 的最大整数。并计算 $\alpha \cdot n$ 的浮点数部分为：$g=\alpha \cdot n-r$。

从而计算出 a-trimmed 均值为：
$$\bar{x}(\alpha )=\frac{1}{n(1-2\alpha )}[(1-g)(x_{(r+1)}+x_{(n-r)})+\sum _{i=r+2}^{n-r-1}{x}_{(i)}]$$

即抛弃头尾 r 个数据（升序排序后），在将删除 r 个后，两个极端数据，按权重 $(1-g)$ 计算其影响。

Python 实现

def trimmed_mean(x, alpha=0.05):
    if isinstance(x, pd.Series) or isinstance(x, pd.DataFrame):
        x = x.astype('float').values
    if isinstance(x, list):
        x = np.array(x)
    # 样本个数
    n = len(x)
    r = int(alpha*n)
    g = alpha*n - r
    
    x_sorted = np.sort(x)
    coeff = 1/(n*(1-2*alpha))
    
    loc = coeff*((1-g)*(x_sorted[r] + x_sorted[n-r-1]) + sum(x_sorted[r+1:n-r-1]))
    return loc

中位数-中位数绝对偏差

理论步骤

$$S_n=s_n\times {\text{Median}}_i({\text{Median}}_j|x_j-x_i|,i\ne j,j=1,2,\cdots ,n)$$
该式为对 $1,2,\cdots ,n$ 每个 $x_i$，计算 $\text{Median}|x_j-x_i|，j\ne i,j$ 为除了 $x_i$ 之外的其他样本，从而得到 n 个中位数样本，之后，再在这些中位数样本中，选取出中位数，配合 $s_n$ 进行计算。

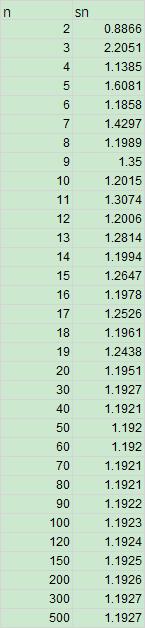
$s_n$ 为 ISO 16269-4:2010 的附件表 D.1 中规定的系数（具体怎么求，我也不清楚，有大神可补充的，在此感谢），表格如下：

Python 实现

将上述表格放在一个叫 correction_factor.xlsx 的 Excel 表格中，与代码文件在同一路径下：

def median_median_absolute_pairwise(x):
    if isinstance(x, pd.Series) or isinstance(x, pd.DataFrame):
        x = x.astype('float').values
    if isinstance(x, list):
        x = np.array(x)
    # 样本个数
    n = len(x)
    path = r'./correction_factors.xlsx'
    factor_data = pd.read_excel(path, header=0)
    n_list = factor_data['n']
    if n not in n_list:
        if n <= 150:
            n_list_interpolate = np.arange(2, 151)
            sn_list = factor_data['sn'].values
            f = interpolate.interp1d(n_list, sn_list, kind='cubic')
            sn_list = f(n_list_interpolate)
            sn = sn_list[n-2]
        elif 150 < n and n <= 200:
            sn = 0.9914
        elif 200 < n and n<=300:
            sn = 0.9912
        else:
            sn = 0.9910
    else:
        sn = factor_data.loc[factor_data['n']==n]['sn']
    
    sn = float(sn)
    pairwise_mad = []
    for i in range(n):
        x_exclude = np.delete(x, np.where(x==x[i]))
        diff = np.abs(x_exclude - x[i])
        diff_med = np.median(diff)
        pairwise_mad.append(diff_med)
    
    pairwise_mad = np.array(pairwise_mad)
    pairwise_mad_med = np.median(pairwise_mad)
    scale = sn*pairwise_mad_med
            
    return scale