Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记

Posted 2023-03-09 mutourend

1. 引言

前序博客有：

• Lurk——Recursive zk-SNARKs编程语言
• rank-1 constraint system R1CS
• Spartan中 Vitalik R1CS例子 SNARK证明基本思路

微软团队2021年论文 《Nova: Recursive Zero-Knowledge Arguments from Folding Schemes》。
开源代码见：

• https://github.com/Microsoft/Nova（Rust）

---

作者视频讲解见：

• 2022年2月 Nova: Recursive Zero-Knowledge Arguments from Folding Schemes - Srinath Setty

Nova为：

• a SNARK for iterative computations：用于证明$y=F(F(F(F(F(x)))))$，其中：
  • $F$为（potentially non-deterministic）computation
  • $x$为输入，$y$为输出

Nova这样的iterative computation SNARK的应用场景有：

• VDFs：此时$F$为某delay function，如MinRoot，计算某有限域内的cube root 或 fifth root。
• Rollups：$F$的输入为：state Merkle root，以及，某些交易（non-deterministically），执行交易，输出：updated Merkle root。
• Turing-complete SNARK语言（如Lurk）的后端：$F$为执行a “step” of the program。

Nova的关键特性为：

• 无需trusted setup
• 无需（如，通过FFT运算）做多项式除法和多项式乘法运算
  • 可基于任意cycles of curves，如secp/secq。【详情见Spartan-ECDSA：最快的浏览器内 ZK secp256k1 ECDSA中的“附录：Secp256k1/Secq256k1曲线cycle”。】
  • 也可基于任意FFT-friendly cycles of curves，如Pasta（Pallas/Vesta）。【详情见：Halo2学习笔记——背景资料之Elliptic curves（5） 和 Mina中的Pasta（Pallas和Vesta）曲线。】
• $F$运算指定为R1CS表示
• 为理论上最简单的证明系统，同时提供了state-of-the-art efficiency：
  • Prover time：由2个size为$O(C)$的multiexps主导，其中，$C=|F|$
    • Nova的证明速度要比Groth16/PLONK/Halo等快5~50倍。
  • 具有Constant-sized verifier circuit（主要由2个scalar multiplication运算主导）：意味着具有lowest recursion threshold。
  • 压缩proof size为：$O(\log C)$个group elements：实际上只有数KB。

为证明$y=F^{(n)}(x)$：

• 1）直观方法为：

  • 将$F$的$n$个迭代展开为一个电路

  • 对该单一电路应用某state-of-the-art SNARK来生成证明

    直观方法的缺陷为：

    • Prover所需内存为：$\Omega (n\ast |F|)$
    • proof 不是 incrementally updatable
    • 取决于具体的SNARK方案，Verifier time可能会依赖具体的$n$值（即，迭代次数）
• 2）Incrementally verifiable computation（IVC）[Val08, BCTV14]
  

[Val08, BCTV14] IVC方案 与 Nova对比为：

Nova 与 Bunz等人2021年论文BCLMS21 Proof-Carrying Data without Succinct Arguments中的“split accumulation”相关：

• Nova效率更高、更直接，且提供了a “native” scheme for proof compression。

Nova的秘密武器在于：Folding Schemes for NP：【下图的NP instance均为R1CS instance】

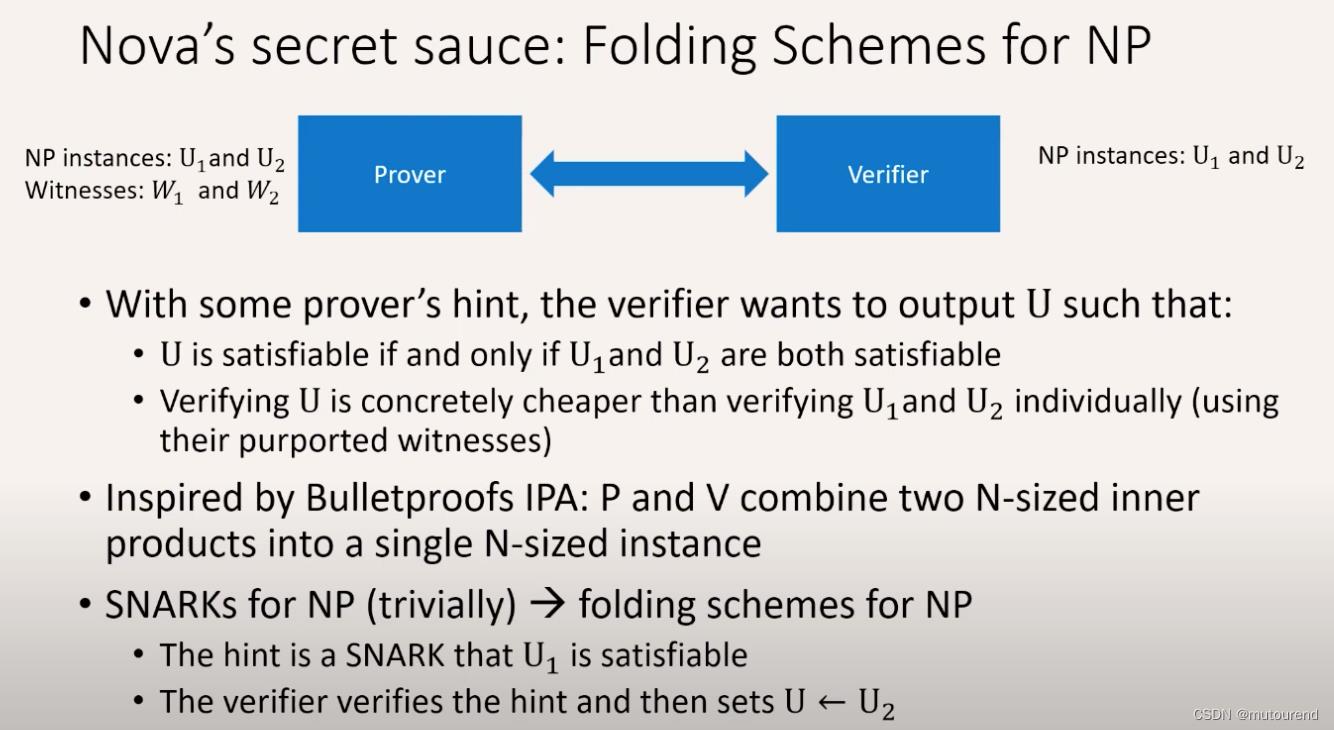
Nova的关键贡献在于：

• 不使用SNARKs 所实现的folding scheme for NP

R1CS回顾：

为实现R1CS的folding scheme，最直观但却错误的方式为：

即以上方案，对于$Z=(W,x,1)$，找不到相应的$r$，使得$AZ\circ BZ\ne CZ$，原因在于：

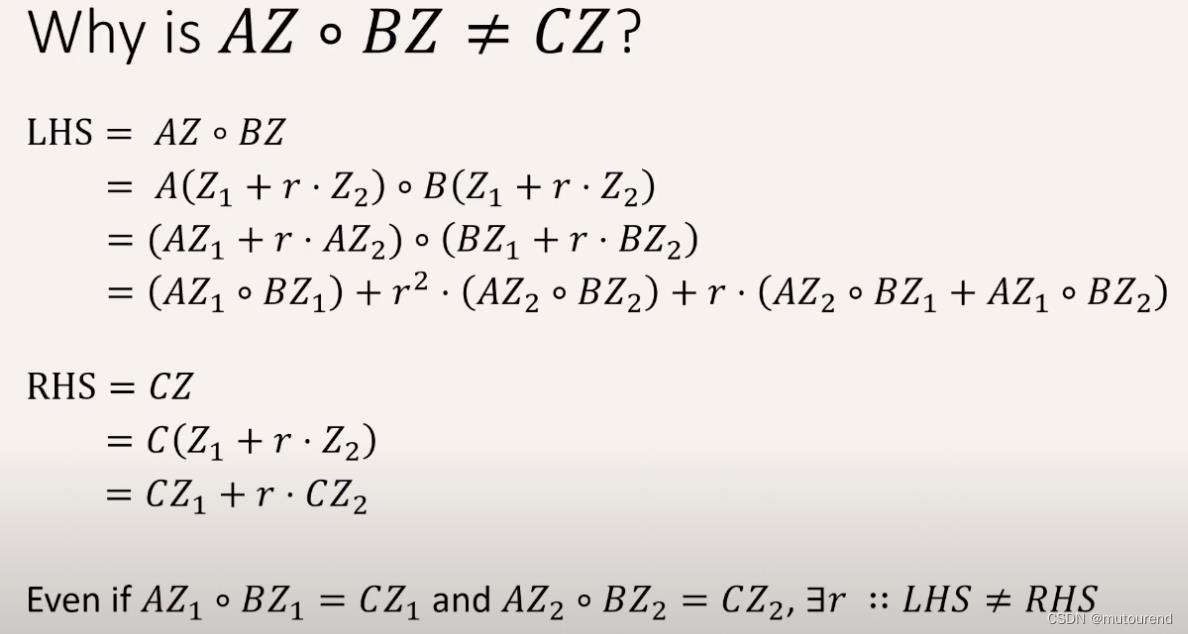
Nova的创新之一在于其所实现的Relaxed R1CS：【当$u=1,E=\vec{0}$时，标准R1CS实例 为 Relaxed R1CS实例 的特例情况。】

针对Relaxed R1CS的folding scheme为：【即通过引入public input $u$和witness $E$来实现消减，以保证folding后仍能满足相同的relation关系】

根据relaxed R1CS的folding scheme所实现的IVC直观方案为：

不过，以上naive方案，IVC proof size为：$O(|F^{\prime }|)$个group elements。且存在以下2个问题：

• Proofs are large, both asymptotically and concretely
• Proofs are not zero-knowledge

原则上：借助zkSNARKs，$P$可证明the knowledge of a valid IVC proof，从而提供了succinctness和zero-knowledge。但是，借助zkSNARKs的方案是expensive的：

• $P$必须证明，如，其知道$W$对应承诺值$\hat{W}$，以及其他信息

为此，Nova创新之二是进行了proof压缩：

• 将对vectors的承诺值，解析为，对multilinear多项式的多项式承诺值
• 使用Spartan的变种，来直接证明承诺值$\hat{W}$满足相应的relaxed R1CS。
• 压缩后的proof size，由$O(|F^{\prime }|)$个group elements，降低为$O(\log |F^{\prime }|)$个group elements

也可以使用IPA（Inner Product Argument）来证明承诺值$\hat{W}$满足相应的relaxed R1CS:

• proof size可降低约5倍（可避免Spartan中的sum-check protocol，但在生成final proof时，会引入稍微高一点的开销）

Navo的缺陷有：

• zero-knowledge被限制在单个prover的context（zero-knowledge属性不是必须的）

当前的情况为：

• IVC proof size为：$O(|F^{\prime }|)$个group elements。
• 压缩的proof size为：$O(\log |F^{\prime }|)$个group elements，但是其不可incremental。

因此，一个open question为：

• 保持Nova其它特性的同时，能否构建具有succinct proof的IVC方案？
  Nova的一些优秀特性有：
  • smallest verifier circuit
  • efficient prover等等

当前的一些进展以及规划为：

---

Nova：

• 为一种新的Incrementally Verifiable Computation（IVC）方案。
• 可递归证明形如$y=F^l(x)$的incremental computation执行的正确性，其中$F$为（potentially non-deterministic）computation，$x$为输入，$y$为输出，且$l>0$。

不同于之前的IVC方案，Nova完全避免了(SN)ARK，引入了一种新的更简单、更弱、更能高效实现的原语——folding scheme：

• 可将 “检查2个instance之间某种关系的任务” reduce为 “检查单个instance”。

参考资料