判断点是不是在多边形内部的方法

Posted 2023-03-09

参考技术A

判断点是否在多边形内部的方法如下：

（1）面积和判别法：判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形，相等则在多边形内部。

（2）夹角和判别法：判断目标点与所有边的夹角和是否为360度，为360度则在多边形内部。

（3）光线投射法：从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。

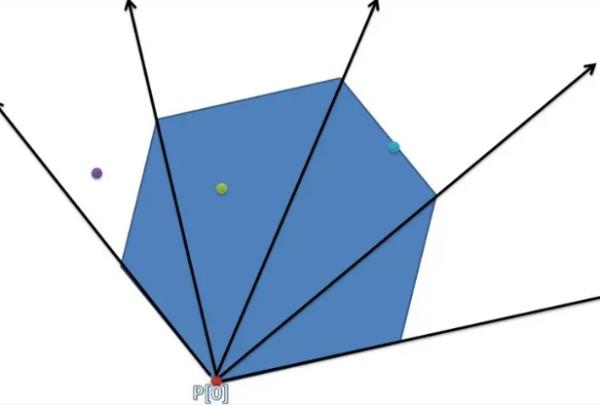
判断一个点是否在一个多边形内

假设多边形的坐标存放在一个数组里，首先我们需要取得该数组在横坐标和纵坐标的最大值和最小值，根据这四个点算出一个四边型，首先判断目标坐标点是否在这个四边型之内，如果在这个四边型之外，那可以跳过后面较为复杂的计算，直接返回false。

if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY)
// 这个测试都过不了。。。直接返回false；

接下来是核心算法部分：

int pnpoly (int nvert, float *vertx, float *verty, float testx, float testy) int i, j, c = 0; for (i = 0, j = nvert-1; i < nvert; j = i++) if ( ( (verty[i]>testy) != (verty[j]>testy) ) &&
(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )c = !c; return c;

首先，参数nvert 代表多边形有几个点。浮点数testx, testy代表待测试点的横坐标和纵坐标，*vertx,*verty分别指向储存多边形横纵坐标数组的首地址。

我们注意到，每次计算都涉及到相邻的两个点和待测试点，然后考虑两个问题：

被测试点的纵坐标testy是否在本次循环所测试的两个相邻点纵坐标范围之内？即verty[i]<testy < verty[j]

或者verty[j] <testy < verty[i]

2. 待测点test是否在i,j两点之间的连线之下？看不懂后半短if statement的朋友请自行在纸上写下i,j两点间的斜率公式，要用到一点初中解析几何和不等式的知识范畴，对广大码农来说小菜一碟。