数据结构与算法图最短路径算法 ( Floyed 算法 | 图最短路径算法使用场景 | 求解图中任意两个点之间的最短路径 | 邻接矩阵存储图数据 | 弗洛伊德算法总结 )

Posted 2023-03-08 韩曙亮

文章目录

• 一、最短路径
• 二、图最短路径算法使用场景
• 三、求解图中任意两个点之间的最短路径
• 四、邻接矩阵存储图数据
• 五、只允许经过 1 号点中转得到任意两点之间的最短路径
• 六、在之前的基础上-只允许经过 1、2 号点中转得到任意两点之间的最短路径
• 七、在之前的基础上-只允许经过 1、2 、...、n 号点中转得到任意两点之间的最短路径
• 八、弗洛伊德算法总结

图的最短路径算法 : 有如下四种 ;

• 弗洛伊德算法 Floyed ;
• 迪杰斯特算法 Dijstra ;
• 贝尔曼-弗洛伊德算法 Bellman-Floyed ;
• SPFA 算法 Shortest Path Faster Algorithm ;

本篇博客介绍 弗洛伊德 算法 ;

一、最短路径

---

在 图 中 , 结点 之间的 边 带有权值 , 则该图就是 带权图 ;

边的 权值 可以理解为 两个结点 之间的 距离 或者 消耗时间 ,

从 结点 A 到 结点 B 有不同的路径 ,

将这些路径的 边 的 权值 相加 , 权值总和最小的路径 , 就是 最短路径 ;

举例说明 : 下图 中 , 求 C4 结点 到 C6 结点 的最短路径 ;

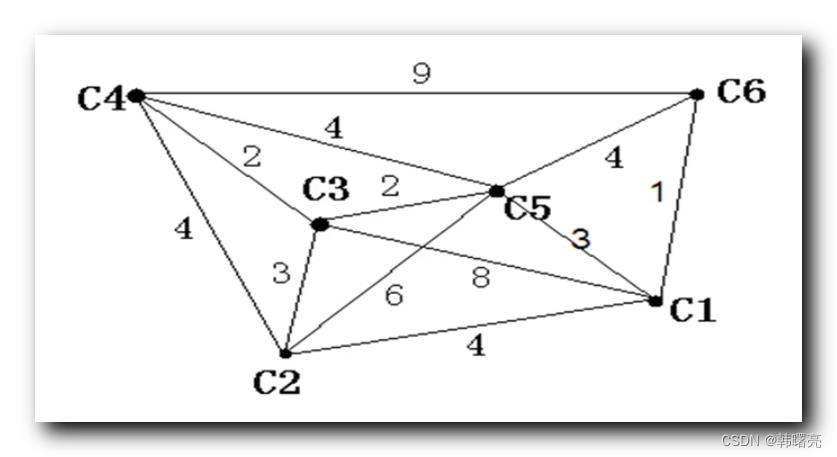
C4 结点 到 C6 结点的路径 :

• C4 -> C6 : 权值累加总和为 9 ;
• C4 -> C5 -> C6 : 权值累加总和为 8 ;
• C4 -> C3 -> C5 -> C6 : 权值累加总和为 8 ;

其它的路径更远 , 可以看到其最短路径是 后两种 , 最短路径为 8 ;

二、图最短路径算法使用场景

---

图最短路径算法使用场景 :

• 管道铺设
• 线路安装
• 地图规划

三、求解图中任意两个点之间的最短路径

---

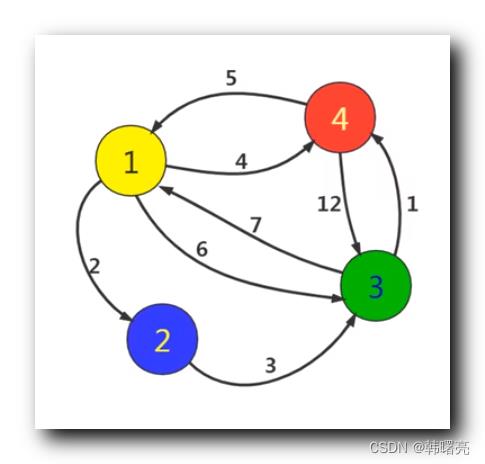
假设图中有任意两个点 , A 点 和 B 点 ,

要令 A 到 B 之间的 距离 变短 , 只能 引入 第三个点 K , A 先到 K , 然后从 K 到 B ,

此时 A -> B 的路径 可能 小于 A -> K -> B 的路程 ;

中转点 的 个数 可能需要多个 , A 到 B 可能中间途径多个 中转点 , 使得 两个结点 之间的距离更短 ;

以上图为例 , 从 结点 4 到 结点 3 的直接距离为 12 ,

如果 找一个途经点 , 从 结点 4 先到 结点 1 , 然后从 结点 1 到 结点 3 , 最终的距离为 11 ;

如果 找 2 个途径点 , 节点 4 -> 结点 1 -> 结点 2 -> 结点 3 , 距离为 10 ;

每个顶点 都有可能 缩短 另外两个 顶点 之间的距离 ;

四、邻接矩阵存储图数据

---

使用 邻接矩阵 存储 下图信息 ;

下图中 使用 二维数组 int[][] edge 存储邻接矩阵 , 二维数组 元素的值为 两个点 之间的 边 的 权重 ;

如 : edge[1][2] 是 从 结点 1 到 结点 2 之间的 边 的权重 ;

邻接矩阵 取值 :

• 两个结点之间存在边 : 邻接矩阵 取值 就是这个 边 的权重 ;
• 两个结点之间不存在边 : 如果 没有可达 的边 , 如 结点 2 -> 结点 1 没有直达的边 , 则距离设置为 无穷大 ;
• 结点到其本身的距离 : 约定为 0 ;

五、只允许经过 1 号点中转得到任意两点之间的最短路径

---

在上述 邻接矩阵 int[][] edge 中 , 求 结点 i 到 结点 j 之间的 最短路径 , 并且只允许从 结点 1 进行中转 ;

结点 i 到 结点 j 的距离为 edge[i][j] ,

结点 i 到 结点 1 的距离为 edge[i][1] , 结点 1 到 结点 j 的距离为 edge[1][j] , 其 总的距离为 edge[i][1] + edge[1][j] ,

如果 edge[i][1] + edge[1][j] < edge[i][j] , 则 结点 i 到 结点 j 之间的距离缩短了 , edge[i][1] + edge[1][j] 就是其当前的 最短路径 ;

// 只允许经过 1 号点中转得到任意两点之间的最短路径
for(int i = 1; i <= n; i++) 
	for(int j = 1; j <= n; j++) 
		if(edge[i][j] > edge[i][1] + edge[1][j]) 
			edge[i][j] = edge[i][1] + edge[1][j];
		
	

更新后的 邻接矩阵 变为下图所示 :

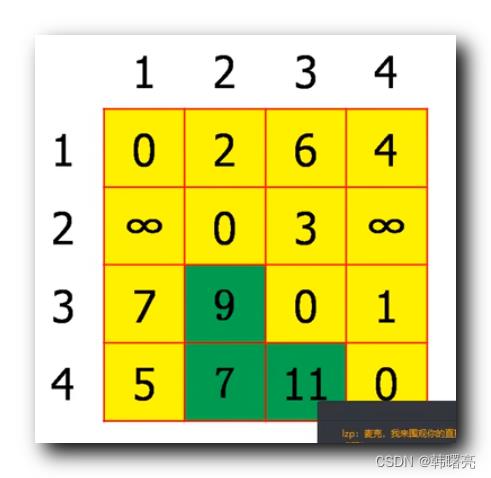
原来 结点 3 -> 结点 2 的 之间没有边 , 距离为 无穷大 , 现在通过 1 中转 , 3 -> 1 -> 2 的距离为 9 , 距离缩短了 ;

原来 结点 4 -> 结点 2 的 之间没有边 , 距离为 无穷大 , 现在通过 1 中转 , 4 -> 1 -> 2 的距离为 7 , 距离缩短了 ;

原来 结点 4 -> 结点 3 的 之间没有边 , 距离为 12 , 现在通过 1 中转 , 4 -> 1 -> 3 的距离为 11 , 距离缩短了 ;

六、在之前的基础上-只允许经过 1、2 号点中转得到任意两点之间的最短路径

---

上一个章节中 , 已经求出 只允许经过 1 号顶点时 , 任意两点的 最短路径 ;

本章节中 , 在上一章节的基础上 , 再求 经过 2 号顶点 , 是否能 得到 任意两个 结点 , 结点 i 到 结点 j 之间的 最短路径 ;

算法代码如下 :

// 只允许经过 1 号点中转得到任意两点之间的最短路径
for(int i = 1; i <= n; i++) 
	for(int j = 1; j <= n; j++) 
		if(edge[i][j] > edge[i][1] + edge[1][j]) 
			edge[i][j] = edge[i][1] + edge[1][j];
		
	


// 只允许经过 1、2 号点中转得到任意两点之间的最短路径
for(int i = 1; i <= n; i++) 
	for(int j = 1; j <= n; j++) 
		if(edge[i][j] > edge[i][1] + edge[1][j]) 
			edge[i][j] = edge[i][1] + edge[1][j];
		
	

原来 结点 1 -> 结点 3 的 距离为 6 , 现在通过 2 中转 , 1 -> 2 -> 3 的距离为 5 , 距离缩短了 ;

原来 结点 4 -> 结点 3 的 距离为 11 , 路径为 4 -> 1 -> 3 , 现在再通过 2 中转 , 4 -> 1 -> 2 -> 3 , 新的距离为 10 , 距离缩短了 ;

七、在之前的基础上-只允许经过 1、2 、…、n 号点中转得到任意两点之间的最短路径

---

经过所有点的遍历 , 也就是经过 1、2 、3、4 号点之后 , 得到的 邻接矩阵 中 , 所有的 任意 两个点之间的距离都是最小距离 ;

代码参考 :

// k 代表结点个数 , 经过 1 ~ n 结点中转 , 每次增加一个点
// 就将 邻接矩阵 中的 最短路径 重新计算一遍 
for(int k = 1; k < n; k++) 
	for(int i = 1; i < n; i++) 
		for(int j = 1; j < n; j++) 
			if(edge[i][j] > edge[i][k] + edge[k][j]) 
				edge[i][j] = edge[i][k] + edge[k][j];
			
		
		

执行上述算法后 , 邻接矩阵 中的元素值 , 就是对应的 任意两个点 之间的最小距离 ;

八、弗洛伊德算法总结

---

弗洛伊德算法 可以 计算出 图中 任意两个点 的最短路径 ;

弗洛伊德算法的 时间复杂度是 $\mathrm{O}({\mathrm{n}}^3)$ , 因为其嵌套了 3 层 for 循环 ; 结点数量小于 200 , 都可以使用该算法 ;

如果 图 中 , 边的权重 有 负数 , 并且 负数 所在边 与其它的边 组成了一个环 , 则不能使用 弗洛伊德算法 处理 ;

负环示例 :