FM算法详解
Posted bitcarmanlee
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了FM算法详解相关的知识,希望对你有一定的参考价值。
项目github地址:bitcarmanlee easy-algorithm-interview-and-practice
欢迎大家star,留言,一起学习进步
1.FM背景
在计算广告中,CTR预估(click-through rate)是非常重要的一个环节,因为DSP后面的出价要依赖于CTR预估的结果。在前面的相关博文中,我们已经提到了CTR中相关特征工程的做法。对于特征组合来说,业界现在通用的做法主要有两大类:FM系列与Tree系列。今天,我们就来讲讲FM算法。
2.one-hote编码带来的问题
FM(Factorization Machine)主要是为了解决数据稀疏的情况下,特征怎样组合的问题。已一个广告分类的问题为例,根据用户与广告位的一些特征,来预测用户是否会点击广告。数据如下:(本例来自美团技术团队分享的paper)
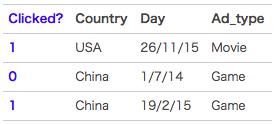
clicked是分类值,表明用户有没有点击该广告。1表示点击,0表示未点击。而country,day,ad_type则是对应的特征。前面我们在http://blog.csdn.net/bitcarmanlee/article/details/51472816一文中专门提到过,对于这种categorical特征,一般都是进行one-hot编码处理。
将上面的数据进行one-hot编码以后,就变成了下面这样

因为是categorical特征,所以经过one-hot编码以后,不可避免的样本的数据就变得很稀疏。举个非常简单的例子,假设淘宝或者京东上的item为100万,如果对item这个维度进行one-hot编码,光这一个维度数据的稀疏度就是百万分之一。由此可见,数据的稀疏性,是我们在实际应用场景中面临的一个非常常见的挑战与问题。
one-hot编码带来的另一个问题是特征空间变大。同样以上面淘宝上的item为例,将item进行one-hot编码以后,样本空间有一个categorical变为了百万维的数值特征,特征空间一下子暴增一百万。所以大厂动不动上亿维度,就是这么来的。
3.对特征进行组合
普通的线性模型,我们都是将各个特征独立考虑的,并没有考虑到特征与特征之间的相互关系。但实际上,大量的特征之间是有关联的。最简单的以电商为例,一般女性用户看化妆品服装之类的广告比较多,而男性更青睐各种球类装备。那很明显,女性这个特征与化妆品类服装类商品有很大的关联性,男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来,显然是很有意义的。
一般的线性模型为:
y
=
ω
0
+
∑
i
=
1
n
ω
i
x
i
y = \\omega_0 + \\sum_i=1^n \\omega_i x_i
y=ω0+i=1∑nωixi
从上面的式子很容易看出,一般的线性模型压根没有考虑特征间的关联。为了表述特征间的相关性,我们采用多项式模型。在多项式模型中,特征 x i x_i xi与 x j x_j xj的组合用 x i x j 表 示 x_ix_j表示 xixj表示。为了简单起见,我们讨论二阶多项式模型。具体的模型表达式如下:
y = ω 0 + ∑ i = 1 n ω i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n ω i j x i x j y = \\omega_0 + \\sum_i=1^n \\omega_i x_i + \\sum_i=1^n-1\\sum_j=i+1^n \\omega_ijx_ix_j y=ω0+i=1∑nωixi+i=1∑n−1j=i+1∑nωijxixj
上式中,
n
n
n表示样本的特征数量,
x
i
x_i
xi表示第
i
i
i个特征。
与线性模型相比,FM的模型就多了后面特征组合的部分。
4.FM求解
从上面的式子可以很容易看出,组合部分的特征相关参数共有 n ( n − 1 ) 2 \\fracn(n-1)2 2n(n−1)个。但是如第二部分所分析,在数据很稀疏的情况下,满足 x i x_i xi, x j x_j xj都不为0的情况非常少,这样将导致 ω i j \\omega_ij ωij无法通过训练得出。
为了求出 ω i j \\omega_ij ωij,我们对每一个特征分量 x i x_i xi引入辅助向量 V i = ( v i 1 , v i 2 , ⋯ , v i k ) V_i=(v_i1,v_i2,\\cdots,v_ik) Vi=(vi1,vi2,⋯,vik)。然后,利用 v i v j T v_iv_j^T vivjT对 ω i j \\omega_ij ωij进行求解。

那么
ω
i
j
\\omega_ij
ωij组成的矩阵可以表示为:

上面的表达形式,就对应了一种矩阵的分解。对
k
k
k值的限定,就反应了FM模型的表达能力。
要求出
<
v
i
,
v
j
>
<v_i,v_j>
<vi,vj>,主要是采用了如公式
(
(
a
+
b
+
c
)
2
−
a
2
−
b
2
−
c
2
((a+b+c)^2-a^2-b^2-c^2
((a+b+c)2−a2−b2−c2求出交叉项。具体过程如下: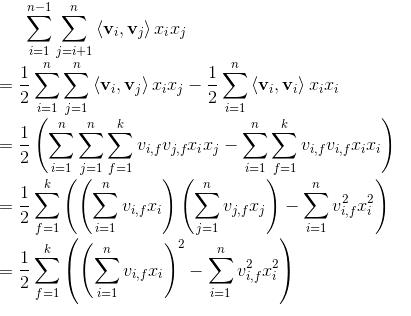
以上是关于FM算法详解的主要内容,如果未能解决你的问题,请参考以下文章