路径规划基于matlab改进的帝国企鹅算法机器人栅格地图最短路径规划含Matlab源码 2388期

Posted 2023-03-06 海神之光

⛄一、帝企鹅算法简介

目前，关于帝企鹅算法在国内外研究较少，在中对该算法进行了分析，并且与常见的粒子群算法、萤火虫算法进行了对比分析. 帝企鹅从事各种活动，如狩猎、群体觅食，是群居性动物.每当恶劣的气候来临，它们会挤在一起防风御寒.帝企鹅在南极极端冬季期间主要以集群的方式互相取暖来度过−40 ℃ 的冬季. 为了保证每只企鹅都能取暖，因此每只企鹅都在平等地做出贡献，同时它们的社交行为极为团结以及分工明确. 集群的行为可归纳如下.
1 确定集群边界范围　
设定在帝企鹅蜷缩取暖的过程中所选择的位置范围在多边形的网格范围内，帝企鹅在聚集的过程中至少与两只以上的帝企鹅相邻，邻居的选择是随机的；而在帝企鹅集群过程中范围的边界是不规则的多边形，因此用围绕住帝企鹅集群的风的梯度来表示整体集群的边界，在此定义风速 和其梯度 、 ，集群边界 ，可表示为
γ = ∆α, (8) µ = α+iβ. (9) W

2 计算集群层次周围的温度　
南极严酷的外界环境使得帝企鹅在迁徙过程中面对寒冷天气会采取集群取暖来保持温度. 若当前聚集半径 d>0.5 时，其温度 W=0；当 d<0.5 时，其温度 W=1. 温度梯度曲线可以描述为

其中， 为最大迭代次数，x 为当前迭代次数，温度的表达式

3 计算帝企鹅间的距离　
在集群范围内帝企鹅间的距离表示为该个体与集群中心帝企鹅的距离，集群距离公式如下：

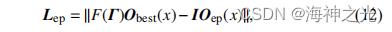
其中， 代表帝企鹅距中心距离； x 表示当前迭代数； 和 用于帝企鹅体积设置的影响向量因子，
避免个体间的冲突； 为 x 轮最优解；表示当前帝企鹅的位置向量； 定义帝企鹅的主体社会地位，负责区别最优个体与普通个体. 向量和 计算如下：

其中 ， 是移动步长参数，这里 的值设置为 2.5， 通过比较与最优的差异来定义多边形网格精度，而 是一个随机函数. 函数计算如下：

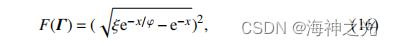
其中，ξ 和 φ是控制参数，其值分别在（2,3）（1.5,2）的范围内能得出更好的结果.

4 帝企鹅位置更新　帝企鹅集群中的个体通过向集群中心帝企鹅 Q 的方向移动更新位置信息，其位置更新如下：
Oep(x+1) = Obest(x)−ΓLep, (17)
其中，Oep(x+1)代表皇帝企鹅的下一个更新位置.在迭代过程中，一旦移动者重新定位，帝企鹅的上述参数将被重新计算.

⛄二、部分源代码

clc;
clear;
close all;
warning off

%% 固定随机数种子
noRNG=1;
rng(‘default’)
rng(noRNG)

%% 载入数据
data.numPJM=[3,5,7,9,11;
5,10,20,70,90;
3,5,7,15,19];
data.boundT=[5,10];
noPro=[1:length(data.numPJM(1,:))];
%parpool(8)
option.repeatNum=24;
%%
j=1;
%% 随机生成数据
data.sizeMap=20:20:100;
mapSize=data.sizeMap(j);
%%
data.map=rand(mapSize)<0.2;
data.S=[1,1];
data.E=[mapSize,mapSize];
data.map(data.S(1),data.S(2))=0;
data.map(data.E(1),data.E(2))=0;
[p1,p2]=find(data.map0);
data.node=[p1,p2];
data.noS=find(p1data.S(1) & p2data.S(2));
data.noE=find(p1data.E(1) & p2==data.E(2));
data.D=pdist2(data.node,data.node);
data.D1=pdist2(data.node,data.E);
[p1,p2]=find(data.D<=sqrt(2));
index=sub2ind([length(data.node(:,1)),length(data.node(:,1))],p1,p2);
data.net=[p1,p2,data.D(index)];
dim=length(index);
option.maxEfs=mapSize*1000;
%%
option.dim=dim;
lb=0;
ub=1;
option.lb=lb;
option.ub=ub;
if length(option.lb)==1
option.lb=ones(1,option.dim)*option.lb;
option.ub=ones(1,option.dim)*option.ub;
end

%option.fobj0=option.fobj;
option.showIter=0;
%% 算法参数设置 Parameters
% 基本参数
option.numAgent=100; %种群个体数

% 帝企鹅算法
option.v_lb=-(option.ub-option.lb)/4;
option.v_ub=(option.ub-option.lb)/4;
option.w2=0.5; %weight of Moving strategy III
option.w4=1;%weight of Moving strategy III
option.w5=1;%weight of Moving strategy III
option.pe=0.01; % rate to judge Premature convergence

option.gapMin=5; % min gap
option.dec=2; % dec of gap
option.L=10; % Catastrophe
%%
option.p1_GA=0.9;
option.p2_GA=0.1;
%% DE
option.F=0.5;
option.CR=0.5;
%% Imroved AFO
option.P_stratage=[0.05,0.2,0.7];
option.p=0.1;
option.alpha=10;
option.gama=1;
str_legend=[‘IAFO’];
selectedAlgorithm=[@IAFO_Final1];
data.sizeMap0=mapSize;
option.maxIteration=mapSize1000/option.numAgent; %最大迭代次数
option.maxEfs=mapSize1000;
option.dim=dim;
option.gap0=ceil(sqrt(option.maxIteration*2))+1;
lb=-ones(1,dim)*0;
ub=ones(1,dim)1;
option.lb=lb;
option.ub=ub;
%%
%% 初始化种群个体
%% 使用算法求解
for ii=1:length(selectedAlgorithm)
option.fobj=@aimFcn_PPP;
x=ones(option.numAgent,option.dim);
y=ones(option.numAgent,1);
for i=1:option.numAgent
x(i,:)=rand(size(option.lb)).(option.ub-option.lb)+option.lb;
y(i)=option.fobj(x(i,:),option,data);
end
rng(noRNG)
tic
[bestY(ii,:),bestX(ii,:),recordingii]=selectedAlgorithmii(x,y,option,data);
recordingT(ii,j)=toc;
end

⛄三、运行结果

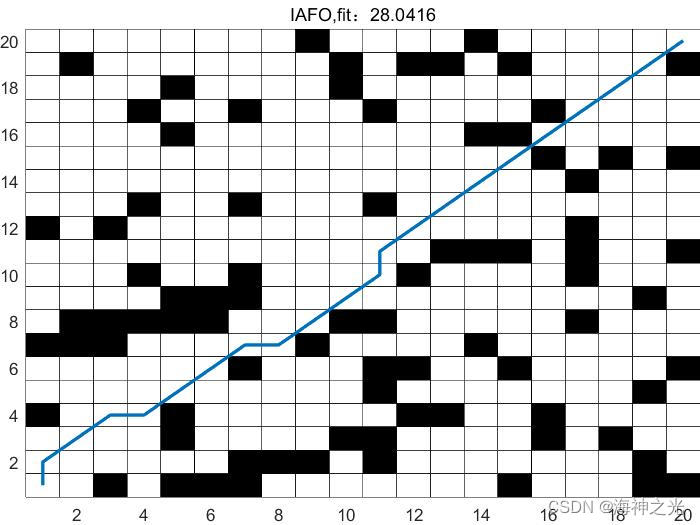
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]唐菁敏,曲文博,苏慧慧,郑锦文.一种基于帝企鹅差分算法的WSN覆盖优化[J].云南大学学报(自然科学版). 2021,43(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除