优化指派基于matlab粒子群算法求解指派优化问题（工作质量）含Matlab源码 2390期

Posted 2023-03-06 海神之光

⛄一、飞机指派模型的建立简介

1 飞机指派问题概述
飞机排班是依据航空公司的航班计划和飞机维护工作安排为每一个航班指定一架具体执行的飞机, 也即给每一个航班号分配一个相应的机尾号。目前, 国内航空公司的飞机排班流程大致如下:

1)根据航空公司的航班时刻表,将航空公司一个周期内所有航班连接成时间地点前后衔接的航班串。
2)将生成的航班串进行筛选,得到覆盖所有航班而且满足一定目标的部分航班串。这里的“一定目标” 一般是指航班串数最少。航班串数越少在随后的指派过程中用到的飞机就越少。
3)为筛选得到的每一个航班串指派一架具体执飞的飞机。
飞机排班的过程中要受到航班飞行区域、飞机维修计划等诸多因素的制约,本文针对上述飞机排班问题中的第3个子问题进行研究,主要考虑的约束如下:
1)唯一性约束在同一时间每架飞机最多只能执行一个航班,每个航班只能由一架飞机执行。
2)飞机总数约束任何时刻在地面机场的飞机数和在空中执行航班的飞机数之和保持不变。
3)飞机与航班的匹配性约束飞机的大小、可飞行区域等要与航班要求相一致。

2 飞机指派问题优化模型
飞机指派优化问题涉及问题规模较大,变量众多,本文基于以上约束,建立了以成本最小化为目标函数的飞机指派模型。模型符号和参数的具体说明如下:

式(1)是成本最小化的目标函数;式(2)和式(3) 是唯一性约束,式(2)表示排班结果应保证每一个航班有且只有一架飞机执行,式(3)表示同一时间每架飞机最多只能执行一个航班;式(4)和式(5)为飞机数量守恒约束,式(4)表示在任意时刻t,在空中执行航班的飞机数量与在地面机场的飞机数量之和等于在排班方案中用到的飞机总数,式(5)表示机场飞机数量守恒,即对任一机场o(o∈S),在任意时刻t从其他机场飞抵机场o的飞机数量与从t-到t时刻一直在机场o的飞机数量之和,等于t时刻从o机场飞往其他机场的飞机数量与t到t+留在o机场的飞机数量之和;式(6)为飞机总数约束,在排班方案中用到的飞机总数不能大于航空公司的可用飞机总数;式(7)表示对于任意时刻t,机场o(o∈S)的飞机数量不能为负。

⛄二、部分源代码

      %==参数输入===========================================

%swarminitnum粒子数，gen循环代数，w1变异率。
swarminitnum=50;
gen=300;
w1=0.35;
T=1000;
man=[0.00 0.00 0.00 0.86 0.00 0.91 0.74 0.78 0.00 0.00 0.00 0.00 0.58 0.00 0.00 0.00 0.00 0.00 0.84 0.00 0.84 0.00 0.00 0.91 0.68 0.00
0.81 0.00 0.00 0.00 0.64 0.00 0.00 0.00 0.76 0.00 0.00 0.00 0.00 0.78 0.00 0.00 0.92 0.00 0.00 0.00 0.00 0.00 0.75 0.87 0.00 0.85
0.00 0.65 0.00 0.00 0.00 0.00 0.86 0.00 0.00 0.00 0.76 0.00 0.91 0.00 0.00 0.92 0.00 0.00 0.00 0.90 0.79 0.00 0.00 0.00 0.00 0.00
0.91 0.00 0.96 0.00 0.80 0.00 0.00 0.00 0.87 0.00 0.00 0.61 0.00 0.69 0.90 0.00 0.00 0.00 0.00 0.81 0.00 0.80 0.00 0.00 0.93 0.00
0.00 0.00 0.00 0.00 0.00 0.72 0.00 0.00 0.00 0.74 0.00 0.00 0.93 0.00 0.00 0.00 0.91 0.00 0.00 0.71 0.00 0.00 0.00 0.70 0.00 0.88
0.00 0.67 0.00 0.00 0.00 0.00 0.67 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.70 0.00 0.00 0.83 0.00 0.00 0.00 0.92 0.00 0.00 0.75 0.00
0.78 0.00 0.86 0.00 0.00 0.00 0.87 0.00 0.00 0.85 0.00 0.00 0.00 0.00 0.88 0.00 0.84 0.91 0.00 0.88 0.00 0.00 0.00 0.86 0.00 0.00
0.00 0.00 0.00 0.87 0.70 0.00 0.00 0.86 0.00 0.00 0.87 0.00 0.63 0.00 0.00 0.00 0.00 0.00 0.91 0.00 0.00 0.00 0.00 0.00 0.00 0.85];
MM=[1 1 2 2 3 4 5 5 5 5 6 6 7 8 9 9 10 11 12 13 13 14 15 16 17 18 19 19 20 21 22 23 24 25
2 18 3 6 4 5 10 11 12 13 7 8 9 9 13 16 15 14 14 14 16 15 25 17 25 19 20 22 21 24 23 24 25 26];
time=[12 11 13 6 10 7 7 8 14 15 10 9 12 4 8 5 7 15 17 10 12 11 11 10 9 10];
%%随机生成初始粒子群体====================
swarminit=cell(1,swarminitnum);
for i=1:swarminitnum,
swarminiti=random(man);
end
%===========================================
[popu,s] = size(swarminit);
[en,n]=size(man);
tracee = ones(1,gen);
tracee(1) = 10000000; % 初始全局最佳适应度设为足够大
for i = 1:s,
bestfit(i) = 10000000; % 初始个体历史最佳适应度设为足够大
end
bestpar = swarminit; % 个体历史最佳粒子初始化
for l=1:swarminitnum,
fitlist(l)=[0];
end
dd1=clock;
%开始世代循环=============================
for step=1:gen,
for q=1:swarminitnum,
for pop=1:n,
time1(pop)=man(swarminitq(pop),pop);
end
fitlist(q)=uncode(MM,n,time1,swarminitq,en);
end% 计算当前粒子群每个粒子的适应度
[minval,sub] = min(fitlist); % 求得这代粒子的适应度最小值及其下标
if(tracee(step) > minval),
tracee(step) = minval;
bestparticle = swarminitsub;
end
if(step~= gen) ,
tracee(step+1)=tracee(step);% 全局最佳适应度及最佳粒子调整
end
% for i = 1:s,
% if(bestfit(i) > fitlist(i)),
T=0.95*T;
for i = 1:s,
tt=fitlist(i)-bestfit(i);
if (bestfit(i) > fitlist(i))|(min(1,exp(-tt/T))>=rand(1,1)) ,
bestfit(i) = fitlist(i);
bestpari = swarminiti;
end

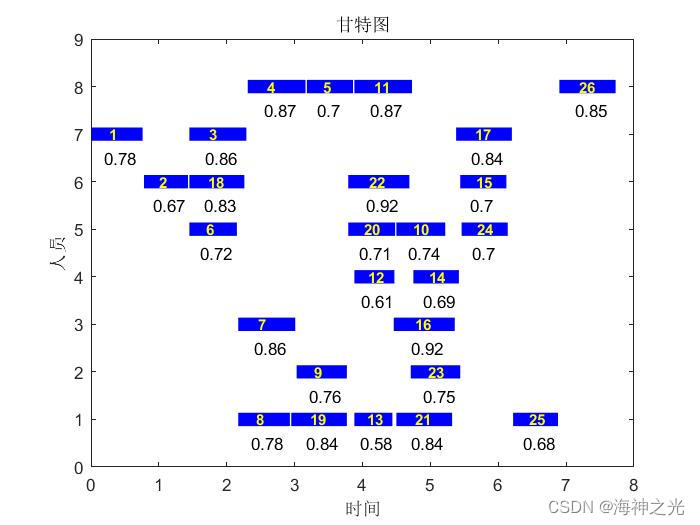
⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]贾宝惠,逯艳华,李耀华.基于交叉粒子群算法的飞机指派问题研究[J].中国民航大学学报. 2015,33(04)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除