红黑树的原理+实现

Posted 2023-03-04 正义的伙伴啊

文章目录

• 红黑树
• • 定义
  • 性质
  • 红黑树的插入
  • 动态效果演示
• 代码
• 测试红黑树

红黑树

定义

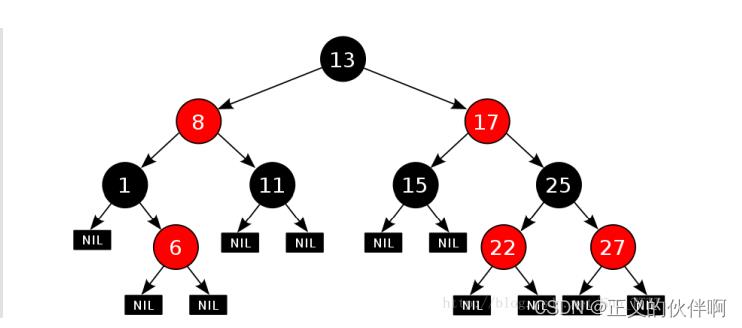
红黑树是一个近似平衡的搜索树，关于近似平衡主要体现在最长路径小于最短路径的两倍（我认为这是红黑树核心原则），为了达到这个原则，红黑树所有节点都增加了一个存储位表示节点的颜色（红或黑），并规定了一些性质来达到“近似平衡”

性质

1. 每个节点不是红色就是黑色
2. 根节点时黑色
3. 如果一个节点是红色，则它的两个孩子节点是黑色
4. 对于每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点
5. 每个叶子节点都是黑色的（空节点也算为叶子节点）

对于这些性质有一些推论：

• 红色节点的父节点一定是黑色节点
• 何时红黑树的路径最短？——该树所有节点都是黑色
• 何时红黑树的路径最长？——该树红色节点和黑色节点交替

红黑树的插入

插入之前我们首先要搞明白一个问题，插入的节点默认应该应该是什么颜色（然后根据插入后调整）？

---

插入的节点如果都设置为黑色，一定会违反性质4,。如果插入的是红色节点，分为两种情况：如果插入节点的父节点为黑色，则不需要调整，如果插入节点的父节点为红色，则需要进一步调整。
从上可知，如果默认插入的是黑色100%需要调整，而默认插入的是红色，则有50%需要调整，所以我们这里选择默认插入红色节点

红黑树的插入需要记住三种需要调整的特殊情况：下面所有情况中 cur 为当前插入后违反红黑树规则的节点，

---

• 情况一： cur和parent为红，grandparent为黑，uncle存在且为红
  
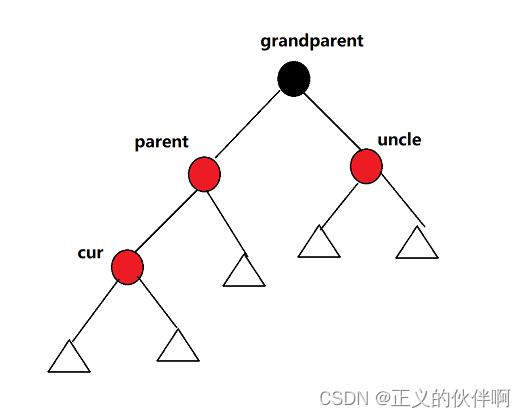
  这种情况不需要旋转只需要调整节点的颜色即可，将parent 和uncle变成黑色，grandparent变成红色（这里有特殊情况，如果grandparent为根节点时）
  
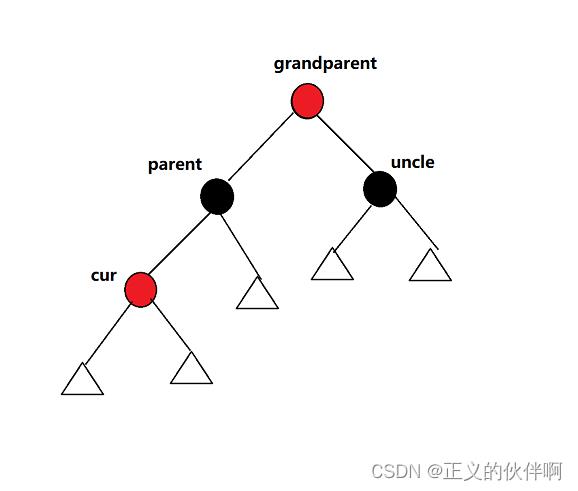
  ok到这里我们观察一下，grandparent为红色，如果grandparent的父节点为红色（因为grandparent原本为黑色，所以其父节点有可能为红色）则又会出现两个连续的红色，所以情况一结束后还要继续向上检查，这时我们将cur=grandparent继续向上遍历，继续分析下一层的情况
  

---

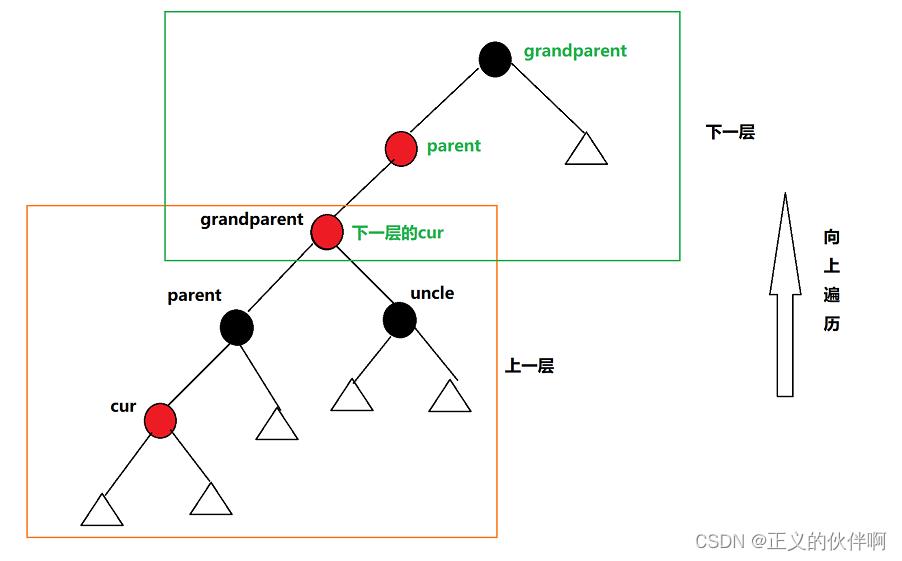
• 情况二：cur和parent为红，grandparent为黑，uncle为黑/不存在
  
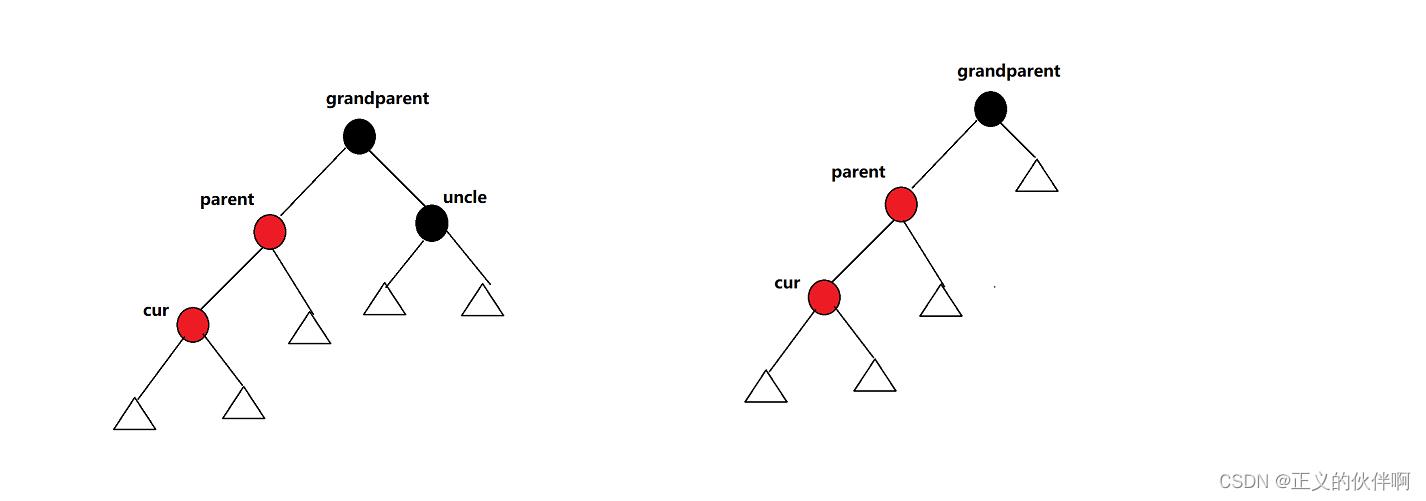
  这里有两种小情况我们先逐一分析，但是这两种小情况最后的操作都是一样的
  • uncle不存在：cur一定为新插入的节点而不是整个向上调整循环中的一次，因为如果cur不是新插入的节点，则cur或parent一定有一个是黑色，分别是从上一层的情况一和情况三变过来的，但是这就不满足红黑树的定义了。所以cur一定是新插入的节点
  • uncle存在且为黑：那么cur一定是黑色的，现在是红色是因为上一层结束后改成了红色，继续向上遍历的结果
    如何处理情况二？——右单旋+调整颜色
    
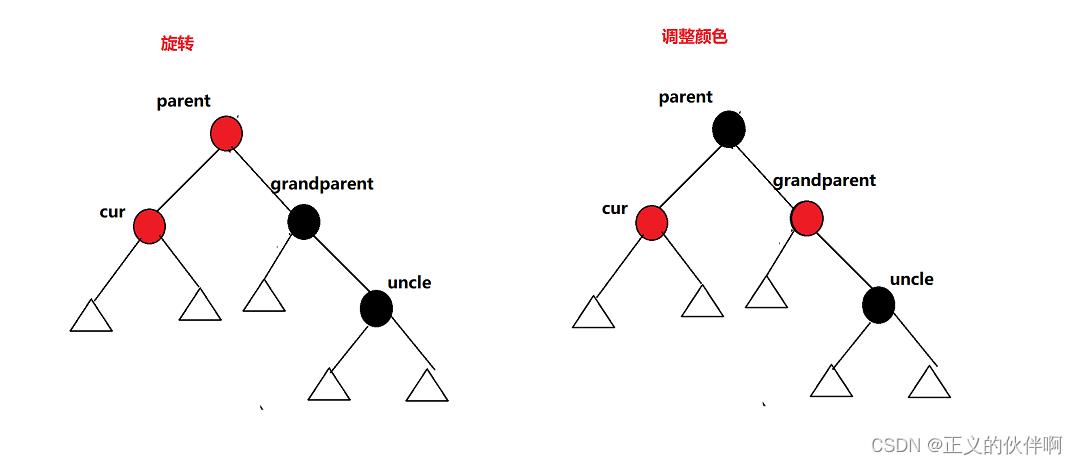
    ok到这里情况二调整完毕了。是否需要继续向上调整了？答案是不用！因为整个局部的子树调整完的根节点变成黑色了，并不会和其父节点的颜色发生冲突，所以在 整个三个情况中只要调整完之后的根节点变成了黑色，就不用向上遍历了

---

• 情况三：cur和parent为红，grandparent为黑，uncle为黑/不存在，但是cur为parent的右节点
  
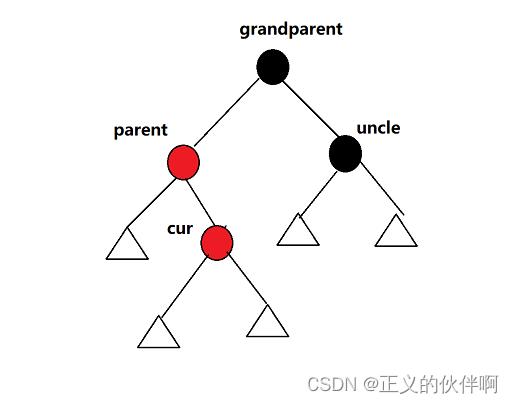
  如何处理情况三？——局部旋转！+ 转换情况二
  
  这时旋转完之后的树是不是很眼熟？就是情况二，只需要交换一下cur和parent指针的执行进入下一次的循环即可。
  这里还有另外一个思路就是：局部旋转之后直接执行情况二的右单旋，最后直接break跳出循环。两者思路其实是一模一样的

动态效果演示

以升序插入

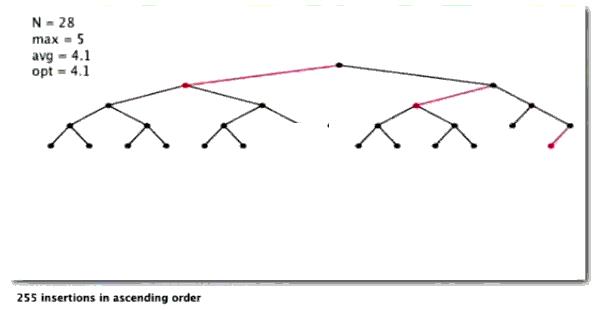
以降序插入

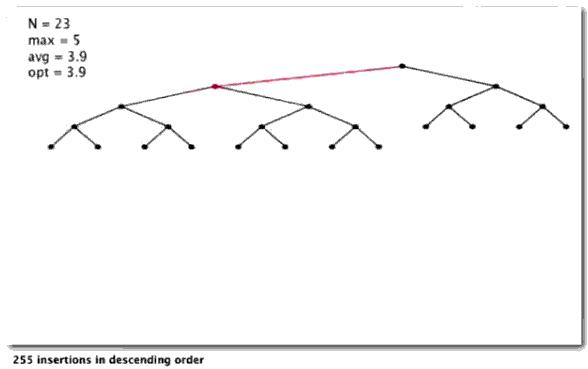
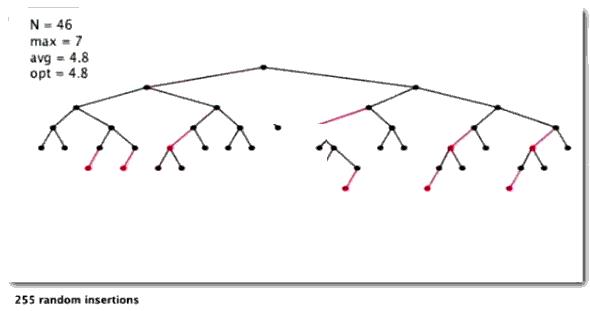
随机插入

代码

代码仓库

测试红黑树

为了测试我们写出来的红黑树是否符合要求，我们可以写一个isbalance函数，主要判断：

1. 不能出现连续的红色节点
2. 每条路径的黑色节点是否相同

两个条件分别使用不同的函数判断

具体代码实现如下：

 bool parent_isRed(Node *root) // 判断红色节点的父节点是不是黑色节点
        
            if (root == nullptr)
            
                return true;
            

            if (root->_col == RED && root->_parent->_col == RED)
            
                return false;
            

            return parent_isRed(root->_left) && parent_isRed(root->_right);
        

        void black_num_is_same(Node *root, std::vector<int> &num, int k = 0) // num存储了每条路径黑色节点的数量
        
            if (root == nullptr)
            
                num.push_back(k);
                return;
            

            if (root->_col == BLACK)
            
                k++;
            

            black_num_is_same(root->_left, num, k);
            black_num_is_same(root->_right, num, k);
        
void IsBalnace() // 检查红黑树是否平衡
        
            bool is = parent_isRed(_root);

            std::vector<int> num;

            black_num_is_same(_root, num);

            bool it = true;
            int first = num[0];
            for (const auto &e : num)
            
                if (e != first)
                
                    it = false;
                    break;
                
            

            if (it && is)
            
                std::cout << "it is a redblackTree" << std::endl;
            
            else
            
                std::cout << "it is not a redblackTree" << std::endl;
            
        

检测函数写完我们取1000个随机数向红黑树插入，并用isblance 检查是否平衡：
测试代码
输出结果：