算法思考Radial basis function interpolation （RBF）插值法

Posted 2023-03-03 Kross Sun

目录

• 什么是插值
• 什么是 Radial basis function
• 如何基于 Radial basis function 中建立插值
• • 计算插值的权重
  • 基于插值权重求解新采样点函数值
  • 代码实现
• 参考文献

什么是插值

假设我们有n个采样点，这些采样点的维度都是 k 维的, 记做 $\mathbf{X}={\mathbf{x}}_1,{\mathbf{x}}_2,\cdots {\mathbf{x}}_{\mathbf{n}}$, 对于每个 ${\mathbf{x}}_{\mathbf{i}}$ 都对应一个函数值 $y_i$ 。如果给一个新的采样点 $\mathbf{x}\notin \mathbf{X}$, 如何计算或估计出其对应的函数值 $y$, 就是插值要解决的问题。有时候我们也会遇到 $y$ 是一个向量的情况，不过可以通过建立多个插值函数来解决这个问题。

如果采样点 ${\mathbf{x}}_{\mathbf{i}}$ 都是 1 维的，我们可以采样一种非常简单的方式，即分段线性进行建模。下面举个例子：

我们有采样点 $x_0=0,y_0=0,x_1=1,y_1=1$, 可以建模为 $y=\frac{|x-x_0|}{|x-x_0|+|x-x_1|}\ast y_0+\frac{|x-x_1|}{|x-x_0|+|x-x_1|}\ast y_1$ 。当给定 $x=0.2$ 时，我们利用以上的插值函数， 可以计算出来 $y=0.2$ 。

观察上面建立的模型，我们可以总结出插值近似于在点集之间根据距离关系建立不同的权重，按照权重累加得到目标值。
由此，可以总结一个一般形式的插值函数表示：
$$\bar{f}(\mathbf{x})=\sum _i^n{\omega }_i\psi (||\mathbf{x}-{\mathbf{x}}_i||)\times y_i\text{\hspace{1em}(1)}$$
其中$\psi ()$是一个Radial basis function。

什么是 Radial basis function

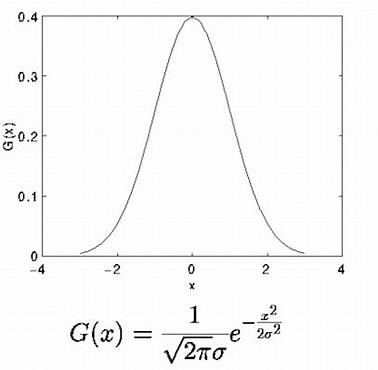
Radial basis function 是一个只和距离$r$有关的函数，距离越近时函数值越大，距离越远时函数值越小。常见的 Radial basis function 函数如:

$$f(r)=\frac{1}{\sigma \sqrt{2\pi }}\exp (-\frac{r^2}{2{\sigma }^2})$$

函数图像为：

如何基于 Radial basis function 中建立插值

计算插值的权重

如果提供了 $\mathbf{X}={\mathbf{x}}_1,{\mathbf{x}}_2,\cdots {\mathbf{x}}_{\mathbf{n}},\mathbf{y}=y_1,y_2,\cdots y_n$。我们要求在采样点需要做到精确拟合，也就是$\bar{f}({\mathbf{x}}_{\mathbf{i}})=y_i$那么结合(1)我们知道以下式子成立
$$\bar{f}({\mathbf{x}}_j)=\sum _i^n{\omega }_i\psi (||{\mathbf{x}}_j-{\mathbf{x}}_i||)\times y_i=y_j$$
因此可以构造出 $n$ 个上述等式，如果我们确定了 radial basis function, 可以将$\psi (||{\mathbf{x}}_i-{\mathbf{x}}_j||)$ 记作 ${\psi }_{i,j}$ 是已知量。由此可以得到：
( ψ 1 , 1 ψ 1 , 2 ⋯ ψ 1 , n ⋮ ⋮ ⋮ ψ n , 1 ψ n , 2 ⋯ ψ n , n ) ( w 1 w 2 ⋮ w n ) = ( y 1 y 2 ⋮