速通版吴恩达机器学习笔记Part3

Posted 2023-03-02 ViviranZ

目录

1.多元线性回归

a.特征缩放

 可行的缩放方式：

1.除以最大值：

 2.mean normalization：

 3.Z-score normalization

b.learning curve:

 c.learning rate:

2.多项式回归

3.classification

 logistics regression

---

1.多元线性回归

其意义很清晰了，多维更准确。很有意思也是我之前没关注的点是，一般下标表示分量、上标表示不同的inputs、又为了区分次数加了括号。

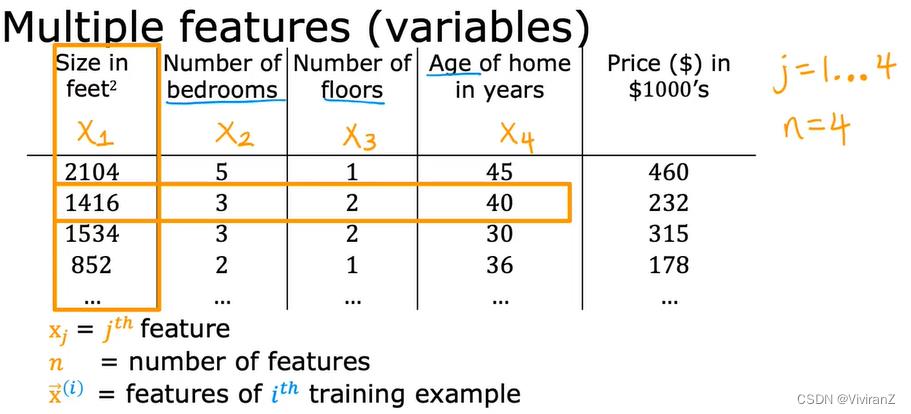
点乘是np.dot

用向量化的函数而不是分量循环，可以提高效率。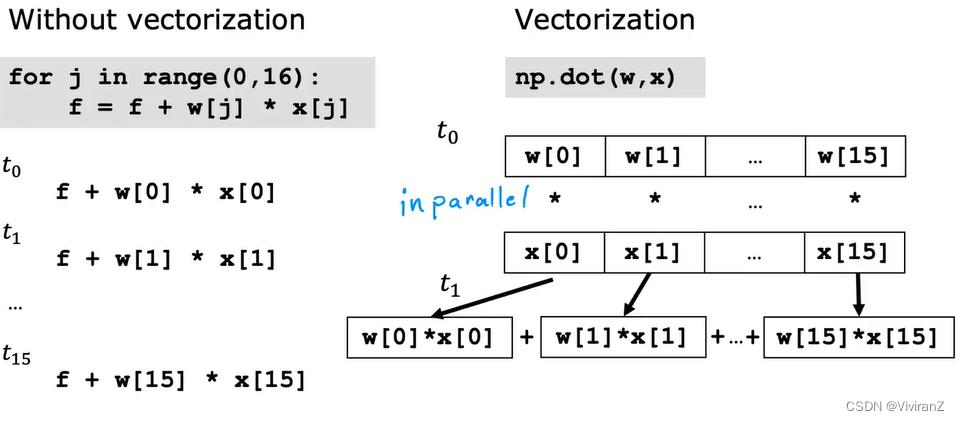

  讲真矢量化和parallel真的好酷呀……作为数学专业我理解是从notation的角度，很清晰很明确，但是从算法编程的角度也有其优势、而这样的优势是由底层代码包的编写者、底层（非judge义）工程师实现的。这也算是某种意义下的殊途同归吧。

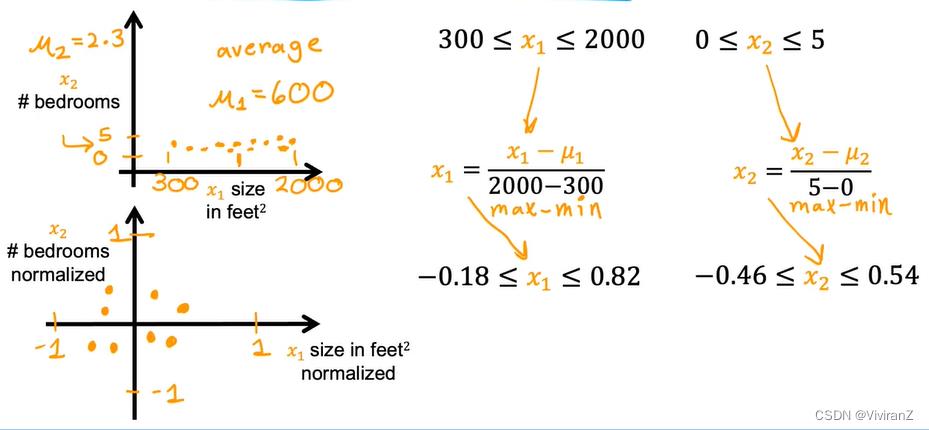
a.特征缩放

 以房价为例，相关因素考虑大小和卧室数量，可以看到大小数值非常大，那么调整w的时候可能会很困难，因为w可能只是变了一点点，wx就变了非常大，因此考虑调整范围差不多

 

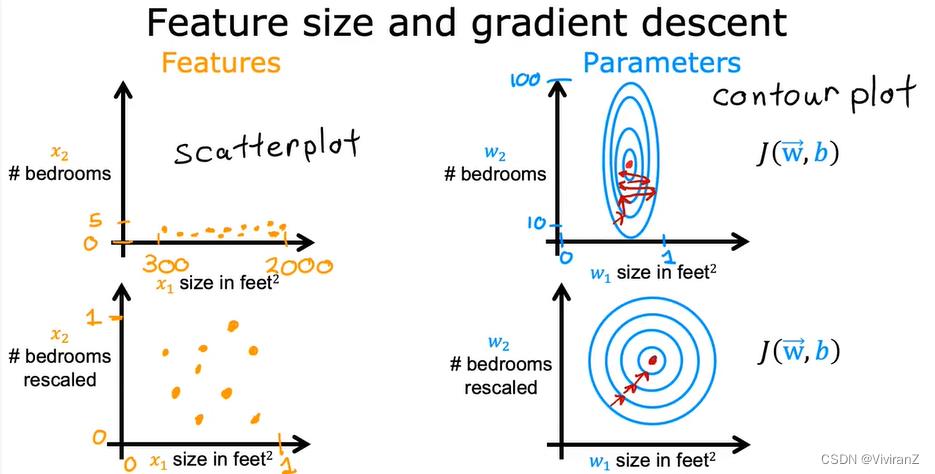
 可行的缩放方式：

1.除以最大值：

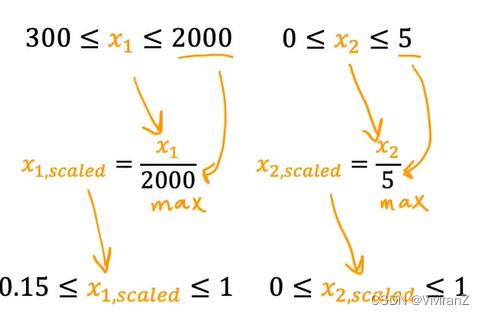
 2.mean normalization：

 3.Z-score normalization

 

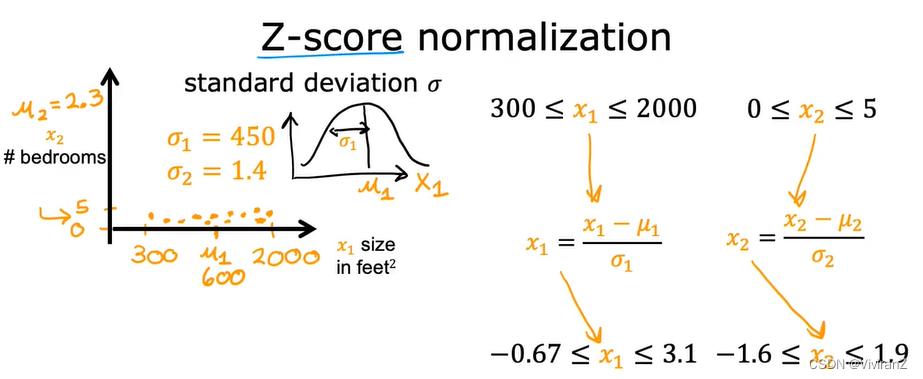
霍，还需要多次缩放呢。。。。

b.learning curve:

标注了随着迭代次数的增加目标函数的变化，（比设置\\epsilon更直观） 

 c.learning rate:

通常来说，在learning curve里可能出现随着迭代次数的增加，loss function震荡甚至上升，这可能由于 1.BUG 2.学习率过大，因此可调试中尝试设置很小的学习率，如果正常会下降的。但是，实际学习的过程中学习率不能太小，这样效率太低。 

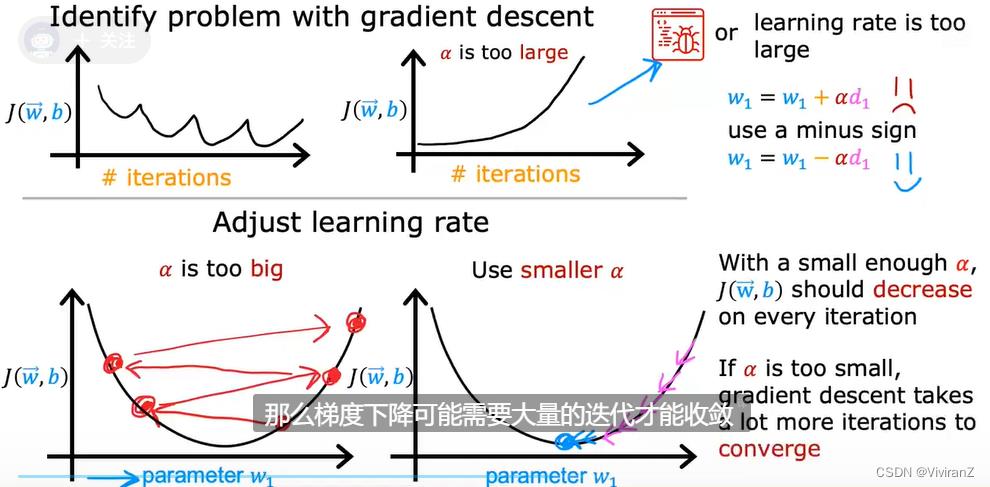
大佬常用方法：先设置很小的学习率跑几个epoch，，然后3倍3倍增加，保证找到过小（下降很慢）和过大（震荡或者上升），然后在合适范围内找尽量大的。

 2.多项式回归

 简单来说，就是线性不合适啦，我们想自己选选用高次、乘积、开根等不同方法~不赘述

3.classification

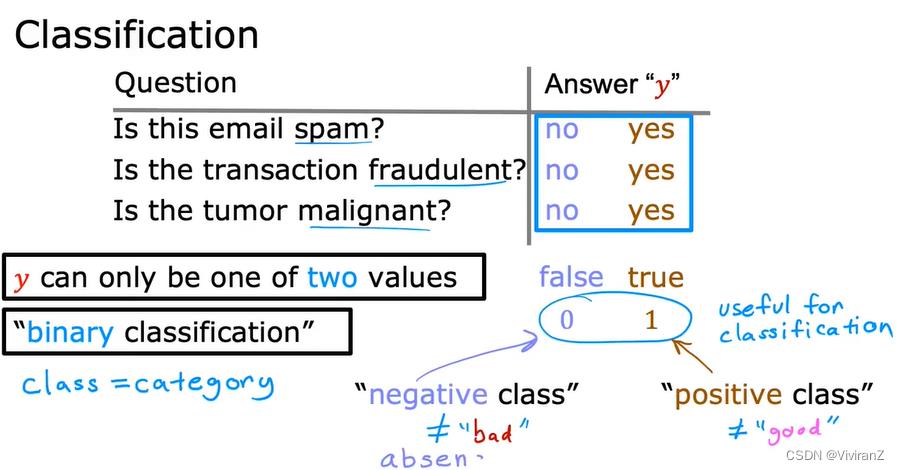
 正如以下例子可以看到，拟合有时候很差：本来考虑左侧的四个negative class和positive class，设置阈值threshold为0.5，效果就很好了，但是当我们加入最右的例子，本来是一个一看就是positive sample的例子，但是却导致预测结果出现偏差。因此我们考虑classification。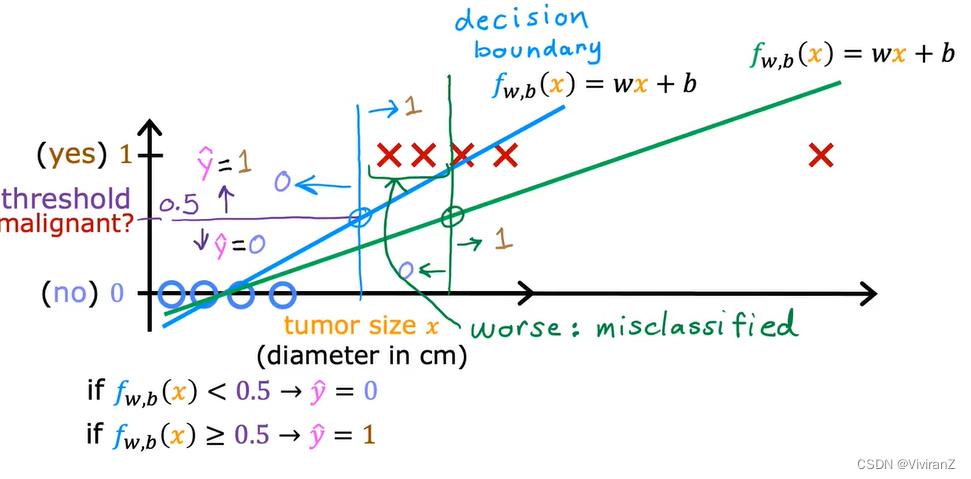

 logistics regression

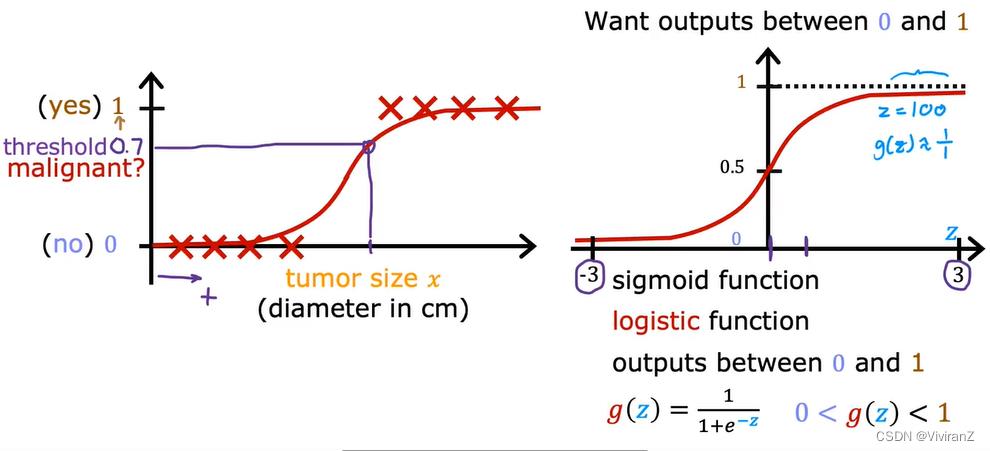
可以看出，非常满足的例子在逻辑斯蒂回归里尽量不重视，而在中间的样本更加强调。怎么强调呢，也就是说，当我们多发现中部模糊地带的样本，对threshold的影响很剧烈、也就是拟合函数中斜率很大。 

重述一下，我们在线性之外拟合一个逻辑斯蒂回归来做分类，就是为了防止【本来很明确分类的样本加进去反而会影响算法的输出结果】，让算法更关注于模糊地带的样本。f输出的可以理解为【样本特征为x的情况下，分类为1的概率】。

 

 可视化理解，略过 

logistics regression-Cost function:

在线性回归中 平方误差很好用（凸的，可以直接到达全局最优），但是逻辑斯蒂回归模型平方误差就是非凸了，因此我们考虑换一个cost。

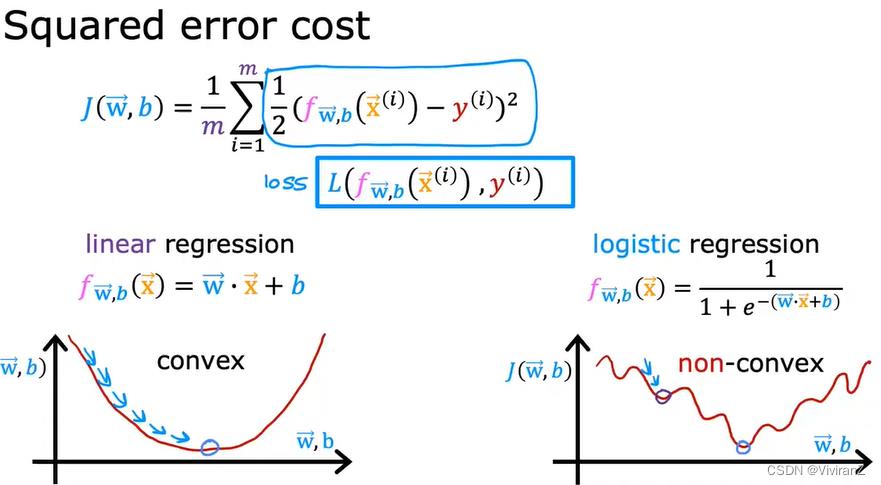
 因此，转而用以下的函数：

值得注意的是，此处的函数是分类函数。那么目标函数转化为：

 利用梯度下降法：

 GD实现，逻辑斯蒂回归模型与线性回归函数不同但是trick类似