ARIMA时间序列预测MATLAB代码模板(无需调试)
Posted 噢⊙▽⊙
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ARIMA时间序列预测MATLAB代码模板(无需调试)相关的知识,希望对你有一定的参考价值。
小白专用,直接改成自己的数据运行即可完成预测并画图
我的数据在评论区自取,
clear; clc
%小白专用,"*********《需要自己输入》**********"仅在有这种注释的地方改成自己的数据即可,一共有4个地方
DD=readmatrix("B.xlsx");%这里输入自己的单序列数据,要求行向量*********《需要自己输入》**********
P=DD(1:500,2)';
N=length(P);
n=490;%自己选取训练集个数*********《需要自己输入》**********
F = P(1:n+2);
%----------------------由于时间序列有不平稳趋势,进行两次差分运算,消除趋势性----------------------%
Yt=[0,diff(P,1)];
L=diff(P,2);%全体,比原始数据少2个,因为做了差分
Y=L(1:n); %输入
a=length(L)-length(Y);%单步预测步数
aa=a;%多步预测步数
% %画图
% figure;
% plot(P);
% title('原数据序列图');
% hold on;
% figure;
% plot(Y,'*');
% title('两次差分后的序列图和原数对比图');
%%
%--------------------------------------对数据标准化处理----------------------------------------------%
%处理的算法 : (data - 期望)/方差
Ux=sum(Y)/n ; % 求序列均值
yt=Y-Ux;
b=0;
for i=1:n
b=yt(i)^2/n+b;
end
v=sqrt(b); % 求序列方差
% Y=yt/v; % 标准化处理公式
Y=zscore(Y);
f=F(1:n);
t=1:n;
%画图
% figure;
% plot(t,f,t,Y,'r')
% title('原始数据和标准化处理后对比图');
% xlabel('时间t'),ylabel('油价y');
% legend('原始数据 F ','标准化后数据Y ',"Location","best");
%%
%--------------------------------------对数据标准化处理----------------------------------------------%
%------------------------检验预处理后的数据是否符合AR建模要求,计算自相关和偏相关系数---------------%
%---------------------------------------计算自相关系数-----------------------------------%
%%
R0=0;
for i=1:n
R0=Y(i)^2/n+R0; %标准化处理后的数据的方差
end
for k=1:20
%R 协方差
R(k)=0;
for i=k+1:n
R(k)=Y(i)*Y(i-k)/n+R(k);
end
end
x=R/R0 ; %自相关系数x = 协方差/方差
%画图
% figure;
% plot(x)
% title('自相关系数分析图');
%%
%-----------------------------------计算自相关系数-------------------------------------%
%-----------------------解Y-W方程,其系数矩阵是Toeplitz矩阵(多普里兹矩阵)。求得偏相关函数X-------------------
X1=x(1);xx(1,1)=1;X(1,1)=x(1);B(1,1)=x(1);
K=0;T=X1;
for t=2:n
at=Y(t)-T(1)*Y(t-1);
K=(at)^2+K;
end
U(1)=K/(n-1) ; % 1阶模型残差方差
for i =1:19
B(i+1,1)=x(i+1);
xx(1,i+1)=x(i);
A=toeplitz(xx);
XX=A\\B; %x=a\\b是方程a*x =b的解
XXX=XX(i+1);
X(1,i+1)=XXX;
K=0;T=XX;
for t=i+2:n
r=0;
for j=1:i+1
r=T(j)*Y(t-j)+r;
end
at= Y(t)-r;
K=(at)^2+K;
end
U(i+1)=K/(n-i+1); %计算20阶以内的模型残差方差
end
%-----------------------------------解Y-W方程,得偏相关函数X-------------------------------------%
% figure;
% plot(X);
% title('偏相关函数图');%自己要根据图先判断阶次
%%
q=20;%猜测阶数,通过看上面偏相关图,*********《需要自己输入》**********
%-----根据偏相关函数截尾性,初判模型阶次为5。用最小二乘法估计参数,计算20阶以内的模型残差方差和AIC值,应用AIC准则为模型定阶--%
S(1,1)=R0;
for i = 1:q-1
S(1,i+1)=R(i);
end
G=toeplitz(S);
%inv(G)返回G的反函数
W=inv(G)*[R(1:q)]' ; % 参数W(i) 与X5相同 G*W = [R(1:5)]'
U=20*U ;
for i=1:20
AIC2(i)=n*log(U(i))+2*(i) ;
end
% 比如AIC2值为:172.6632 165.4660 153.2087 145.1442 140.7898 141.6824 142.9944 144.5601 146.3067 148.7036
%-----------------取使AIC值为最小值的阶次,判断模型阶次为5。用最小二乘法估计参数--------------------%
%%
q=20;%确定阶数 ,通过看AIC2值最小的位置,*********《需要自己输入》**********
%------------------检验at是否为白噪声。求at的自相关系数,看其是否趋近于零-----------------------%
C=0;K=0;
for t=q+2:n
at=Y(t)+Y(q+1);
for i=1:q
at=-W(i)*Y(t-i)-W(i)*Y(q-i+1)+at;
end
at1=Y(t-1);
for i=1:q
at1=-W(i)*Y(t-i-1)+at1;
end
%at1=Y(t-1)-W(1)*Y(t-2)-W(2)*Y(t-3)-W(3)*Y(t-4)-W(4)*Y(t-5)-W(5)*Y(t-6);
C=at*at1+C;
K=(at)^2+K;
end
p=C/K ; %若p接近于零,则at可看作是白噪声
%--------------------------------at的自相关系数,趋近于零,模型适用---------%
%%
%------------AR(5)模型方程为-----------------------------------------------%
% X(t)=W(1)*X(t-1)-W(2)*X(t-2)-W(3)*X(t-3)-W(4)*X(t-4)-W(5)*X(t-5)+at
%------------------------------------------后六年的数据 进行预测和效果检验------------------------------------%
%注意注意注意a为测试集的元素个数
%-----------------------------单步预测 预测当前时刻后的a个数据---------------%
XT=[L(n-q+1:n+a)];
for t=q+1:q+a
m(t)=0;
for i=1:q
m(t)=W(i)*XT(t-i)+m(t);
end
end
m=m(q+1:q+a);
%-------------预测值进行反处理---------------%
for i =1:a
m(i)=Yt(n+i+1)+m(i); %一次反差分
z1(i)=P(n+i+1)+m(i);%二次反差分
end
% z1 ; % 单步预测的向后6个预测值
%---------------------------绘制数据模型逼近曲线----------------------------%
for t=q+1:n
r=0;
for i=1:q
r=W(i)*Y(t-i)+r;
end
at= Y(t)-r;
end
figure;
for t=q+1:n
y(t)=0;
for i=1:q
y(t)=W(i)*Y(t-i)+y(t);
end
y(t)=y(t)+at;
y(t)=Yt(t+1)-y(t);
y(t)=P(t+1)-y(t); %反差分的过程
end
plot(y,'r.'); % 样本数据模型逼近曲线
hold on;
plot(n+2:n+a+1,z1,'r-*'); %向后a布预测
hold on;
plot(P,"--"); % 原样本曲线
title('AR(q)模型样本逼近预测曲线');
legend("训练样本预测值","测试集预测值","真实值","Location","best");
%-------------------------检测单步预测误差
D_a=P(n+2:end-1);
for i=1:a
e6_a(i)=D_a(i)-z1(i);
PE6_a(i)= (e6_a(i)/D_a(i))*100;
end
e6_a; % 多步预测的绝对误差
PE6_a; % 多步预测的相对误差
1-abs(PE6_a); % 准确率
%------多步预测平均绝对误差
mae6_a=sum(abs(e6_a)) /6 ;
%------多步预测平均绝对百分比误差
MAPE6_a=sum(abs(PE6_a))/6
%------绘制预测结果和实际值的比较图
figure;
plot(1:a,D_a,'-+')
hold on;
plot(z1,'r-*');
title('单步,向后a步预测值和实际值对比图');
legend("真实值","预测值","Location","best");
hold off;
%%
%-----------------------------绘制数据模型逼近曲线--------------------------%
%-------------------------预测误差分析(多步)------------------------%
%----------------------------------多步预测 目的是向后aa步预测--------------%
Z(1)=0;Xt=0;
for i =1:q
Xt(1,i)=Y(n-q+i);
end
%Xt=[ Y(n-4) Y(n-3) Y(n-2) Y(n-1) Y(n)]; %取当前时刻之前的q个数据
for i =1:q
Z(1)=W(i)*Xt(q-i+1)+Z(1);
end
%Z(1)=W(1)*Xt(5)+W(2)*Xt(4)+W(3)*Xt(3)-W(4)*Xt(2)-W(5)*Xt(1) ;
%------求向前l步的预测值
%预测步数小于q时
for l=2:q
K(l)=0;
for i=1:l-1
K(l)=W(i)*Z(l-i)+K(l);
end
G(l)=0;
for j=l:q
G(l)=W(j)*Xt(q+l-j)+G(l);
end
Z(l)=K(l)+G(l);
end
%预测步数大于q时(向前aa步预测)
for l=q+1:aa
K(l)=0;
for i=1:q
K(l)=W(i)*Z(l-i)+K(l);
end
Z(l)=K(l);
end
%----预测值进行反标准化处理
r=Z*v+Ux ;
r(1)=Yt(n+2)+r(1); %一次反差分
z(1)=P(n+2)+r(1) ; %二次反差分
for i=2:aa
r(i)=r(i-1)+r(i);
z(i)=z(i-1)+r(i) ;
end
%%
%---------------------------- 预测误差分析 ------------------------------%
%-------计算绝对误差和相对误差
D=P(n+2:end-1);
for i=1:aa
e6(i)=D(i)-z(i);
PE6(i)= (e6(i)/D(i))*100;
end
e6 ; % 多步预测的绝对误差
PE6 ; % 多步预测的相对误差
1-abs(PE6) ; % 准确率
%------多步预测平均绝对误差
mae6=sum(abs(e6)) /6 ;
%------多步预测平均绝对百分比误差
MAPE6=sum(abs(PE6))/6
%------绘制预测结果和实际值的比较图
figure;
plot(1:aa,D,'-+')
hold on;
plot(z,'r-*');
title('多步,向后aa步预测值和实际值对比图');
legend("真实值","预测值","Location","best");
hold off;原程序运行图窗结果:
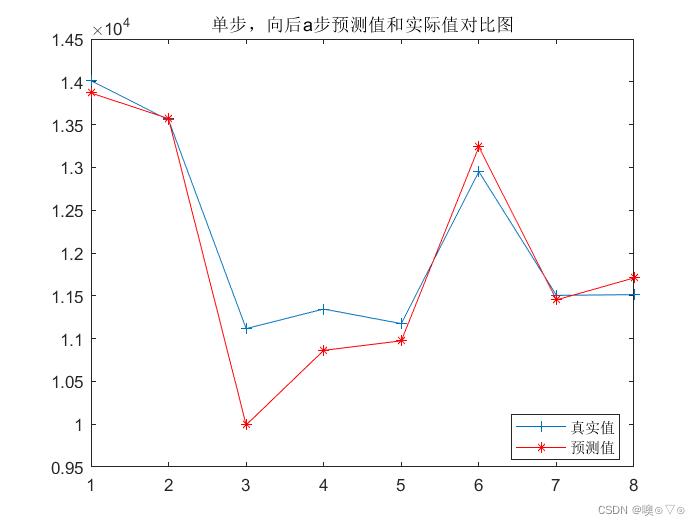
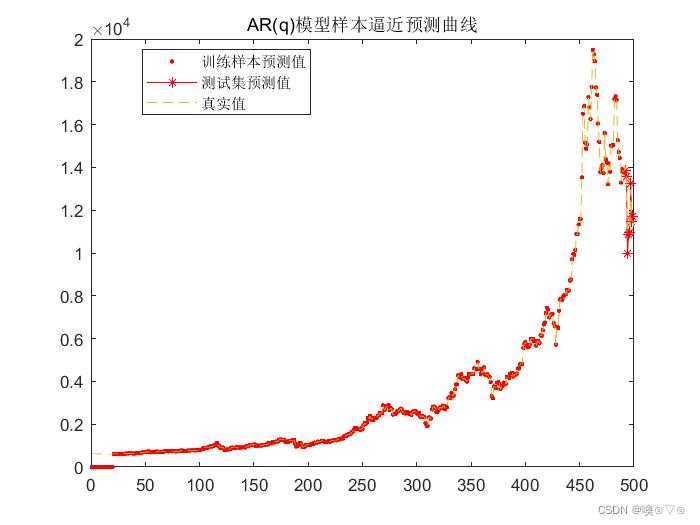
命令行输出结果:
MAPE6_a =
3.6147
MAPE6 =
12.5103
由上可知:单步预测准确率约为96.4%
多步(这里是8步)预测准确率约为87.5%
以上是关于ARIMA时间序列预测MATLAB代码模板(无需调试)的主要内容,如果未能解决你的问题,请参考以下文章