一个搜索问题包括一个状态空间，一个后续函数（包括动作，成本），一个开始状态和一个目标状态。

状态空间：当前“世界”所处的状态所有可能性的集合，假设整个状态空间是一段视频，那么状态就是视频的某一帧截图，它就是组成状态空间的一种可能。

后续函数：搜索问题的核心，它决定了代理下一步的动作是什么，也就是通过搜索算法来得出当前状态下如何决策是最符合预期的。后续函数中的参数必然含有动作和成本等协助判断的重要条件，通过这些条件就可以比对出当前状态下最好的决策。

解决方案：搜索问题的目标，是指将开始状态转换为目标状态的一系列操作（计划）。

计算状态空间的大小

将所有可能的环境/动作全部相乘。

很好理解，总状态空间就是代理位置、食物数量、敌人位置、代理方向四个因素来决定，而代理位置有120种可能，每一颗食物有存在/不存在两个状态，所以是2^30种可能，敌人有两个，一共有12种位置，所以敌人位置就有12^2种可能，代理的朝向有四种，就是4种可能。所以总状态空间的大小就是将它们相乘即可。

状态空间图与决策树

搜索树中的每个节点都是状态空间图中的一个完整路径，两者都可以按需构建，还可以互相转化，例如根据状态空间图绘制决策树。

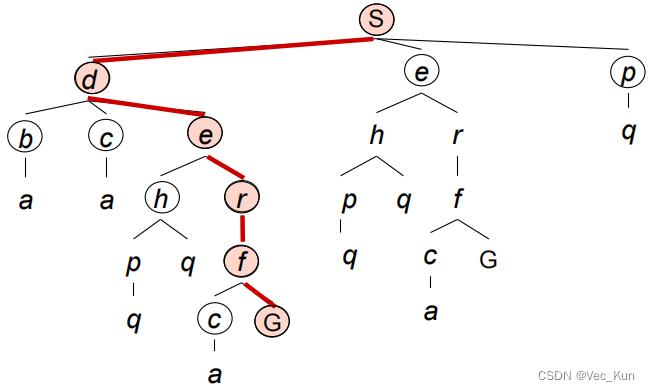
例：将图示状态空间图转化为决策树

我们引入两个列表：open_list 与 closed_list ，分别表示当前正在搜索的节点和已经搜索完毕的节点。open_list 初始只有起始状态S节点，而 closed_list 初始是空的。

求解过程：（这里其实使用了广度优先搜索）

	open_list	closed_list	备注
0	S	null	起始状态
1	d,e,p	S	分解起始节点S
2	b,c,e,p	S,d	依次分解S的子节点d，e，p
3	b,c,r,h,p	S,d,e	依次分解S的子节点d，e，p
4	b,c,r,h,q	S,d,e,p	依次分解S的子节点d，e，p
5	a,c,r,h,q	S,d,e,p,b	依次分解d的子节点b，c
6	a,r,h,q	S,d,e,p,b,c	依次分解d的子节点b，c
7	a,f,h,q	S,d,e,p,b,c,r	依次分解e的子节点r，h
8	a,f,q	S,d,e,p,b,c,r,h	依次分解e的子节点r，h(h的子节点p，q都已搜索过)
9	a,f	S,d,e,p,b,c,r,h,q	分解p的子节点q(q没有子节点)
10	f	S,d,e,p,b,c,r,h,q,a	依次分解剩余节点a，f(a没有子节点)
11	G	S,d,e,p,b,c,r,h,q,a,f	依次分解剩余节点a，f(f搜索到了目标节点G)
12	null	S,d,e,p,b,c,r,h,q,a,f,G	G进入了closed_list，搜索结束。

不知情搜索算法（Uninformed Search）

一些重要概念

完备：如果有解，一定能找到

最优：保证能找到代价最小的路径

时间复杂度：算法中的基本操作的执行次数，为算法的时间复杂度。

空间复杂度：空间复杂度算的是变量的个数

深度优先搜索（DFS）

从上到下，从左到右

边缘节点是后进先出的堆栈形式

在有限状态空间中，DFS是完备的

DFS不是最优的（它只能找到解，在一定条件下也并不保证代价最小）

广度优先搜索（BFS）

从左到右，从上到下

边缘节点是先进先出的队列形式

在有限状态空间中，BFS是完备的

在动作未加权时，BFS是最优的

补充：迭代深化（Iterative Deepening）是旨在将DFS和BFS的优势结合在一起，既然BFS能够找到最浅的(最优的)解，而DFS可能会先找到较深的解，因此我们可以限制深度，先限制DFS的深度为3去搜索，如果没有找到就用最大深度为4的DFS去找，以此类推......这样就可以找到最浅的解从而节约算力。

为什么？明明多次迭代，为何反而节约算力？这是因为大量的计算通常在更深层，我们在浅层多次迭代不会影响太多时间/空间复杂度。

代价敏感搜索（CCS）

如下图，如果使用上述方法，无论是DFS，BFS抑或是迭代深化，都只能得到经过节点最少的路径，但是如果每个动作标明代价（加权）的话，经过最少节点的路径就不一定是最优解了。因此，上述方法并不能在代价敏感搜索当中得到最优解，只能通过进一步计算，算出代价从而选出代价最小的路径来实现。

如上图，一共能找到两条路径：SderfG，SerfG。然而代价却分别是3+2+2+2+2=11和9+2+2+2=15，反而是经过节点较多的SderfG为最优解！

代价一致搜索（UCS）

优先扩展代价最小的节点

（类似Dijkstra算法）

它是完备的且最优的

但缺点是每个方向都可能扩展，且不知道目标的确切方向会显得盲目（不知情搜索/Uninformed Search是这样的）

【解决方法：将UCS和Greedy（贪心算法）结合起来形成A*算法...下文会讲到】

知情搜索算法（Informed Search）

如上图，知情搜索算法要讲解的分别为：启发式搜索，贪心搜索，A-star搜索，图搜索。

启发式搜索（Heuristics Search）

一个启发式是：

▪一个函数，估计一个状态与目标的距离

▪为一个特定的搜索问题设计

▪例子：曼哈顿距离，欧氏距离

如图，10+5就是曼哈顿距离：横坐标之差与纵坐标之差的和；11.2是欧氏距离：直线距离。

这样的函数就叫作启发式函数，记作h(x)。

贪心搜索（Greedy Search）

优先扩展当前状态下最优的节点

与UCS不同，UCS只考虑当前代价，而Greedy考虑了距离终点的距离。

它不是最佳的！通常它只考虑了距离而非代价，贪心算法的优劣很大程度上取决于启发式函数h(x)。

A*搜索

A*搜索综合了UCS和Greedy，有两个评估函数g(x)与h(x)，而A*搜索的决策取决于f(x)=g(x)+h(x)，综合考虑了前驱因素与后继因素。

A*是完备且最优的。当f(x)=g(x)+0时就找到了最优解。

【但这里有一个大前提】：那就是估计节点到终点的距离时（h(x)）一定要小于等于实际中s点到终点的距离才行，这叫做可采纳的试探（Admissible Heuristics）

例如下图：

因此，提出一个可接受的启发式方法是A*算法的需要解决的重要内容（实际上上文提到过的曼哈顿距离和欧氏距离就是很好的启发式方法）。

总结：

1. A*用前驱和（估计的）后继成本来决策；

2. A*在可接受的启发式方法下是最优的；

3. 启发式设计是关键所在，常用于宽松问题（Relaxed Problems）

图搜索（Graph Search）

一种在图中寻找路径的方法。 o 图中每个节点对应状态空间中的一个状态 ; o 每条连线对应一个操作符 ( 多数包含它的代价 ) 。

常用开关列表来解决问题： o 1) 建立一个只含有 起始节点 S 的 搜索图 G ，把 S 放到一个叫做 OPEN 的未扩展节点 表中 o 2) 建立一个叫做 CLOSED 的已扩展节点表， 其 初始为空表 o 3)LOOP ：若 OPEN 表是空表，则失败退出 o 4) 选择 OPEN 表上的第一个节点 , 把它从 OPEN 表移出并放进 CLOSED 表中。称此 节点为 节点 n o 5) 若 n 为 目标节点， 则有解并成功退出，此解是追踪图 G 中沿着指针从 n 到 S 这条路 径而得到的 ( 指针将在第 7 步中设置 ) o 6) 扩展节点 n ，同时 生成不是 n 的祖先的那些后继节点 的集合 M 。把 M 的这些成员 作为 n 的后继节点添入 图 G 中 o 7) 生成并记入 M 的子节点有以下三种情况： ① 未曾在G中出现过 的每个M成员：设置一个通向n的指针，并把它们加进OPEN表 ② 已经在OPEN表上 的每一个M成员，确定是否需更改通到n的指针方向。 ③ 已在CLOSED表上 的每一个M成员：除需确定该子节点指向父节点的指针外，还需确定其后继节 点指向 父节点 的指针(也就是，如该子节点的父节点根据需要(如代价值等)改变了，那就把该 子节点 移回Open表 ) o 8) 按某一任意方式或按某个探试值， 重排 OPEN 表 o 9)GO LOOP

例题

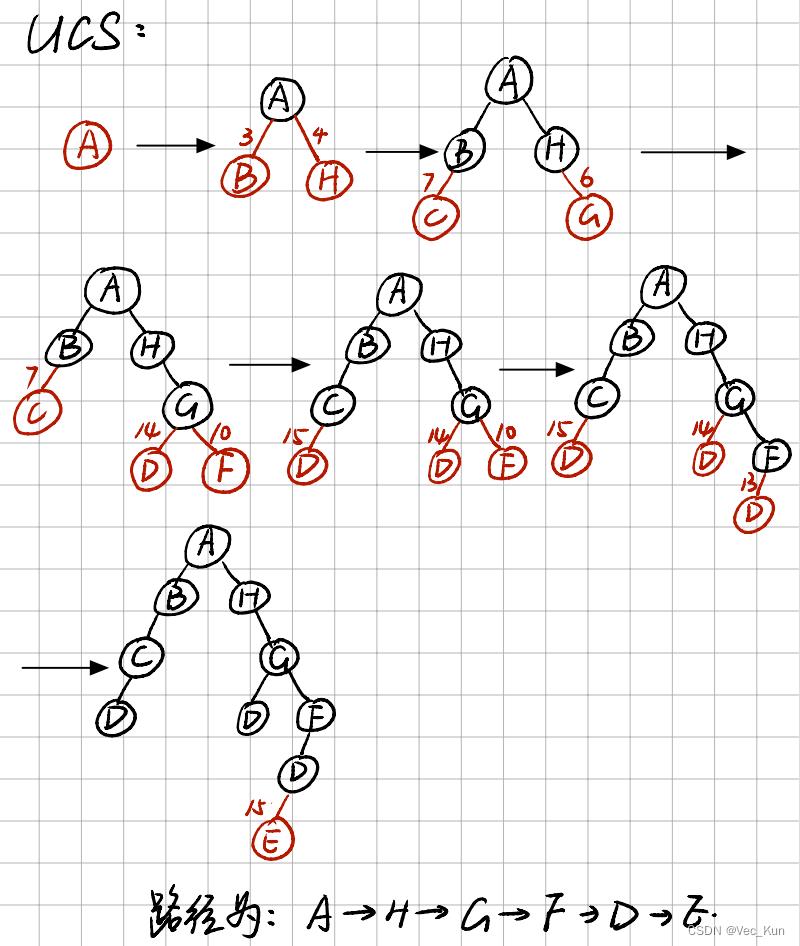
用要求的五种搜索算法计算从A到E的最优路径

解：

实验：A*算法解决八数码问题

八数码问题是在 3×3 的九宫格棋盘上，摆有 8 个刻有 1 ～ 8 数码的将牌。棋盘中有一个空格，允许紧邻空格的某一将牌可以移到空格中，这样通过平移将牌可以将某一将牌布局变换为另一布局。针对给定的一种初始布局或结构（目标状态），问如何移动将牌，实现从初始状态到目标状态的转变。如下图表示了一个具体的八数码问题求解。解：
选用已经走过的步数为g(n)，选择当前状态与目标状态相异的数字的曼哈顿距离之和为h(n)，得到估价函数f(n)=g(n)+h(n)。
选用open表与close表来维护状态图，如果当前状态已经在开/关列表中，取最小的一个保留。每次都选当前f(n)最小的作为待搜索节点。
判断无解情况：将当前状态与目标状态的九宫格转化为线性，分别计算逆序数的个数，如果逆序数奇偶性一致则有解，反之则无解。
具体代码后续会单独发一篇文章

对抗搜索

零和游戏（Zero-sum Games）

1. 代理有着相反的目标

2. 一个代理的分数高，另一个的分数就会必然变低

极小化极大算法（Minimax Algorithm）

Minimax算法又名极小化极大算法，是一种找出失败的最大可能性中的最小值的算法。Minimax算法常用于棋类等由两方较量的游戏和程序，这类程序由两个游戏者轮流，每次执行一个步骤。我们众所周知的五子棋、象棋等都属于这类程序，所以说Minimax算法是基于搜索的博弈算法的基础。该算法是一种零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，而另一方则选择令对手优势最小化的方法。

Minimax是一种悲观算法，即假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向，即对手具有完美决策能力。因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的，也就是让对方在完美决策下所对我造成的损失最小。

例子：

现在考虑这样一个游戏：有三个盘子A、B和C，每个盘子分别放有三张纸币。A放的是1、20、50；B放的是5、10、100；C放的是1、5、20。单位均为“元”。有甲、乙两人，两人均对三个盘子和上面放置的纸币有可以任意查看。游戏分三步：

甲从三个盘子中选取一个。
乙从甲选取的盘子中拿出两张纸币交给甲。
甲从乙所给的两张纸币中选取一张，拿走。

其中甲的目标是最后拿到的纸币面值尽量大，乙的目标是让甲最后拿到的纸币面值尽量小。

解：由于示例问题格局数非常少，我们可以给出完整的格局树。这种情况下我可以找到Minimax算法的全局最优解。而真实情况中，格局树非常庞大，即使是计算机也不可能给出完整的树，因此我们往往只搜索一定深度，这时只能找到局部最优解。

正方形表示甲决策（挑选最大），三角形表示乙决策（挑选最小）：

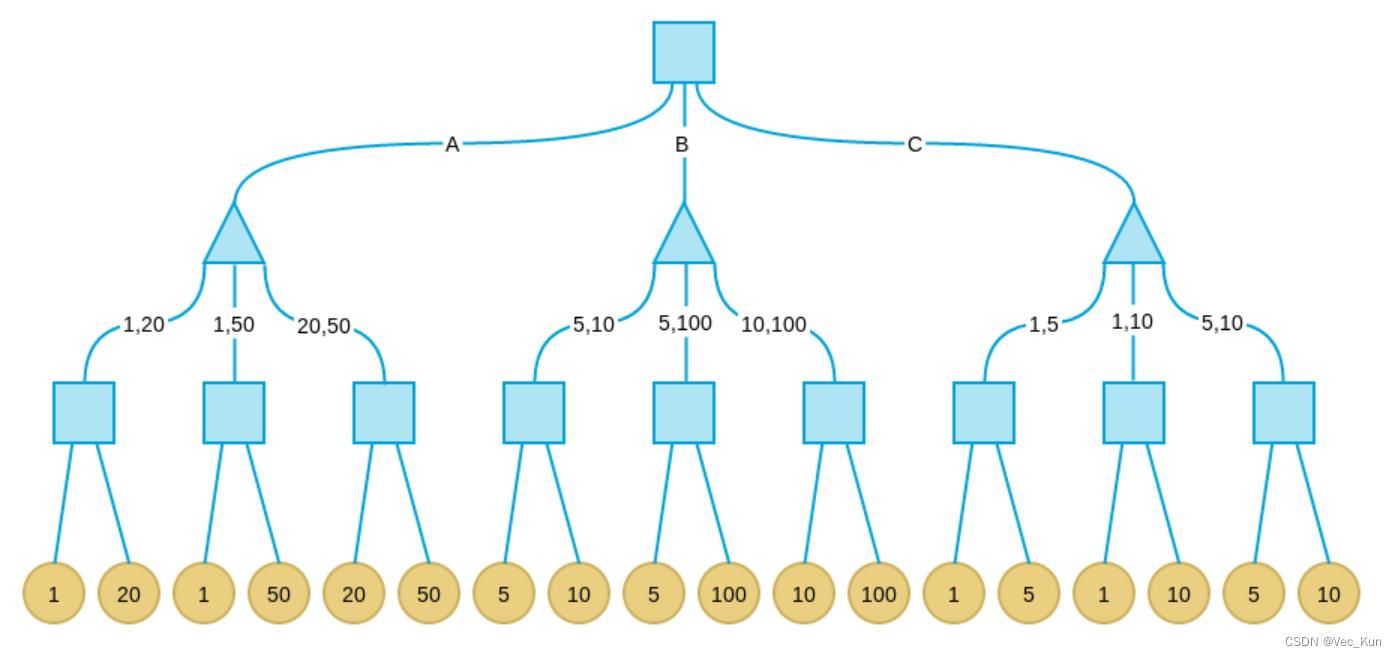
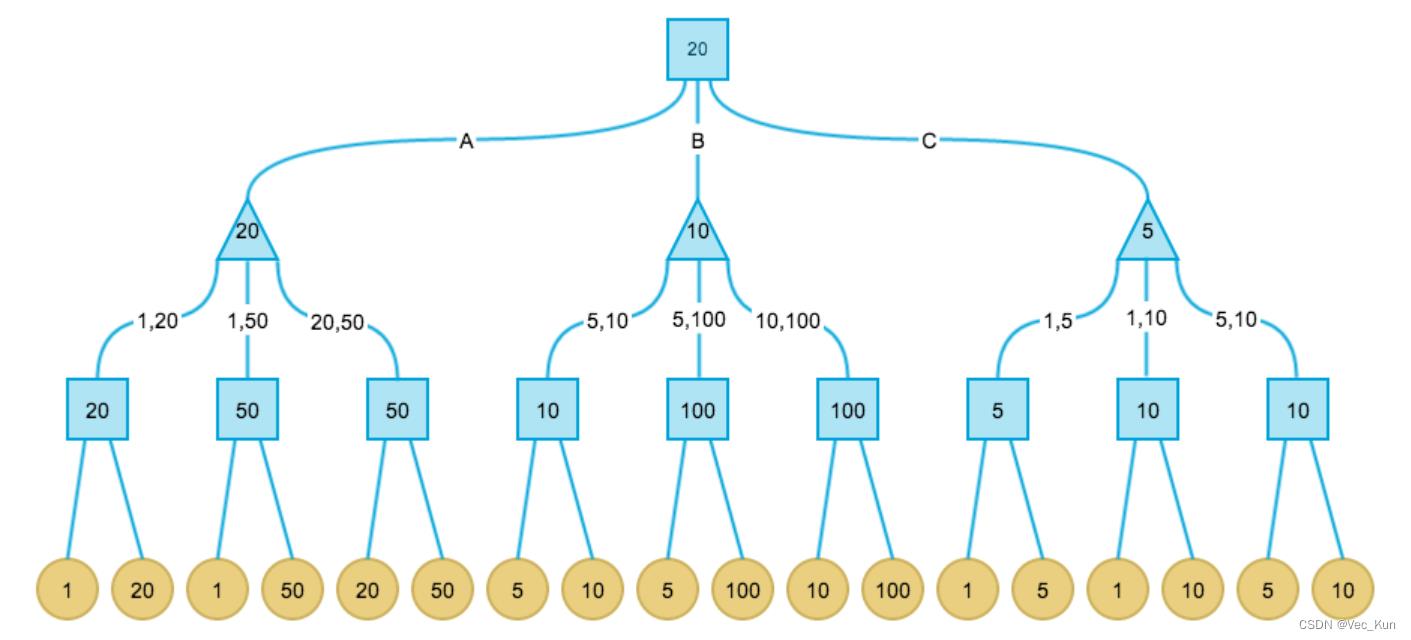最终甲期望得到的纸币面值为20，所以他应当选1号盘子为最优决策。

总结一下Minimax算法的步骤：

首先确定最大搜索深度D，D可能达到终局，也可能是一个中间格局。
在最大深度为D的格局树叶子节点上，使用预定义的价值评价函数对叶子节点价值进行评价。
自底向上为非叶子节点赋值。其中max节点取子节点最大值，min节点取子节点最小值。
每次轮到我方时（此时必处在格局树的某个max节点），选择价值等于此max节点价值的那个子节点路径。

注意：

真实问题一般无法构造出完整的格局树，所以需要确定一个最大深度D，每次最多从当前格局向下计算D层。
因为上述原因，Minimax一般是寻找一个局部最优解而不是全局最优解，搜索深度越大越可能找到更好的解，但计算耗时会呈指数级膨胀。
也是因为无法一次构造出完整的格局树，所以真实问题中Minimax一般是边对弈边计算局部格局树，而不是只计算一次，但已计算的中间结果可以缓存。

Alpha-Beta剪枝算法（Alpha-Beta Pruning）

剪枝算法规则：

1. Max层的α = max(α，它的所有子结点的评价值)，Max层的β = 它的父结点的β
2. Min层的β = min(β，它的所有子结点的评价值)，Min层的 α = 它的父结点的α
3. 当某个结点的 α >= β，停止搜索该节点的其他子结点
4. 叶结点没有 α 和 β

它极大减小了时间复杂度，在深层的搜索中减少了计算的负担。

我们一一说明这四条性质：
首先我们假设所有非叶结点的α初始化为负无穷，β初始化为正无穷。

若Max层中发现有一个子结点的评价值比当前所能达到的评价值更大，换句话说就是子结点的操作更优，那么将当前所能达到的评价值换成该子节点的评价值。并且由于它的父结点是从该Max层中选择最小的评价值，那么他就要判断一下当前的α是否大于它父结点的β。为了方便起见，我们将父结点的β赋给它自己的β，这样我们只需要比较它自己的α和β就可以了。
跟第一条类似，如果发现子结点中有比当前更优的操作（对对手更优，即对自己更差），那么就替换β，同时比较父结点最优解与当前解的大小，如果父结点已经有一个更优解，则不必继续搜索了。
Max层中，若某个结点的最优解已经大于它的父结点的最差解，则不必继续搜索，剪枝；Min层中，若某个结点的最差解已经小于它的父结点的最优解，则不必继续搜索，剪枝。
由于叶结点没有子结点，自然不需要计算 α 和 β。

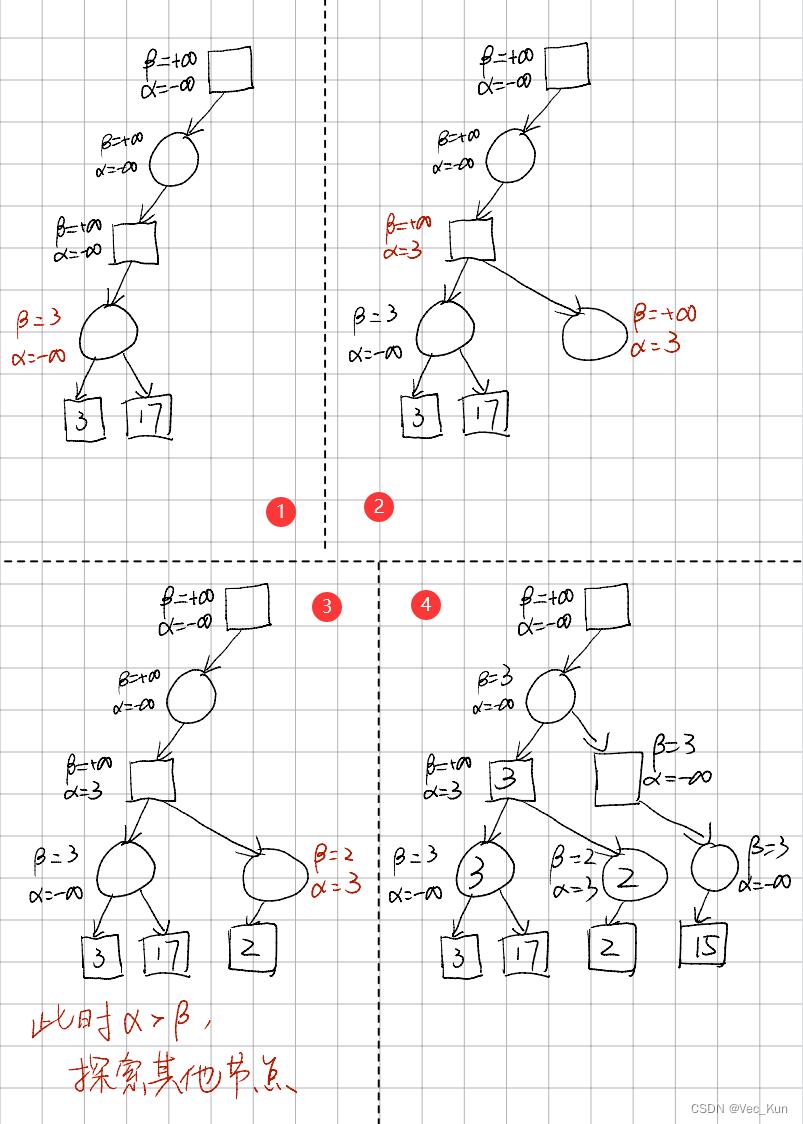
例题

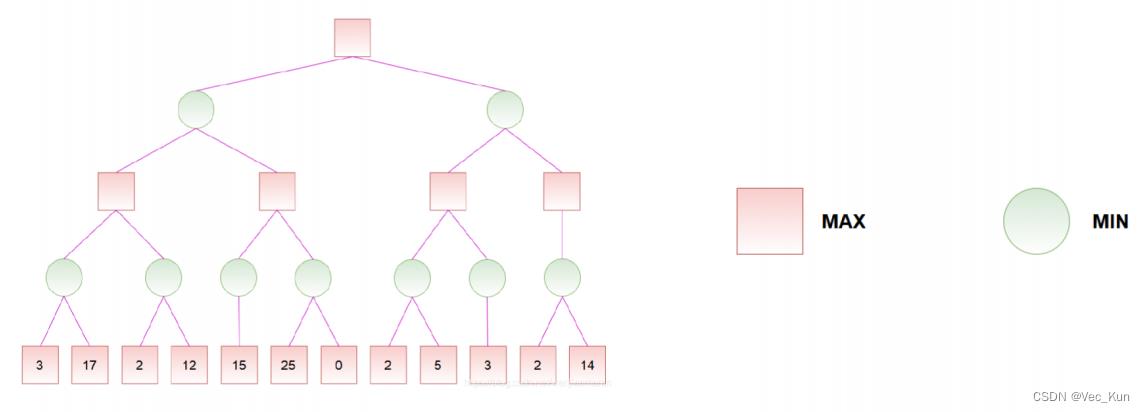
解：

总结

本篇主要讲解了搜索算法，包括不知情与知情搜索算法，不知情算法包括DFS、BFS、UCS等，知情搜索算法包括Greedy、A*、Graph等。还讲解了对抗搜索的相关概念与Alpha-Beta剪枝算法。

以上是关于电子科技大学人工智能期末复习笔记：搜索问题的主要内容，如果未能解决你的问题，请参考以下文章

电子科技大学人工智能期末复习笔记：一阶逻辑

电子科技大学人工智能期末复习笔记：概率与贝叶斯网络

人工智能导论期末复习合集

华南理工大学电力电子技术（王兆安）期末复习笔记2 第三章第四章