不要二(暴力+找规律)

Posted 2023-02-14 Aline2021-yxz

题目描述： 二货小易有一个W*H的网格盒子，网格的行编号为0 ~H-1，网格的列编号为0 ~W-1。每个格子至多可以放一块蛋糕，任意两块蛋糕的欧几里得距离不能等于2。 对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为: ( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根
小易想知道最多可以放多少块蛋糕在网格盒子里。

输入描述: 每组数组包含网格长宽W,H，用空格分割.(1 ≤ W、H ≤ 1000)

输出描述: 输出一个最多可以放的蛋糕数 

示例
输入 3 2 
输出 4

原题链接：不要二

题目分析：本质就是在一个W*H的二维数组中放入蛋糕，且蛋糕之间的欧几里得距离不能为2，问最多能放多少个蛋糕。

解法一：暴力解

我们首先将目光看向欧几里得距离表达式，看看能不能化简，
(x1-x2) * (x1-x2) + (y1-y2) * (y1-y2)的算数平方根为2，也就是说它等于4，那么我们将所有的可能都排列出来就是：

0+4=4
4+0=4
1+3=4
3+1=4
2+2=4

因为每个加数都是两个相同的数相乘算出来的，并且坐标之间的差都是整数，所以只有0+4和4+0是成立的。

0+4意味着x相减为0，也就是x坐标相等，y坐标相差2，同理4+0意味着x相差2，y相等。

简化了欧几里得距离，我们就可以暴力遍历数组来计算可以放的蛋糕数了，为了便于计数，我们不妨将数组全部初始化为1，不能放蛋糕的地方赋值为0。

int main()

	vector<vector<int>> board;
	int W, H;
	int count = 0;
	cin >> W >> H;
	board.resize(W);
	for (auto & x : board)
	
		x.resize(H,1);
	

	for (int i = 0; i < H; i++)//i控制行
	
		for (int j = 0; j < W; j++)//j控制列
		
			if (board[j][i] == 1)//可以放蛋糕
			
				count++;
				//越界判断
				if (i + 2 < H)
					board[j][i+2] = 0;
				if (j + 2 < W)
					board[j+2][i] = 0;
			
		
	

	cout << count << endl;
	return 0;

注意在遍历过程中对越界的判断。
这种方法确实比较简单，但是时间复杂度是比较高的，如果W和H都很大，那就比较耗费时间。

解法二：找规律

没错，这个题是有一定的规律的，只要找到规律，我们就可以弥补解法一的不足，不管你给多大的数组，我都能在一瞬间算出来！

首先，我们可以根据解法一画出下图：

这是9*6的数组能放蛋糕的图，黄色表示放蛋糕，红色表示不能放蛋糕，我们能根据这张图找到如下规律：

1. 如果行和列任何一个满足%4==0，那么能放蛋糕的位置就有WH/2个
   
   这个规律是显而易见的，因为44的数组中红方块和黄方块刚好一半一半，所以对于按倍数增长的数组也满足要求。

2. 如果行和列都满足%2==0，那么能放蛋糕的位置就有W*H/2+2个

不难看出只要行和列都为2的倍数，黄方块就比红方块多4个，如果将四个黄方块及四个红方块看为整体，算出来黄方块个数就是：
(W * H/4+1)/2*4=W * H/2+2;

3.其他情况

也就是行或列是或全是奇数的情况，这种情况我们选择“补偶法”，如果行为奇数，就补一个对称的图像，将行补为偶数，同理如果列为奇数，就将列补为偶数，如果都位奇数，那就补四个图形补为偶数

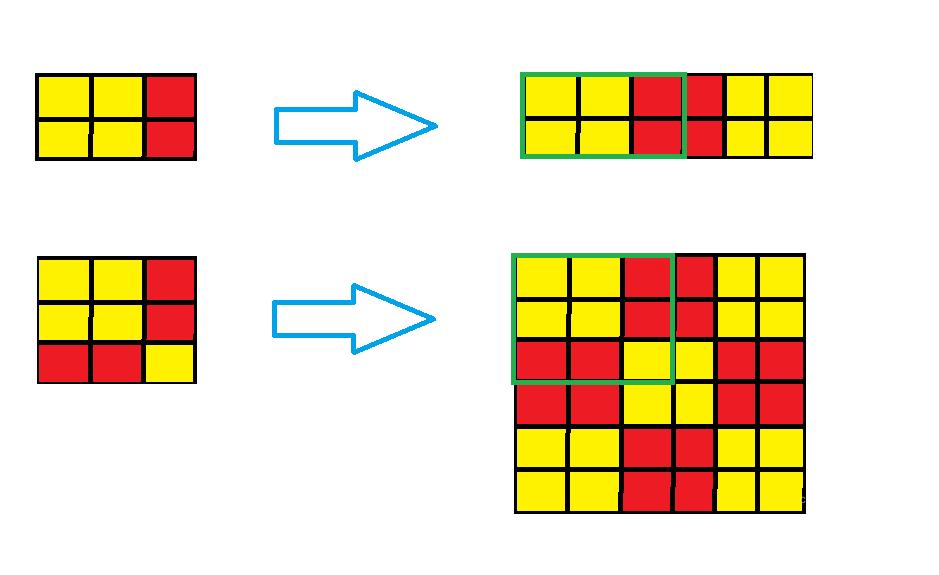
补为偶数后，我们就可以用第二种情况的方法算，但别忘了去掉补的那部分的个数：
行和列中一个为奇数另一个为2的倍数：(W * 2 * H/4+1) /2 * 4/2=W * H/2+1
行和列都为奇数：(W * 2 * H * 2 /4+1)/2 *4/4=W * H/2 +1/2,因为计算机算1/2为0，而前面W *H/2 必然会有0.5，所以该式仍可化简为 W *H/2+1；

上面就是这道题的几种情况，代码如下：

int main()

	int W, H;
	cin >> W >> H;
	int count = 0;
	if (W % 4 == 0 || H % 4 == 0)
		count = W*H / 2;
	else if (W % 2 == 0 && H % 2 == 0)
		count = W*H / 2 + 2;
	else
		count = W*H / 2 + 1;
	cout << count << endl;


	return 0;

补偶法是其他博主的博客对我的启发，并非抄袭！