Matlab数学建模模糊综合评价
Posted 九死九歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Matlab数学建模模糊综合评价相关的知识,希望对你有一定的参考价值。
二、模糊集
1.模糊集的概念
对于一些指标,只有属于和不属于。例如数学命题,只要属于真命题he不属于真命题两种状态。这种情况下,我们可以用集合表示。比如某集合包含所有真命题,某集合包含所有整数。
但对于有些指标,则是模糊的。比如帅和丑、好和坏、高和低。他们不具有“非此即彼”的排中律,而具有“亦此亦彼”的模糊性。
为了研究这种模糊关系,我们引入模糊集的概念。
给定域论 U U U,对于某个模糊集 A A A和任意 x ∈ U x\\in U x∈U,都能确定一个整数 μ A ( x ) ∈ [ 0 , 1 ] \\mu_A(x)\\in [0, 1] μA(x)∈[0,1]用来表示 x x x属于 A A A的程度。映射:
x ∈ U → μ A ( x ) ∈ [ 0 , 1 ] x\\in U\\rightarrow\\mu_A(x)\\in[0,1] x∈U→μA(x)∈[0,1]
称 A A A为隶属函数,函数 μ A ( x ) \\mu_A(x) μA(x)为 x x x对 A A A的隶属度。
例如集合 U U U为全体人类,集合 A A A代表全体好人,这是一个模糊的概念。若 μ A ( 我 ) = 0.75 \\mu_A(我) = 0.75 μA(我)=0.75,就说明全世界有 75 % 75\\% 75%的人认为我是好人。
2.模糊集的运算
( 1 ) 包 含 : A ⊂ B ⟺ μ A ( x ) ≤ μ B ( x ) (1)包含:A\\subset B\\iff\\mu_A(x)\\leq\\mu_B(x) (1)包含:A⊂B⟺μA(x)≤μB(x) ( 2 ) 相 等 : A = B ⟺ μ A ( x ) = μ B ( x ) (2)相等:A = B\\iff\\mu_A(x) = \\mu_B(x) (2)相等:A=B⟺μA(x)=μB(x) ( 3 ) 相 交 : C = A ∩ B ⟺ μ C ( x ) = μ A ( x ) ∧ μ B ( x ) (3)相交:C=A\\cap B\\iff\\mu_C(x)=\\mu_A(x)\\land\\mu_B(x) (3)相交:C=A∩B⟺μC(x)=μA(x)∧μB(x) ( 4 ) 相 并 : C = A ∪ B ⟺ μ C ( x ) = μ A ( x ) ∨ μ B ( x ) (4)相并:C=A\\cup B\\iff\\mu_C(x)=\\mu_A(x)\\lor\\mu_B(x) (4)相并:C=A∪B⟺μC(x)=μA(x)∨μB(x) ( 5 ) 补 集 : A C ⟺ μ A C ( x ) = 1 − μ A ( x ) (5)补集:A^C\\iff \\mu_A^C(x)=1-\\mu_A(x) (5)补集:AC⟺μAC(x)=1−μA(x) ( 6 ) 内 积 : A ⊙ B ⟺ ∨ x ∈ U ( μ A ( x ) ∧ μ B ( x ) ) (6)内积:A\\odot B\\iff\\lor_x\\in U(\\mu_A(x)\\land\\mu_B(x)) (6)内积:A⊙B⟺∨x∈U(μA(x)∧μB(x)) ( 7 ) 外 积 : A ⊗ B ⟺ ∧ x ∈ U ( μ A ( x ) ∨ μ B ( x ) ) (7)外积:A\\otimes B\\iff\\land_x\\in U(\\mu_A(x)\\lor\\mu_B(x)) (7)外积:A⊗B⟺∧x∈U(μA(x)∨μB(x))
其中 ∧ \\land ∧和 ∨ \\lor ∨分别代表取最小和取最大运算。
3.隶属函数的确定
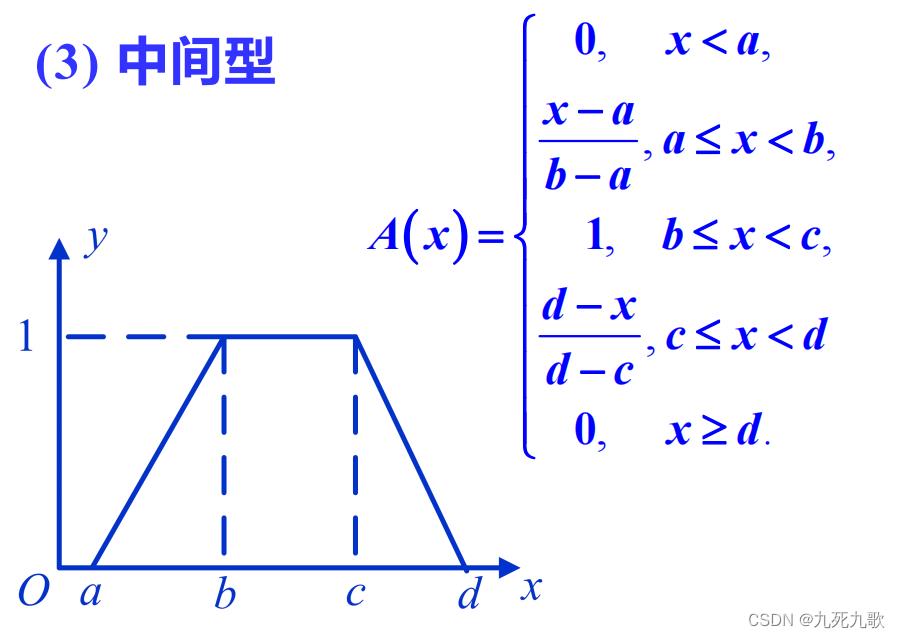
确定隶属函数常用的是模糊分布法,下面简要介绍模糊分布法的常用梯形分布。


二、模糊综合评价
1.确定评价指标和评价等级
设 U = u 1 , u 2 , ⋯ , u m U=\\u_1, u_2, \\cdots, u_m\\ U=u1,u2,⋯,um是被评价对象的m个因素,即评价指标。而 V = v 1 , v 2 , ⋯ , v m V=\\v_1, v_2, \\cdots, v_m\\ V=v1,v2,⋯,vm为每一因素所处的n种评语,即评价等级。评价等级一般只划分3~5个。
例如评价采用模糊评价了解原批们对八重神子的喜欢程度。 U = 强 度 , 人 气 , x p , 人 设 , V = 很 喜 欢 , 喜 欢 , 一 般 , 不 喜 欢 U=\\强度,人气,xp,人设\\,V=\\很喜欢, 喜欢, 一般, 不喜欢\\ U=强度,人气,xp,人设,V=很喜欢,喜欢,一般,不喜欢
2.构造模糊综合评价矩阵
设 r i j r_ij rij代表指标 u i u_i ui对等级 v j v_j vj的隶属度,通常要将 r i j r_ij rij归一化处理。
则可以构建矩阵:
R = ( r i j ) m × n = ( r 11 r 12 ⋯ r 1 n r 21 r 22 ⋯ r 2 n ⋮ ⋮ ⋱ ⋮ r m 1 r m 2 ⋯ r m n ) R=(r_ij)_m\\times n= \\beginpmatrix r_11 & r_12 & \\cdots & r_1n\\\\ r_21 & r_22 & \\cdots & r_2n\\\\ \\vdots & \\vdots & \\ddots & \\vdots\\\\ r_m1 & r_m2 & \\cdots & r_mn\\\\ \\endpmatrix R=(r