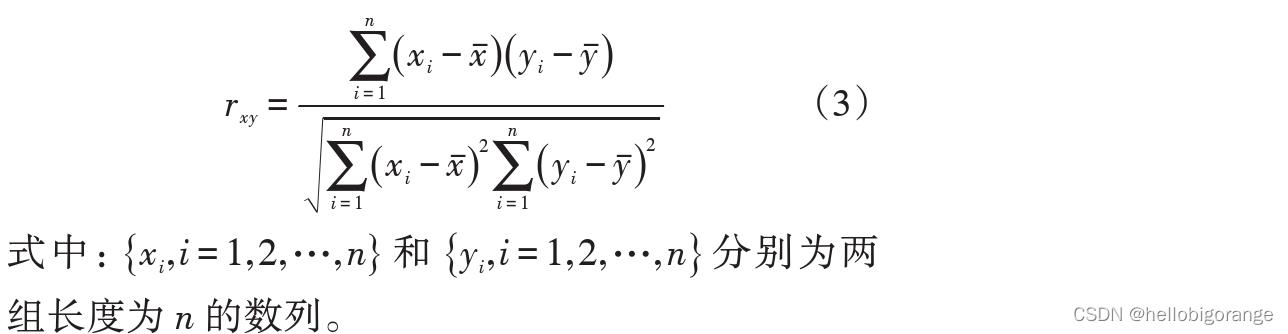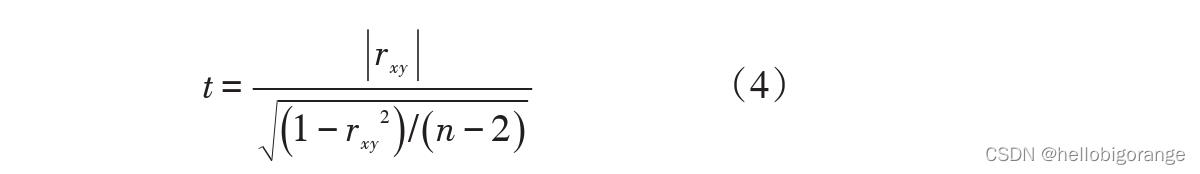时间序列—显著相关性和滞后性分析_python

Posted 2023-02-03 hellobigorange

😊作者简介：大家好我是hellobigorange,大家可以叫我大橙子
💖本文摘要：本文讲述了两个时间序列(信号)的相关性分析，可以利用相关性分析进行特征筛选。此外本文还讲了怎么判断时间序列的滞后性的方法。

文章目录

• 一、分析数据的相关性和滞后性的必要性
• • 1.1 相关性
  • 1.2 滞后性
• 二、相关性分析
• • 2.1 皮尔逊相关系数
  • 2.2 负荷相关性分析_python实现
  • 2.2 灰色关联度分析
  • 2.3 其他方法
  • 2.4 特征相关性、显著性分析热力图可视化
• 三、滞后性
• • 3.1 TLCC
  • 3.2 互相关性
• 参考链接

一、分析数据的相关性和滞后性的必要性

1.1 相关性

在使用机器学习模型对数据进行训练的时候，需要考虑数据量和数据维度，在很多情况下并不是需要大量的数据和大量的数据维度，这样会造成机器学习模型运行慢，且消耗硬件设备。除此之外，在数据维度较大的情况下，还存在”维度灾难“的问题。
在开展特征工程时，数据的降维方法思想上有两种

• 特征降维： 一种是例如主成分分析方法(PCA)破坏数据原有的结构从而提取数据的主要特征
• 特征选取： 按照一定的法则来对数据的属性进行取舍达到降维的目的。
  • 相关性分析：分析特征和因变量（标签列）的相关性，保留相关性强的。
  • 方差：对于方差太小的，说明特征的整体变化不大，可以剔除。

1.2 滞后性

有时候将某个特征滞后一定时间后， 得到一个新的特征， 可能会与目标变量有更强的相关性，个人理解，一般某个特征变量, 你有足够的专业知识或推断认为其可能存在滞后性后， 再考虑这个问题就可以。

比如我最近做的管道的入口压力和出口压力，二者都是由传感器同时采集的，但是由于管道是有一定长度的，因此出口压力有可能会比入口压力传导上有一定的延迟。 再比如产量对负荷的影响中，产量数据并不是实时统计的，可能也会存在特征统计的滞后性问题。

二、相关性分析

欧式距离：在时间序列预测有缺陷，不能辨认形状的相似度，适用于距离度量.

2.1 皮尔逊相关系数

在统计学中，皮尔逊相关系数（pearson correlation coefficient）用于度量两个变量X和Y之间的线性相关性，其值介于-1与1之间。在自然科学领域中，该系数广泛用于度量两个变量之间的线性相关程度。

1、本文采用Pearson相关系数来考察各类因素x_i对因变量y的影响力，相关系数按公式（3）计算

2、两变量之间的相关性可由相关系数初步决定，但须进行显著性检验再最后判断。其显著性检验公式为

3、评判标准:
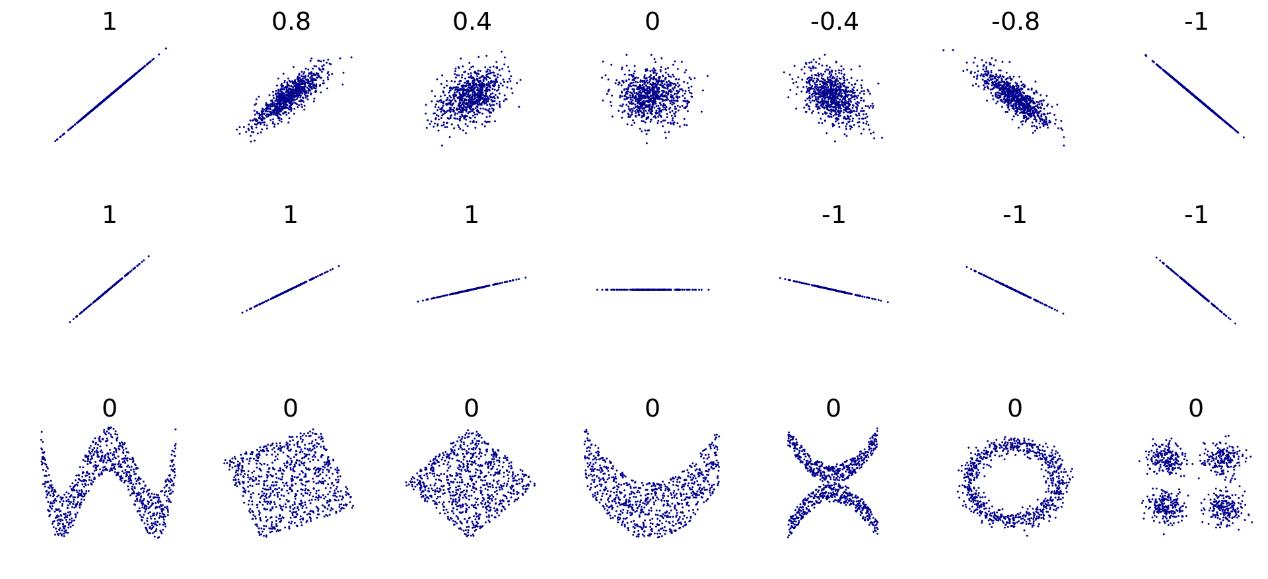
若r＞0，表明2个变量是正相关，即一个变量的值越大，另一个变量的值也会越大；若 r＜0，表明 2个变量是负相关，即一个变量的值越大，另一个变量的值反而会越小。r 的绝对值越大表明相关性越强。

直观感受不同的Pearson相关系数对应的图像

2.2 负荷相关性分析_python实现

"data.csv"
 最大负荷,常住人口,人均收入,GDP,农业总值,工业总值,第三产业产值,年平均温度,年降水,年售电量
 21.2,6.8,3752,2.21,2.4,11.5,21,15.9,998.5,0.9
 22.7,7,3897,2.78,2.43,11.8,22,15.6,995.2,0.98
 24.36,7.15,4058,3.05,2.67,12.14,22.7,16.4,1002.6,1.1
 26.22,7.28,4237,3.82,1.85,12.2,23,17.1,1237,1.23
 28.18,7.42,4552,4.34,2.36,13,24.4,16.1,1170,1.36
 30.16,7.55,4998,5.86,2.88,13.6,25.4,16.6,1001.3,1.49
 86.6,10.23,22760,84.94,31,72,73,16.2,1232.5,5.41

"""
DataFrame.corr(method='pearson', min_periods=1)

参数说明：
method：可选值为‘pearson’, ‘kendall’, ‘spearman’
pearson：Pearson相关系数来衡量两个数据集合是否在一条线上面，即针对线性数据的相关系数计算，针对非线性数据便会有误差。
kendall：用于反映分类变量相关性的指标，即针对无序序列的相关系数，非正态分布的数据
spearman：非线性的，非正态分布的数据的相关系数
min_periods：样本最少的数据量
返回值：各类型之间的相关系数DataFrame表格。"""
data = pd.read_csv("data.csv")
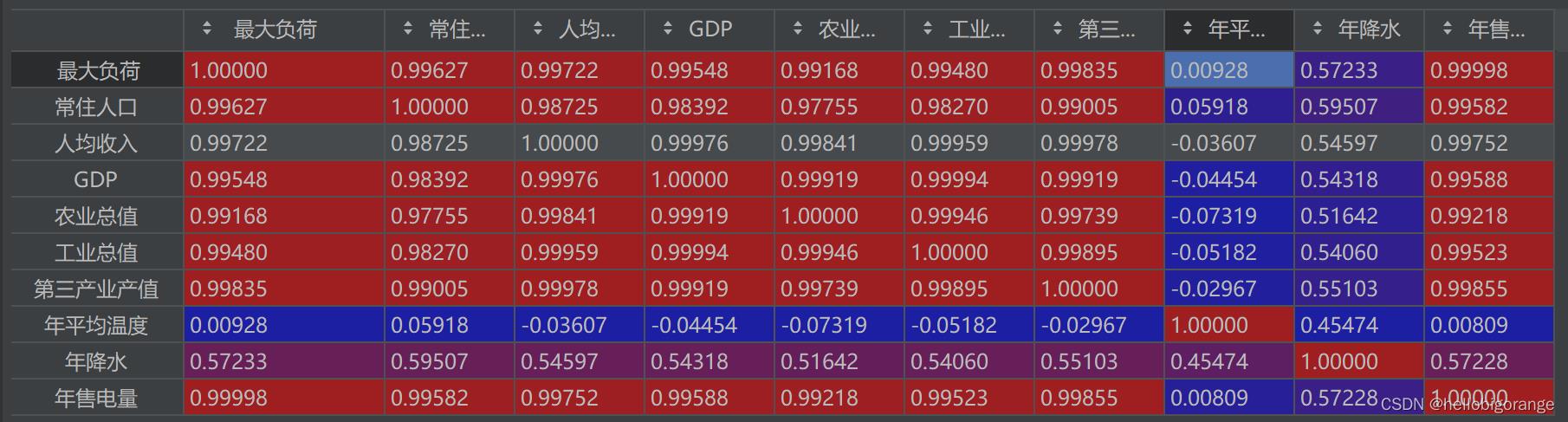
data.corr()

结果分析：
下图显示就是各个特征之间的相似性分析，第一列就是各特征与因变量的关系，里面显示年平均降水量和年降水相关性偏低。对比之前的灰色关联度分析的结果差异过大，经思考应该是灰色关联度无量纲处理的问题，采用MinMaxScaler或者StandardScaler后，二者结果相近.

2.2 灰色关联度分析

灰色关联分析适用于探究非线性相关性。灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度。

我之前写的一篇GRA文章：灰色关联度分析法(GRA)_python

2.3 其他方法

时间序列相似性度量综述

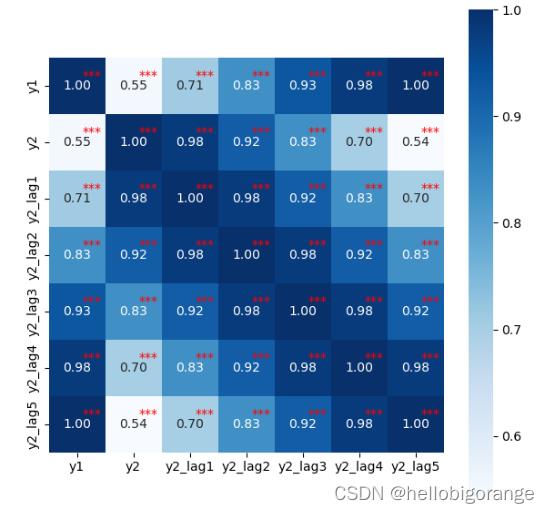
2.4 特征相关性、显著性分析热力图可视化

1、如果呈现出显著性（结果右上角有*号，此时说明有关系；反之则没有关系）；有了关系之后，关系的紧密程度直接看相关系数大小即可。一般0.7以上说明关系非常紧密；0.4_{0.7之间说明关系紧密；0.2}0.4说明关系一般。

2、如果说相关系数值小于0.2，但是依然呈现出显著性（右上角有*号，1个*号叫0.05水平显著，2个*号叫0.01水平显著；显著是指相关系数的出现具有统计学意义普遍存在的，而不是偶然出现），说明关系较弱，但依然是有相关关系。

# -*- coding: utf-8 -*- 
# @Time : 2023/1/16 14:40 
# @Author : Orange
# @File : test.py.py
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import pearsonr
import numpy as np


def feature_corr(df):
    corr = round(df.corr(), 2)
    # ax1 = plt.gca()
    fig_legth = len(df.columns)
    plt.subplots(figsize=(fig_legth, fig_legth), nrows=1)
    sns.heatmap(corr, annot=True, vmax=1, square=True, cmap="Blues", fmt='.2f')

    rlist = []
    plist = []
    # 计算显著性水平并绘制
    for i in df.columns:
        for j in df.columns:
            r, p = pearsonr(df[i], df[j])
            rlist.append(r)
            plist.append(p)

    rarr = np.asarray(rlist).reshape(fig_legth, fig_legth)
    parr = np.asarray(plist).reshape(fig_legth, fig_legth)
    for m in np.arange(0.6, fig_legth+0.6, 1):
        for n in np.arange(0.4, fig_legth+0.4, 1):
            pv = (parr[int(m), int(n)])
            rv = (rarr[int(m), int(n)])
            if abs(rv) > 0.5:
                if pv < 0.05 and pv >= 0.01:
                    plt.text(m, n, "*", size=10, color="r")
                elif pv < 0.01 and pv >= 0.001:
                    plt.text(m, n, "**", size=10, color="r")
                elif pv < 0.001:
                    plt.text(m, n, "***", size=10, color="r")
            else:
                if pv < 0.05 and pv >= 0.01:
                    plt.text(m, n, "*", size=10, color="black")
                elif pv < 0.01 and pv >= 0.001:
                    plt.text(m, n, "**", size=10, color="black")
                elif pv < 0.001:
                    plt.text(m, n, "***", size=10, color="black")

    plt.savefig('特征相关性显著性热力图.png')  # 保存图⽚完整
    plt.show()

    return corr


if __name__ == '__main__':
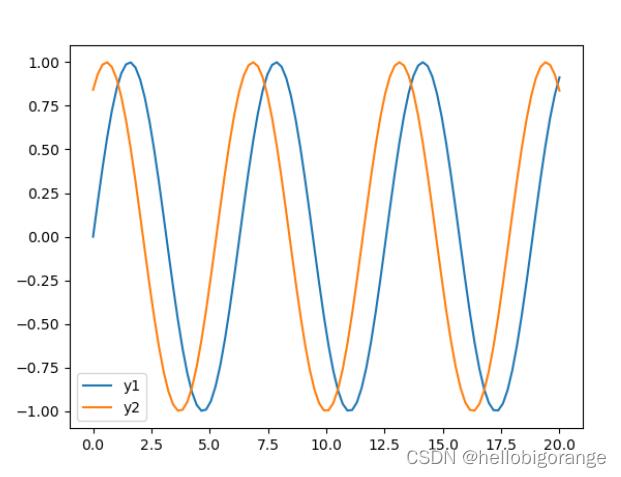
    x = np.linspace(0, 20, 100)
    y1 = np.sin(x)
    y2 = np.sin(x + 1)
    df = pd.DataFrame(np.array([y1, y2]).T, columns=['y1', 'y2'])

    for i in range(1,6):
        df["y2_lag" + str(i)] = df['y2'].shift(i)

    df.dropna(inplace=True)
    feature_corr(df)

可以看出y1与y2_lag5显著性相关

三、滞后性

3.1 TLCC

TLCC算法: 将其中一个时间序列y2滞后-k——k阶，与另一个时间序列y1一起计算pearson系数。假设在i阶的相关性最强，说明y2滞后y1有i阶；若i<0，则y2超前y1有i阶。

3.2 互相关性

互相关性 np.correlate: 主要原理就是将时间序列y2滞后-k——k阶，与时间序列y1计算点积和(主要看一个方向性，若相关性最强时，序列的正负方向一致，此时点积应该是最大的)，若第i阶的点积和最大，则说明y2滞后y1有i阶，若i<0，则y2超前y1有i阶。


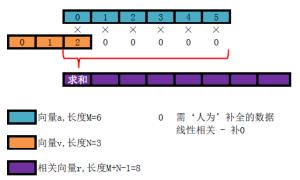
方法二详细原理参考: 互相关（cross-correlation）及其在Python中的实现
代码

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

"""原始数据"""
x = np.linspace(0, 20, 100)
y1 = np.sin(x)
y2 = np.sin(x + 1)
plt.plot(x, y1)
plt.plot(x, y2)
plt.legend(['y1', 'y2'])
plt.show()

"""利用pearson计算滞后性"""
# 从图中可以看出y2滞后5阶
data_cor = pd.DataFrame(np.array([y1, y2]).T, columns=['y1', 'y2'])
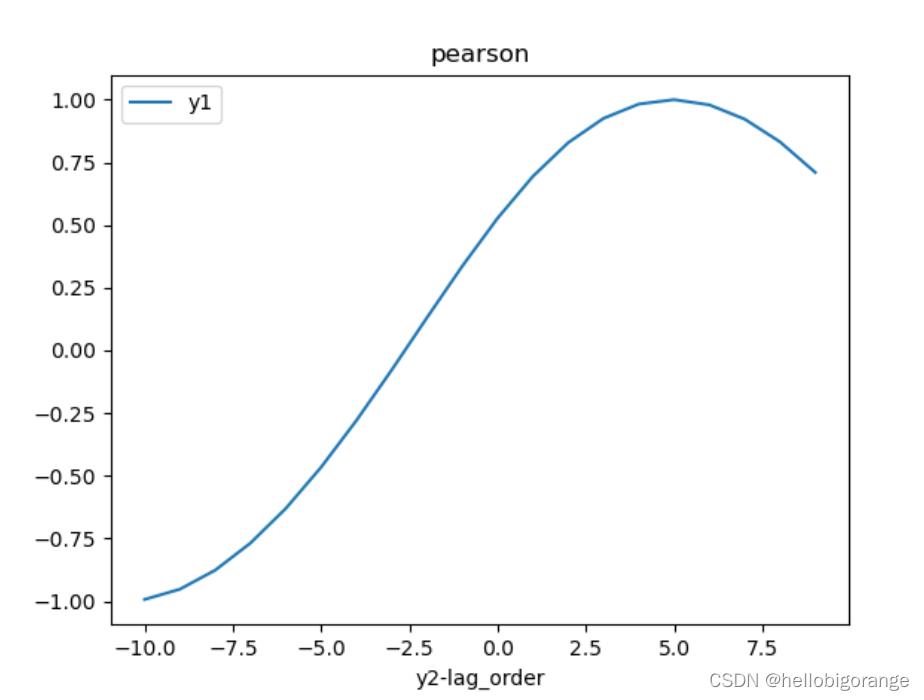
for i in range(-10, 10):
    data_cor[str(i)] = data_cor['y2'].shift(i) 
data_cor.dropna(inplace=True)
p = data_cor.corr()
print("person相关系数：\\n", data_cor.corr())
plt.plot(range(-10, 10),data_cor.corr().iloc[0][2:].values)
plt.legend(['y1', 'y2'])
plt.title('pearson')
plt.xlabel('y2-lag_order')
plt.show()

"""利用互相关性计算滞后性"""
a = np.correlate(y1, y2, mode="same")
print("y1滞后y2：", len(a) // 2 - a.argmax())  # 若为负数，说明y1超前y2
# plt.plot(x[:-5],y1[5:]) # 结论y1超前y2五个单位。将y1时间向前错位即可重合

结果分析:
原始序列:

pearson,可以看出y2滞后y1有5阶的时候, pearson相关性最强. 通样滞后5阶时自相关点积和最大.

参考链接

【1】机器学习相关性的度量
【2】皮尔逊(Pearson),二维相关性分析(TDC),灰色关联分析,最大信息系数(MIC)
【3】互相关（cross-correlation）及其在Python中的实现
【4】利用时序相关性分析和聚类提升销量预测模型
【5】如何确定两个时间序列是否存在相关性
【6】时间序列联动分析
【7】有哪些有效的可以衡量两段或多段时间序列相似度的方法？
【8】机器学习_各种距离度量总结