关于排序中最少交换次数的证明(置换环)

Posted 2023-01-24 Harris-H

关于排序中最少交换次数的证明(置换环)

利用置换环可以进行证明。这里我只做感性的证明。

问题

对于长度为$n$的数组$a$，$a_i\in N$，$a_i$互不相同，每次操作可以选择任意两个位置$i,j$交换$a_i,a_j$，要求排序的最少交换次数。

答案

最少交换次数$cn{t}_{swap}=n-cn{t}_{circle}$

$cn{t}_{circle}$ 就是数组中置换环的个数。

方法

首先我们对数组进行排序，然后进行映射到$[1,n]$这个区间。

比如$m(a_j)=i$， 说明$a_j$这个元素最终的位置应该在$i$。可以理解为$j$向$i$连一条有向边。

同时再开一个数组标记位置是否访问过。我们利用$m$数组暴力找环的个数即可。

时间复杂度：$O(n)$

int getSwapCnt(vector<int>&a)
	int n = a.size(),cnt=0;
	vector<int>b(a);
	sort(b.begin(),b.end());
	unordered_map<int,int>m;
	vector<bool>vis(n);
	for(int i=0;i<n;i++) m[b[i]] = i;
	for(int i=0;i<n;i++)
		if(!vis[i])
			int j = i;
			while(!vis[j])
				vis[j] = true;
				j = m[a[j]];
			
			cnt++;
		
	return cnt;

下面这个写法是反向的一个建边，可以允许$a_i$相同。

int a[N],b[N],n;
bool vis[N];
bool cmp(int &x,int &y)
	return a[x]<a[y];

int getSwapCnt()
	int cnt=0;
	for(int i=1;i<=n;i++) b[i] = i;
	sort(b+1,b+n+1,cmp);
	for(int i=1;i<=n;i++)
		if(!vis[i])
			int j = i;
			while(!vis[j])
				vis[j] = true;
				j = b[j];
			
			cnt++;
		
	return cnt;

---

简要证明

显然如果有$n$个环的话，说明此时已经排序好了。$cnt=n-n=0$。

那么我们的目标就是要达到$n$个环。

每次我们可以选择一个环中的两个结点进行交换，这样环的个数会加1，变成两个。如下图所示：

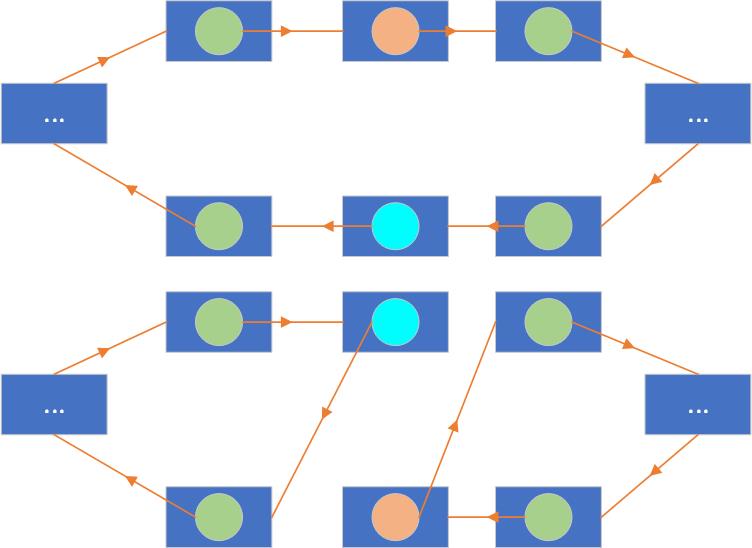
那么既然每次操作环个数加1，我们已经有$m$个环了，那么要达到$n$个环，显然最少次数是$n-m$次操作，加$n-m$个环。

所以答案就是$n-m$。