2020第6届中国大学生程序设计竞赛CCPC长春站， 签到题3题

Posted 2023-01-22 小哈里

文章目录

• • • A.Krypton
    • D.Meaningless Sequence
    • F.Strange Memory

补题链接：https://codeforces.com/gym/102832

A.Krypton

time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
In the future several years, you will surely remember that you once participated in a special China Collegiate Programming Contest. Due to COVID-19, all parties had paid a lot of effort to eventually hold a rare online programming contest. As a problem writer, I would also like to express my sincere gratitude to the organizing committee, all the contestants and others who have worked hard in this process. I also sincerely wish you good results in this special contest and a special and sweat memory in the future.

Maybe several years later, you may recall that …

Once there was a mobile game, where there was a virtual currency called coupon that could only be purchased by RMB. Kelo found that relying on his liver alone cannot make him stronger, so he decided to purchase some coupons. When he opened the recharge page, he found that this game had seven recharge columns, and was holding an activity called “First Recharge Reward”. If it was the first time a recharge column was chosen, some additional coupons would be given to the player as a reward. A player might receive several rewards if he chose several different recharge columns. A column could be chosen for arbitrary times, but there would be no additional reward except for the first time it was chosen. Here is a table describing the price, amount of coupons in normal case and additional first recharge rewards of each column.

Price (RMB yuan)162888198328648Normal amount (coupons)1060280880198032806480First recharge reward (coupons)8182858128198388
Kelo had recently earned n yuan by writing problems for China Collegiate Programming Contest. He decided to recharge all these n yuan to the game, and hoped to get as many coupons as possible with these hard-earned money.

Input
The only line contains an only integer n (1≤n≤2000).

Output
Print the maximum amount of coupons Kelo might get.

Examples
inputCopy
100
outputCopy
1084
inputCopy
198
outputCopy
2108

题意：

• 表格给出7种买东西的方式，第一次购买会有返利，之后购买没有返利。
• 现在有N元，问最多能买进多少个。

思路：

• 注意本题是不能贪心的。（6+28+88+198+328的情况要比648更优）
• 考虑混合背包，第一次有返利的跑01背包。之后没有返利，购买次数无限制，跑完全背包。
• 因为除了首充奖励之外，其余的RMB与点券比例都是1：10， 所以只需要考虑首充的情况。
  因为数据范围只有2^7，也可以暴力枚举是否首充。

#include<bits/stdc++.h>
using namespace std;
int c[7] = 1,6,28,88,198,328,648;
int f[7] = 8,18,28,58,128,198,388;
int main()
    int n;  cin>>n;
    int ans = 0;
    for(int i = 0; i < (1<<7); i++)
        int price = 0, reward = 0;
        for(int j = 0; j < 7; j++)
            if((i>>j)&1)
                price += c[j];
                reward += f[j];
            
        
        if(price <= n)ans = max(ans, reward);
    
    ans += n*10;
    cout<<ans<<"\\n";
    return 0;

D.Meaningless Sequence

D. Meaningless Sequence
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Once there was a mathematician, who was obsessed with meaningless number sequences. Here is one of them.

an=1,c⋅max0≤i<nan&i,n=0otherwise,
where & denotes the bitwise AND operation.

As a mathematician, he could easily tell what an was for any n, but he wanted to test you. You are required to tell him

(∑i=0nai)mod(109+7)
to convince him that you have a deep understanding of this (although meaningless) sequence.

Input
The only line contains two integers n and c (0≤n<23000,0≤c≤109).

Specially, n is given in binary presentation. c is given in decimal presentation normally.

Output
Print what you are expected to tell the mathematician normally in decimal presentation.

Example
inputCopy
1000 3
outputCopy
67

题意：

• 给出n和c，以及an的定义，求a0+a1+a2+…+an的值。

思路：

• 给n和c打个表，不难发现，an定义等价于$a_i=c^{popcount(i)}$，其中popcount(i)表示i二进制位中1的个数。然后考虑求和。
• 考虑把n的二进制中的1拆下来，那么剩下的位数就可以随便选。
  因此枚举一个固定的前缀，考虑当前情况下后半部分任意填写的方案数。
  假设后半部分长度为 L， 则有 k 个1的方案数为 $C_L^k$ ，统计贡献即可。
• 考虑再优化，因为一共n位, 在n位取小于等于n个1的方案数 $C_n^0\ast c_0+C_n^1\ast c_1+...+C_n^n\ast c_n=(c+1{)}^n$。
  所以当他最高位多了一位为1时，他的次方数就会变为x+1，也就是ans*c。
  当他最高位多了一位为0时，她就等价于上一位为满1的情况。
  所以$f[i]=f[i+1]\ast c+(c+1{)}^{len-i-1}$。
• 参考资料

#include<bits/stdc++.h>
using namespace std;
#define ios ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
const LL mod = 1e9+7;
LL mpow(LL a, LL x)  if(x==0)return 1; LL t = mpow(a, x>>1); if(x%2==0)return t*t%mod; return t*t%mod*a%mod; 
int main()
    string s;  LL c;  cin>>s>>c;
    LL ans = 1, len = s.size();
    for(int i = len-1; i >= 0; i--)
        if(s[i]=='1')
            ans = (mpow(c+1,len-i-1)+c*ans%mod)%mod;
        
    
    cout<<ans<<"\\n";
    return 0;

F.Strange Memory

F. Strange Memory
time limit per test1.0 s
memory limit per test256 megabytes
inputstandard input
outputstandard output
Once there was a rooted tree. The tree contained n nodes, which were numbered 1,…,n. The node numbered 1 was the root of the tree. Besides, every node i was assigned a number ai. Your were surprised to find that there were several pairs of nodes (i,j) satisfying
ai⊕aj=alca(i,j),
where ⊕ denotes the bitwise XOR operation, and lca(i,j) is the lowest common ancestor of i and j, or formally, the lowest (i.e. deepest) node that has both i and j as descendants.

Unfortunately, you cannot remember all such pairs, and only remember the sum of i⊕j for all different pairs of nodes (i,j) satisfying the above property. Note that (i,j) and (j,i) are considered the same here. In other words, you will only be able to recall
∑i=1n∑j=i+1nai⊕aj=alca(i,j).
You are assumed to calculate it now in order to memorize it better in the future.

Input
The first line contains a single integer n (2≤n≤105).

The second line contains n integers, a1,a2,…,an (1≤ai≤106).

Each of the next n−1 lines contains 2 integers u and v (1≤u,v≤n,u≠v), indicating that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output
Print what you will memorize in the future.

Example
inputCopy
6
4 2 1 6 6 5
1 2
2 3
1 4
4 5
4 6
outputCopy
18

题意：

• 给出一颗n个点的树，每个点有一个权值，计算下面这个式子的结果（即所有满足方括号中要求的点对，取下标值异或并累加）。
  
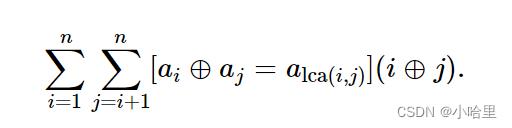
• n<1e5。

思路：

• 考虑暴力做法， 可以枚举每个点作为lca来计算贡献。
  对u子树内的点i，若其他子树内存在点j，满足$a_j=a_u\oplus a_i$，则点对i和j就可以产生贡献。
• 如何快速找到这样的点对（i,j）， 直接暴力n^2肯定会超时。可以拆位并开个哈希表记录一下。令$cnt[i][j][0/1]$表示当前子树内权值为 i 的节点中，二进制第 j 位有多少个节点是0/1。
• 那么就可以用dsu on tree模板来维护子树的信息，启发式合并，复杂度可以通过。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;

int n, a[maxn]; 
vector<int>G[maxn];
long long ans;

//轻重链剖分, dfs序
int dfn[maxn], low[maxn], num[maxn], id;
int siz[maxn], son[maxn];
void dfs(int u, int fa)
    siz[u] = 1;  dfn[u] = ++id;  num[id] = u;
    for(int to  : G[u])
        if(to==fa)continue;
        dfs(to, u);
        siz[u] += siz[to];
        if(siz[son[u]] < siz[to])son[u] = to;
    
    low[u] = id;


//dsu on tree, 维护当前权值为a[u]的节点中, 下标的二进制第i位有多少个0/1（拆位）
int cnt[1058576][25][2], SON;  //>2^20
void add(int u, int w) 
    for(int i = 0; i <= 20; i++)cnt[a[u]][i][(u>>i)&1] += w;

void del(int u)   
    for(int i = dfn[u]; i <= low[u]; i++)add(num[i], -1);

void calc(int u, int fa)
    add(u, 1);
    for(int to : G[u])
        if(to==SON || to==fa)continue;
        for(int j = dfn[to]; j <= low[to]; j++)  //枚举to的子树中的点x
            int x = num[j];
            for(int k = 0; k <= 20; k++)
                ans += 1ll*(1<<k)*cnt[a[u]^a[x]][k][1^((x>>k)&1)]; //x与其他非to子树构成的贡献
            
        
        for(int j = dfn[to]; j <= low[to]; j++)add(num[j], 1); //将to子树累加上去
    

void dsu(int u, int fa, int op)
    //轻链暴力
    for(int to : G[u])
        if(to!=son[u] && to!=fa)dsu(to, u, 0); //op=0表示递归完成后消除对该点的影响
    //重链启发式合并（轻链往重链上合并）
    if(son[u])dsu(son[u], u, 1), SON = son[u]; //统计重儿子的贡献，不消除影响
    //计算以u为lca的答案
    calc(u, fa);  SON = 0;
    if(!op)del(u);  //消除对该点的影响


int main()
    cin>>n;
    for(int i = 1; i <= n; i++)cin>>a[i];
    for(int i = 1; i < n; i++)
        int u, v;  cin>>u>>v;
        G[u].push_back(v);  G[v].push_back(u);
    
    dfs(1,1);
    dsu(1,1,0);
    cout<<ans<<"\\n";
    return 0;