QARepVGG：让RepVGG再次强大：一种量化感知的方法

Posted 2023-01-11 迪菲赫尔曼

性能和推理速度之间的权衡对于实际应用至关重要。而重参化可以让模型获得了更好的性能平衡，这也促使它正在成为现代卷积神经网络中越来越流行的架构。尽管如此，当需要INT8推断时，其量化性能通常太差，无法部署（例如ImageNet上的前1精度下降超过20%）。
在本文中深入探讨了这种失败的潜在机制，其中原始设计不可避免地扩大了量化误差。作者提出了一种简单、鲁棒和有效的量化友好型结构作为补救方法，该结构也享有重参化的好处，大大弥补了RepVGG的INT8和FP32精度之间的差距。没有任何花里胡哨的Trick，通过标准的训练后进行量化，便可以将在ImageNet上的Top-1精度下降控制在了2%以内。

---

1、简介

尽管深度神经网络在视觉、语言和语音方面取得了巨大成功，但模型压缩已变得非常必要，特别是考虑到数据中心功耗的巨大增长，以及全球范围内资源受限的边缘设备的大量分布。网络量化作为最成熟的方法之一，它具有较低的内存成本和固有的整数计算优势，因此研究模型的量化性能也是必不可少的操作。

然而，神经架构设计中的量化意识并不是优先考虑的问题，因此在很大程度上被忽视了。然而，如果量化是最终部署的强制操作，则可能会变得有害。例如，许多众所周知的体系结构都存在量化崩溃问题，如MobileNet和EfficientNet，这需要补救设计或高级量化方案。

最近，神经架构设计中最有影响力的方向之一是重参化。其中，RepVGG在训练期间将标准的Conv-BN-ReLU改造为其相同的多分支对应，这带来了强大的性能改进，同时不会增加额外的推理成本。由于其简单性和推理优势，它受到最近许多视觉任务的青睐。然而，基于重参化的模型面临众所周知的量化困难，这是阻碍行业应用的内在缺陷。事实证明，使这种结构顺利地量化是非常重要的。标准的训练后量化方案极大地降低了RepVGG-A0的精度，从72.4%降至52.2%。同时，应用量化感知训练并不简单。

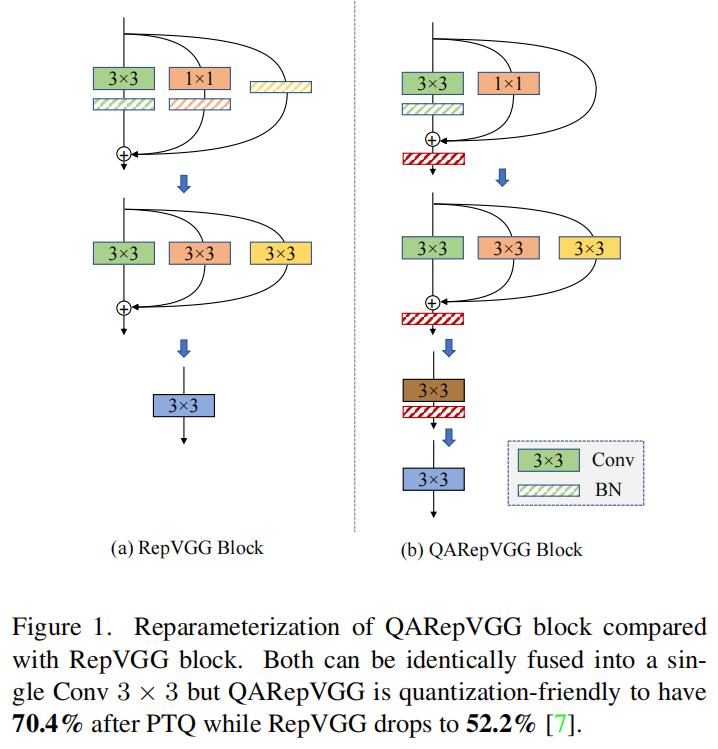
这里，特别关注RepVGG的量化难度。为了解决这个问题，作者深入分析了基于重参化的典型架构的基本量化原则。也就是说，为了使网络具有更好的量化性能，权重的分布以及任意分布的处理数据应该是量化友好的。两者对于确保更好的量化性能至关重要。更重要的是，这些原则将我们引向一种全新的设计，作者称之为QARepVGG（Quantization Aware RepVGG），它不会遭受实质性的量化崩溃，其构建块如图1所示，其量化性能得到了很大改善。

本文的贡献有3点：

1. 揭示了基于重参化的架构（如RepVGG）量化中性能崩溃的根本原因。

2. 设计了RepVGG的量化友好模块（即QARepVGG），该模块在权重和激活分布方面保持基本差异，同时保持突出速度和性能权衡的优势。

3. 本文提出的方法在不同的模型尺度和不同的视觉任务上得到了很好的推广，实现了可以部署的出色的后量化性能。此外，提出的模型在FP32精度方面与RepVGG相当。

2、相关方法

2.1、Reparameterization Architecture Design

RepVGG在训练阶段以多个分支的形式进行的，并在推理过程中将多个分支融合成一个分支，这个融合的过程被称为重参化。后续的工作DBBNet和MobileOne通过引入多样化的组合来扩展了这种设计，增强了性能和延迟之间的权衡。这种重参化的趋势也适用于最近的目标检测方法，如PPYOLO-E、YOLOv6和YOLOv7。

2.2、Quantization

量化是一种有效的模型压缩方法，它将网络权重和输入数据映射到较低精度（通常为8位）以进行快速计算，这大大降低了模型大小和计算成本。在不影响性能的情况下，在部署之前，大多采用量化来提高速度，这是工业生产中的事实标准。

训练后量化（PTQ）是最常见的方案，因为它只需要几批图像来校准量化参数，并且不需要额外的训练。还提出了量化感知训练（QAT）方法来提高量化精度，例如仅整数算术量化、无数据量化、硬件感知量化、混合精度量化以及零样本量化。由于QAT通常涉及到对训练代码的开发，并且需要额外的成本，因此仅当训练代码在手边并且PTQ不能产生令人满意的结果时才使用QAT。为了最好地展示所提出的量化感知架构，作者主要使用PTQ评估量化精度。同时，还通过实验证明了它对QAT也是有益的。

2.3、Quantization-aware architecture design

在《A quantization-friendly separable convolution for mobilenets》中提出了一种量化友好的可分离卷积替换方法，其中定义了一种称为信噪比（SQNR）的度量来诊断网络各组成部分的量化损失。它还认为，权重应服从均匀分布，以促进量化。

众所周知，Swish-like激活会带来量化崩溃，这要么是需要一个精细的可学习的量化方案来恢复，要么是被RELU-6取代，就像EffificientNet-Lite一样。

BatchQuant利用一次性神经结构搜索鲁棒混合精度模型，无需再训练。

2.4、Quantization for Reparameterization Network

基于重参化的架构由于其固有的多分支设计而增加了动态数值范围，因此存在量化困难。通过PTQ使重参化模型的精度下降是不可接受的。由于部署模式下的重参化网络缺乏BN层，因此使用QAT难以提高量化精度。

据作者描述，RepOpt-VGG是唯一一个通过构建一个两阶段的优化管道来努力解决这个量化问题的相关工作。RepOpt-VGG认为量化困难是由于fused kernels的量化参数分布造成的。

本文作者重新研究了这个问题，发现它要复杂得多，而且巨大的量化误差是权重和激活的协同效应的结果。

3、本文方法

一些源可能会在标准量化管道QAT中引入误差。作者选择均方误差（MSE）作为Hptq之后的度量来度量一个张量的量化误差，
$$\mathrm{MSE}\left(Q\left(\mathbf{w},t,n_b\right),\mathbf{w}\right)=\frac{1}{n}\sum _i{\left(Q\left({\mathbf{w}}_i,t,n_b\right)-\mathbf{w}\right)}^2$$
其中Q为量化过程，$w\in R^n$为n个通道的权值，一个阶段阈值$t$，$n_b$为位宽。具体的量化误差由张量分布的几个因素决定，包括最大值和最小值、标准偏差、阶段阈值等。不幸的是，作者也不能给出一个具体的解，因为不能假设网络中张量的任何分布。在实践中认为一个量化友好的分布是一个具有相对较小的数值范围和一个较小的标准偏差的分布。

对于基于重参化的体系结构，有两个主要组件，权重和激活，它们需要量化，并可能导致精度下降。激活也可以作为下一层的输入，误差会逐步增加累积。因此，神经网络良好的量化性能主要需要两个基本条件：

• C1：权重分布有利于量化

• C2：激活分布（即模型如何响应输入特征）易于量化

根据经验，违反其中任何一种都会导致较低的量化性能。以RepVGG-A0为例，研究了为什么基于重参化的结构的量化是困难的。

3.1、深入探讨重参化结构的量化失效问题

作者首先用RepOpt的代码再现了RepVGG-A0的性能，如表1所示。在此基础上可以进一步控制实验设置。作者用PTQ的标准设置对RepVGG-A0进行量化，并评估INT8的准确性，从72.2%下降到了50.3%。

请注意，在融合多分支后使用已部署的模型，因为未融合的模型会导致额外的量化误差。这个Trick在流行的量化框架中被广泛使用。

在图2和图14a（附录）中说明了RepVGG-A0的权重分布。观察到权值在0附近分布得很好，并且不存在特定的离群值，因此它满足C1。这导致我们验证c2，如果它是激活，极大地恶化了量化。

不幸的是，激活是输入依赖的，并通过卷积与学习到的权值相结合。从理论上讲，通过假设输入和权重的任何分布来得出一些结论是很重要的。相反，可以相对地分析每个分支的标准差。

为了更好地理解，作者保持了与RepVGG相同的命名。具体来说，使用$W_{(k)}\in R^{C_2\times C_1\times k\times k}$来表示$k\times k$卷积的kernel，其中$C_1$和$C_2$分别是输入和输出通道的数量。注意，$k\in 1,3$为RepVGG的配置。对于$k\times k$卷积后的批归一化（BN）层，使用${\mu }_{(k)}\in R^{C_2}$、${\sigma }_{(k)}\in R^{C_2}$、${\gamma }_{(k)}\in R^{C_2}$、${\beta }_{(k)}\in R^{C_2}$作为平均值、标准差、比例因子和偏差。对于恒分式分支中的BN，使用${\mu }_{(0)}$、${\sigma }_{(0)}$、${\gamma }_{(0)}$、${\beta }_{(0)}$。

设$M_{(1)}\in R^{N\times C_1\times H_1\times W_1}$，$M_{(2)}\in R^{N\times C_2\times H_2\times W_2}$分别为输入和输出，“∗”为卷积运算符。设$Y_{(0)}$、$Y_{(1)}$和$Y_{(3)}$为Idnetity、1×1和3×3分支的输出。不失一般性，假设$C_1=C_2$，$H_1=H_2$，$W_1=W_2$。然后可以将输出值$M_{(2)}$写成:
M ( 2 ) = Y ( 3 ) + Y ( 1 ) + Y ( 0 )