一文彻底搞定二叉树的前序中序后序遍历(图解递归非递归)

Posted 2023-01-11 Big sai

前言

大家好，我是bigsai，在数据结构与算法中，二叉树无论是考研、笔试都是非常高频的考点内容，在二叉树中，二叉树的遍历又是非常重要的知识点，今天给大家讲讲二叉树的层序遍历。

这部分很多人可能会但是需要注重一下细节。

前面介绍了二叉排序树的构造和基本方法的实现，遍历也是比较重要的一环，并且二叉树的层序遍历也是bfs的最简单情况，这里我就将二叉树的层序遍历以及常考问题给大家分享一下。

在了解二叉树的遍历之前，需要具备数据结构与算法有队列、递归、栈、二叉树，这些内容咱们前面都有讲过，有这方面知识欠缺的同学可以往前翻一翻看一看！

层序遍历

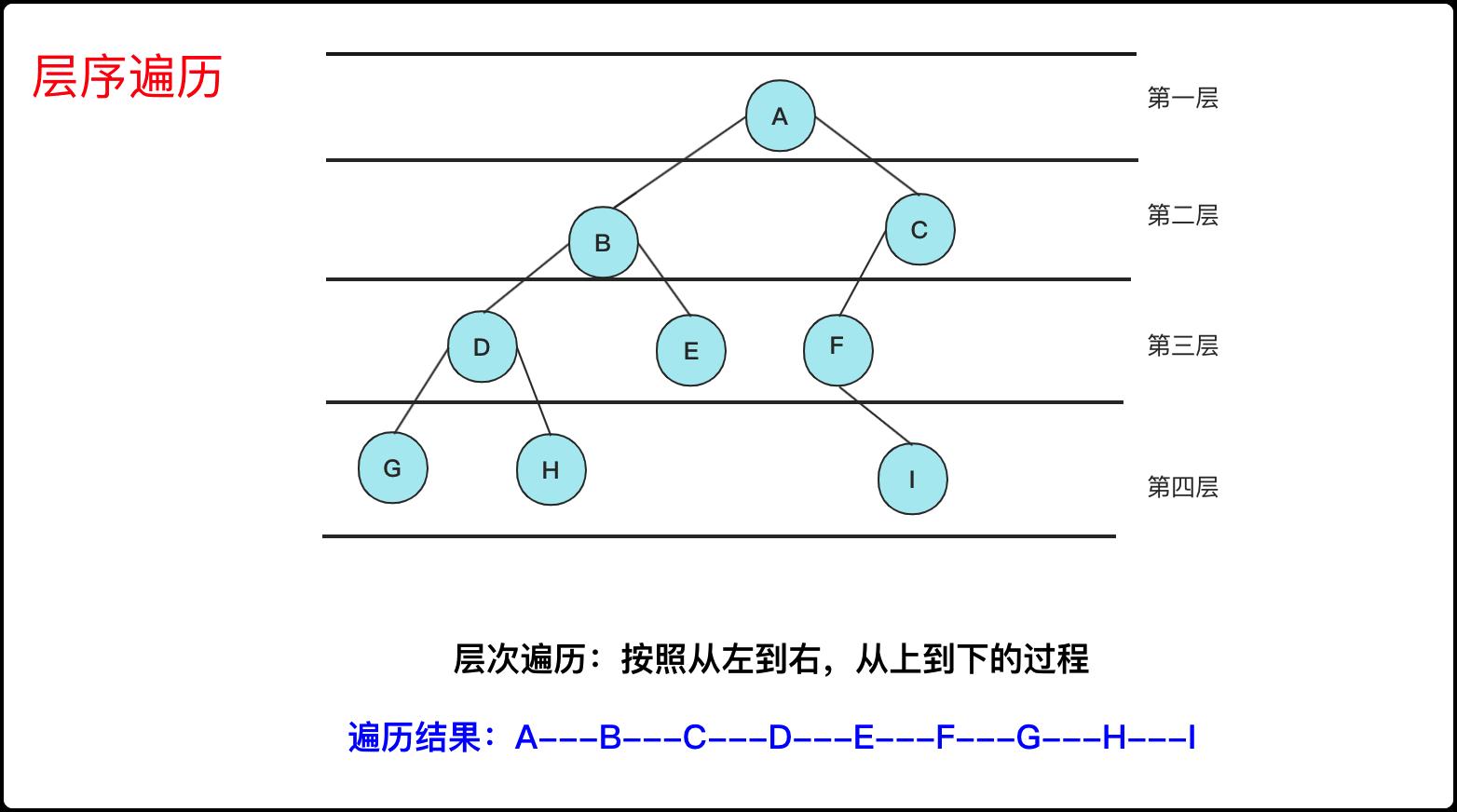
层序遍历，听名字也知道是按层遍历。一个节点有左右节点，按层处理就是当前层兄弟节点的优先级要大于子节点处理的优先级，所以就是要将子节点放到后面处理，这就适合队列这个数据结构用来存储。

对于队列，先进先出。从root节点push到队列，那么队列中先出来的顺序是第二层的左右(假设都有)，第二层每个节点执行的时候按照左右顺序添加到队列，第三层的节点就会有序的放到最后面……按照这样的规则就能得到一个层序遍历的顺序。

实现的代码也很容易理解：

public int[] levelOrder(TreeNode root) 
        int arr[]=new int[10000];
        int index=0;
        Queue<TreeNode>queue=new ArrayDeque<>();
        if(root!=null)
            queue.add(root);
        while (!queue.isEmpty())
            TreeNode node=queue.poll();
            arr[index++]= node.val;
            if(node.left!=null)
                queue.add(node.left);
            if(node.right!=null)
                queue.add(node.right);
            
        
        return Arrays.copyOf(arr,index);
    

分层存储

但是在具体笔试他可能要求你分层存储，例如力扣的102二叉树的层序遍历，要求返回一个List<List<Integer>>类型。

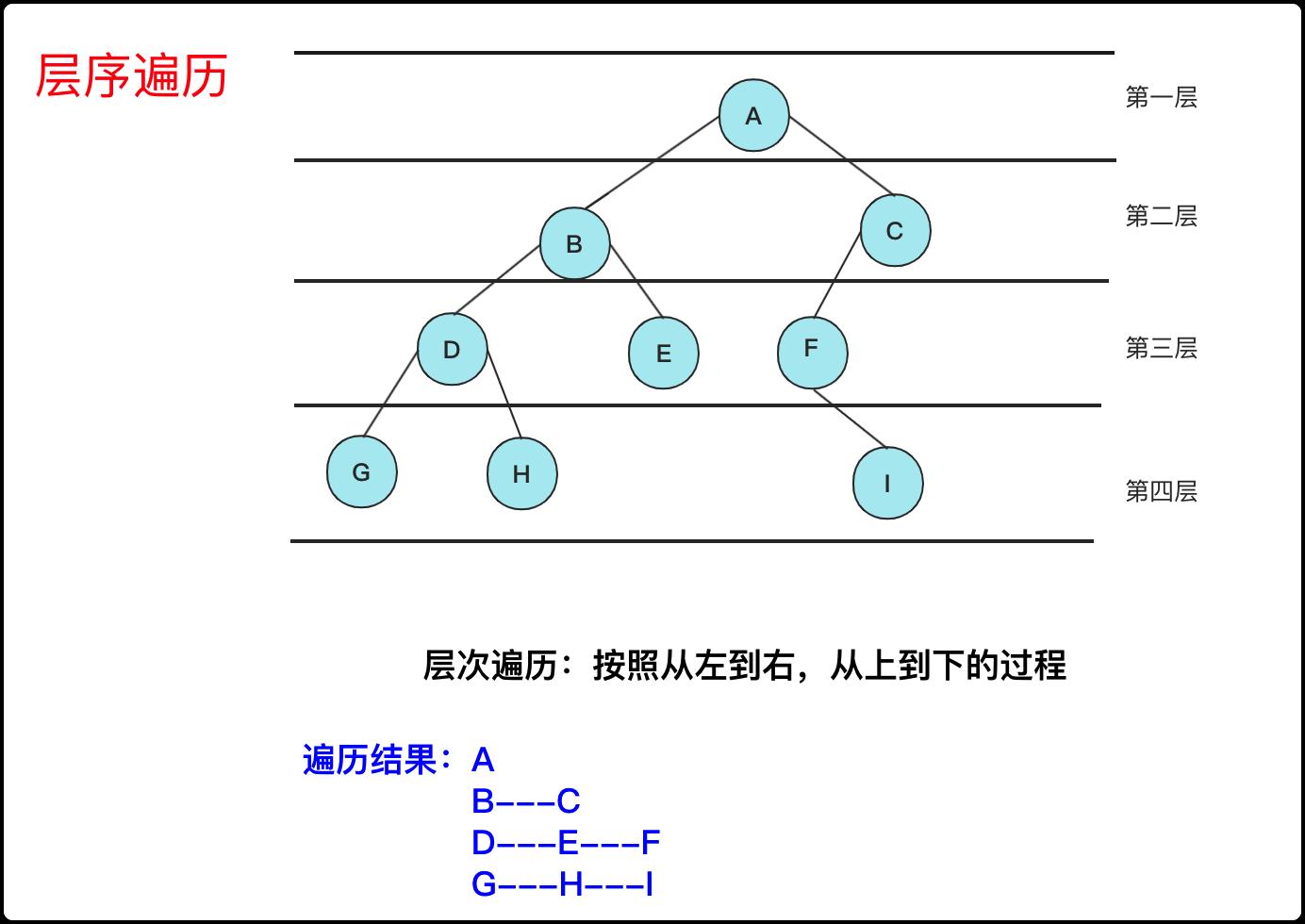
这种相比上面一个多了一层逻辑就是每一层数据放到一块，这个也很容易，最好想到的就是两个队列(容器)一层一层遍历存储，然后交替，但是两个队列(容器)的写法常常会被面试官嫌弃，很多面试官让你想想怎么不用两个容器实现？

不用双队列去枚举结果也很容易，重要的就是先记录队列大小size(当前层节点数量)，然后执行size次数的枚举即可，具体代码为：

public List<List<Integer>> levelOrder(TreeNode root) 
  List<List<Integer>>list=new ArrayList<List<Integer>>();
  if(root==null)return list;
  Queue<TreeNode>q1=new ArrayDeque<TreeNode>();
  q1.add(root);
  while (!q1.isEmpty()) 
    int size=q1.size();
    List<Integer>value=new ArrayList<Integer>();
    for(int i=0;i<size;i++)
    
      TreeNode pNode=q1.poll();
      if(pNode.left!=null)
        q1.add(pNode.left);
      if(pNode.right!=null)
        q1.add(pNode.right);
      value.add(pNode.val);
    
    list.add(value);
  
  return list;

之字形打印

除了这个直接层序遍历，二叉树还有很高频的就是之字形遍历，例如剑指offer32和力扣103 二叉树的锯齿形层序遍历，它的题目要求为：

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

这道题虽然不是难题，但是有点绕，本来队列这玩意我们就要大脑想一下什么顺序，又出来一个之字形，属实增加的思维逻辑，有不少小伙伴反映当时面试官让手撕这道题，自己以前明明写过，但是太紧张自己给自己绕进去了！

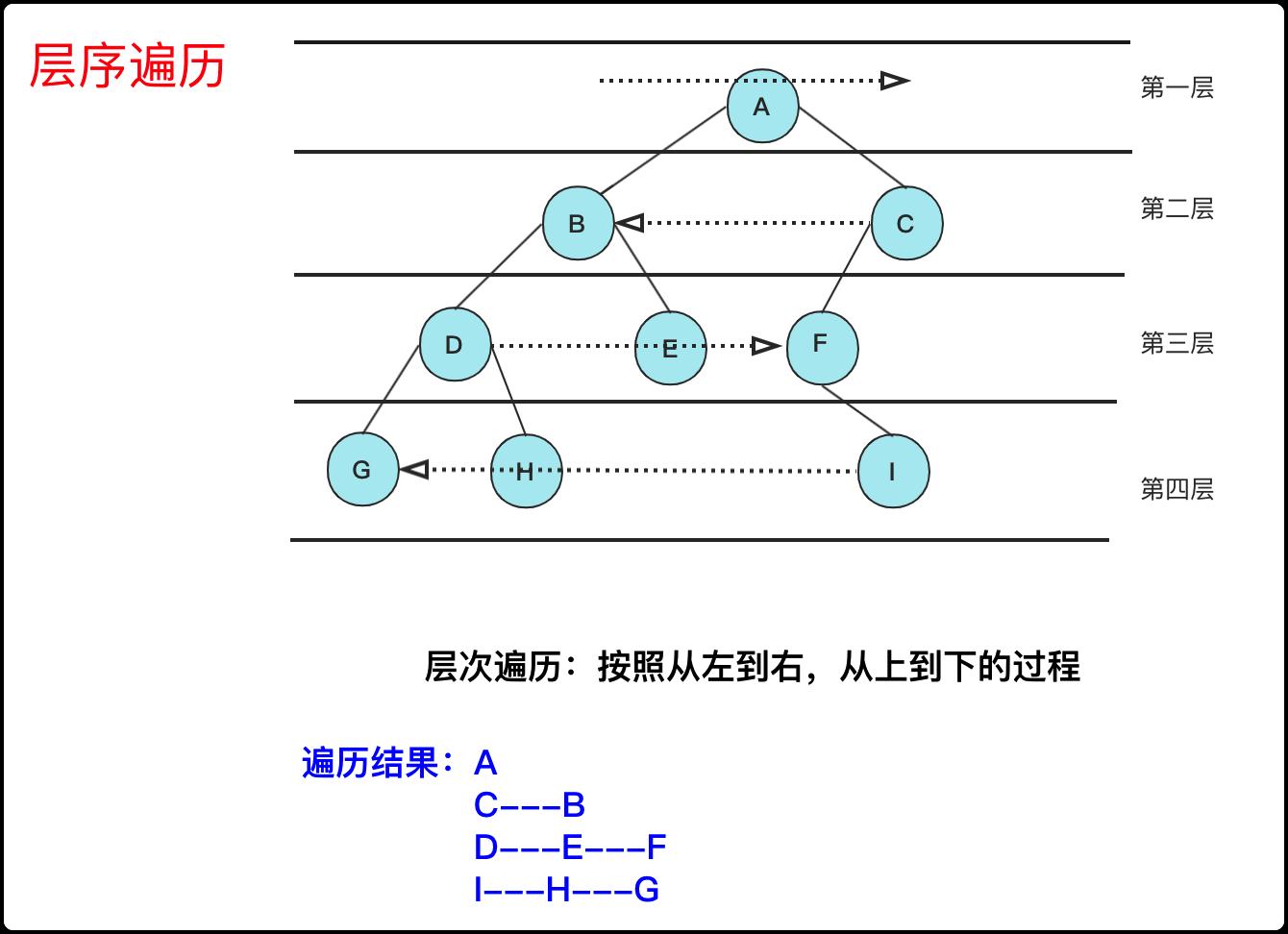
其实这个问题也很容易转化，因为值只是存储，我们按照老样子去进行层序遍历，只不过在遍历时候通过当前层奇偶数来给它判断是从左往右存储到结果中还是从右往左放到结果中。当然，判断奇数偶数也很容易，可以用变量，也可以用结果List的size()都可。

个人实现的一个朴素代码为：

public List<List<Integer>> levelOrder(TreeNode root) 
  List<List<Integer>> value=new ArrayList<>();//存储到的最终结果
  if(root==null)
    return value;
  int index=0;//判断
  Queue<TreeNode>queue=new ArrayDeque<>();
  queue.add(root);
  while (!queue.isEmpty())
    List<Integer>va=new ArrayList<>();//临时 用于存储到value中
    int len=queue.size();//当前层的数量
    for(int i=0;i<len;i++)
      TreeNode node=queue.poll();
      if(index%2==0)
        va.add(node.val);
      else
        va.add(0,node.val);
      if(node.left!=null)
        queue.add(node.left);
      if(node.right!=null)
        queue.add(node.right);
    
    value.add(va);
    index++;
  
  return value;

上面实现代码也仅使用一个队列，不过这个问题可能有很多更巧妙的解法需要大家自己去挖掘。

结语

二叉树的层序遍历是二叉树内容中较为简单的内容，但是层序遍历尤其是之字形遍历(锯齿形遍历)出现的频率真的太高了，并且最好是掌握比较好的方法不要显得太臃肿。

不过在实际遇到问题时候，能AC是第一位，然后才是精简的逻辑和骚气的代码。

二叉树层序遍历变种问题不多，掌握上面三个问题基本就够了，而二叉树的前序、中序、后序遍历(递归非递归)考察非常多，后面会给大家加快梳理总结，敬请期待！

最后给大家分享一波大漠风光！

前言

大家好，我是bigsai，好久不见，甚是想念！

今天带大家征服二叉树的前中后序遍历，包含递归和非递归方式，学到就是赚到！

很多时候我们需要使用非递归的方式实现二叉树的遍历，非递归枚举相比递归方式的难度要高出一些，效率一般会高一些，并且前中后序枚举的难度呈一个递增的形式，非递归方式的枚举有人停在非递归后序，有人停在非递归中序，有人停在非递归前序(这就有点拉胯了啊兄弟)。

我们回顾递归，它底层其实是维护一个栈，将数据存到栈中，每次抛出栈顶的数据进行处理(也就是递归、dfs的方向化、极端化枚举特征非常明显)，我们驾驭递归的时候更重要的是掌握上下层之间的逻辑关系。

而非递归方式我们除了需要掌握上下层的逻辑关系之外，要手动的处理各种条件变更的细节， 递归是一个一来一回的过程，如果我们的逻辑只是在单趟的来或者回中还好，有时候甚至要自己维护来和回的状态，所以逻辑上难度还是比较大的。

二叉树的前序遍历

二叉树的前序遍历是最简单的，其枚举方式就是一个最简单的dfs，学会了二叉树的前序遍历，那么后面入门dfs就容易很多。

二叉树的前序遍历的枚举规则为：根结点 —> 左子树 —> 右子树，也就是给定一棵树，输出操作当前节点，然后枚举左子树(左子树依然按照根左右的顺序进行)，最后枚举右子树(右子树也按照根左右的顺序进行)，这样得到的一个枚举序列就是二叉树的前序遍历序列(也叫先序)。

前序遍历在二叉树树的顺序可以看下图(红色箭头指向的表示需要访问的，可以看出从父节点枚举下来第一次就要被访问)。

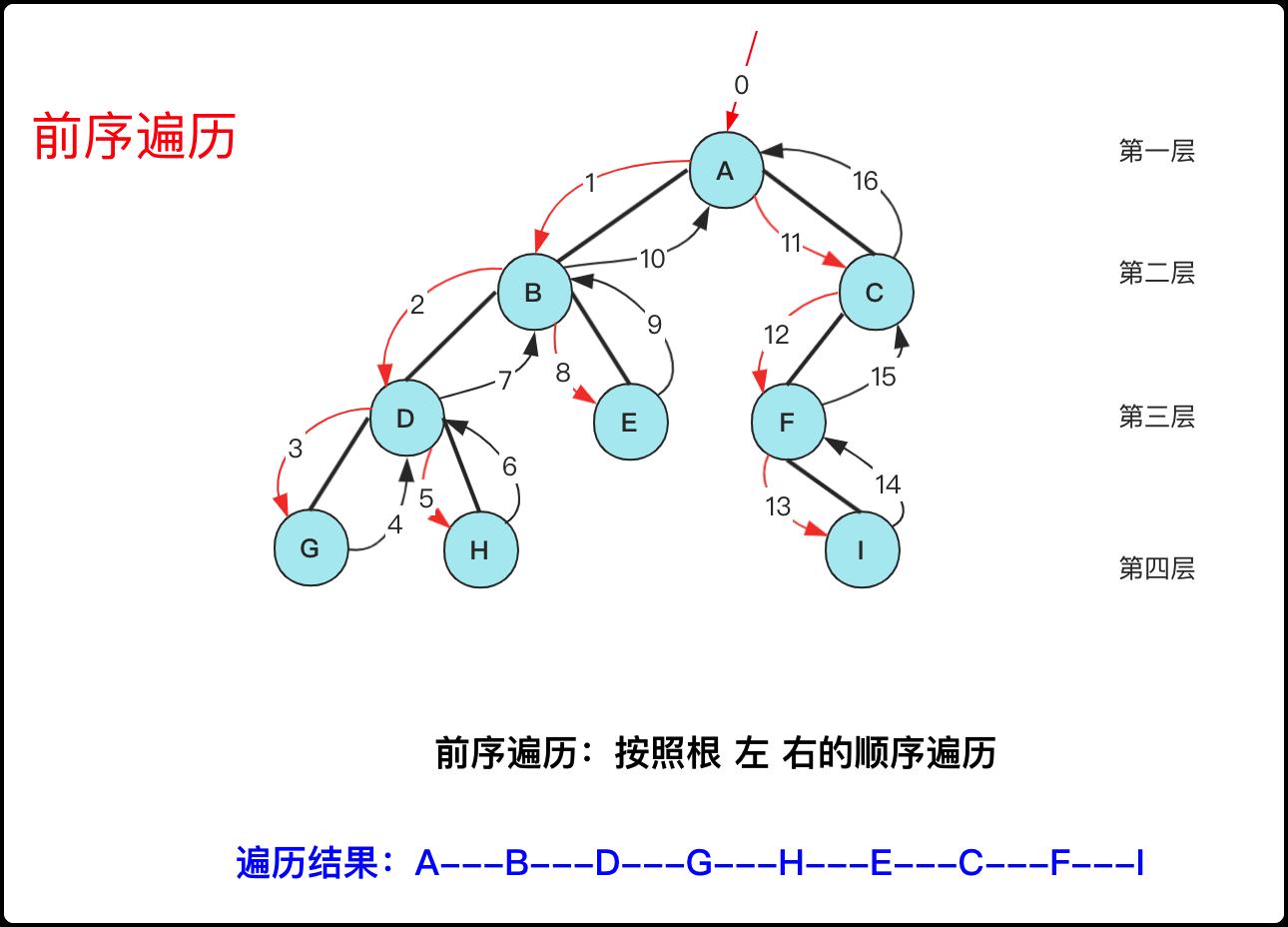
在具体实现的方式上，有递归方式和非递归方式实现。

递归

递归方式实现的二叉树前序遍历很简单，递归我们只需要考虑初始情况、结束边界、中间正常点逻辑。

初始情况：从root根节点开始枚举，函数执行传入root根节点作为参数。

结束边界：节点的左(或右)子节点为null那么就停止对应节点的递归执行。

正常点逻辑：先处理当前点(存储或输出)，递归调用枚举左子树(如果不为null),递归调用枚举右子树(如果不为null)。

刚好力扣144二叉树的前序遍历可以尝试ac：

class Solution 
    List<Integer>value=new ArrayList();
    public List<Integer> preorderTraversal(TreeNode root) 
        qianxu(root);
        return value;
    
    private void qianxu(TreeNode node) 
        if(node==null)
            return;
        value.add(node.val);
        qianxu(node.left);
        qianxu(node.right);
    

非递归

非递归的前序还是非常简单的，前序遍历的规则是：根节点，左节点，右节点。但是根左方向一直下去，手动枚举又没有递归回的过程，一直下去我们怎么找到回来时候的右几点呢？

用栈将路过的节点先存储，第一次枚举节点输出储存然后放入栈中，第二次就是被抛出时候枚举其右侧节点。

它的规则大致为：

1. 一直访问当前节点并用栈存储，节点指向左节点，直到左孩子为null。

2. 抛出栈顶不访问。如果有右节点，访问其右节点重复步骤1，如有没右节点，继续重复步骤2抛出。

这样的一个逻辑，就会从根出发一直先往左访问，访问结束根、左之后再访问右节点(子树)，得到一个完成的前序遍历的序列。

具体实现的代码为：

class Solution 
  public List<Integer> preorderTraversal(TreeNode root) 
    List<Integer>value=new ArrayList();
    Stack<TreeNode> q1 = new Stack();	
		while(!q1.isEmpty()||root!=null)
		
			while (root!=null) 
				value.add(root.val);
				q1.push(root);				
				root=root.left;
			
            root=q1.pop();//抛出
            root=root.right;//准备访问其右节点
			
		
        return value;
    

二叉树的中序遍历

二叉树的中序遍历出现的频率还是蛮高的，如果是二叉排序树相关问题还是蛮多的，你要知道二叉排序树的中序遍历是一个有序的序列，如果求二叉排序树的topk问题，非递归中序那效率是非常高的。

中序遍历在二叉树树的顺序可以看下图(红色箭头指向的表示需要访问的，可以看出如果子树为null，那肯定要访问，否则就是从左子树回来的时候才访问这个节点)。

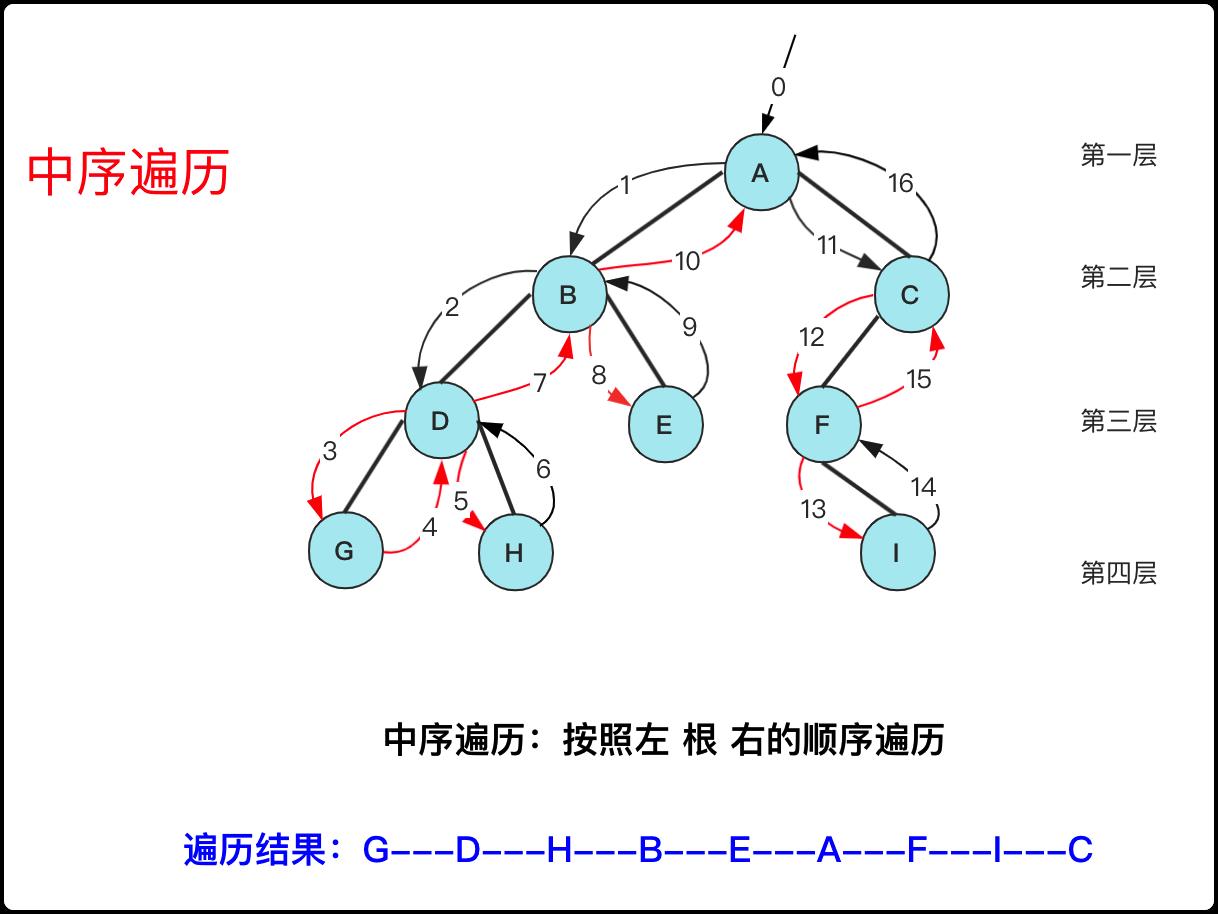
递归方式

递归方式实现很简单，其逻辑和前序递归相似的，力扣94刚好有二叉树中序遍历,这里我直接放代码：

class Solution 
   public List<Integer> inorderTraversal(TreeNode root) 
	  List<Integer>value=new ArrayList<Integer>();
	  zhongxu(root,value);
	  return value;
  
	 private void zhongxu(TreeNode root, List<Integer> value) 
		 if(root==null)
			 return;
		 zhongxu(root.left, value);
		 value.add(root.val);
		 zhongxu(root.right, value);
		
	

非递归方式

非递归的中序和前序是非常相似的，前序遍历的规则是：根节点，左节点，右节点。中序遍历的顺序是左节点，根节点，右节点 ，在前序中先根后左其实是有点覆盖的关系(这个左就是下一个跟)，在其非递归枚举实现上我们访问右节点时候是先抛出父节点不访问，直接访问父节点的右节点，如果抛出父节点访问这个父节点，其实它就是一个中间顺序的节点。

它的规则大致为：

1. 枚举当前节点(不存储输出)并用栈存储，节点指向左节点，直到左孩子为null。

2. 抛出栈顶访问。如果有右节点，访问其右节点重复步骤1，如有没右节点，继续重复步骤2抛出。

这样的一个逻辑，就会形成一个中序序列，因为叶子节点的左右都为null，这样的规则依然满足中序。

实现代码为：

class Solution 
   public List<Integer> inorderTraversal(TreeNode root) 
	List<Integer>value=new ArrayList<Integer>();
    Stack<TreeNode> q1 = new Stack();	
    while(!q1.isEmpty()||root!=null)
    
        while (root!=null) 
            q1.push(root);				
            root=root.left;
        
        root=q1.pop();//抛出
        value.add(root.val);
        root=root.right;//准备访问其右节点
        
    
    return value;
  

二叉树的后序遍历

二叉树的后序遍历非递归方式实现起来难度最大的，能够手写非递归后序，一定能亮瞎面试官的眼！

后序遍历在二叉树树的顺序可以看下图(红色箭头指向的表示需要访问的，可以看出如果子树为null，那肯定要访问，否则就是从右子树回来的时候才访问这个节点)。

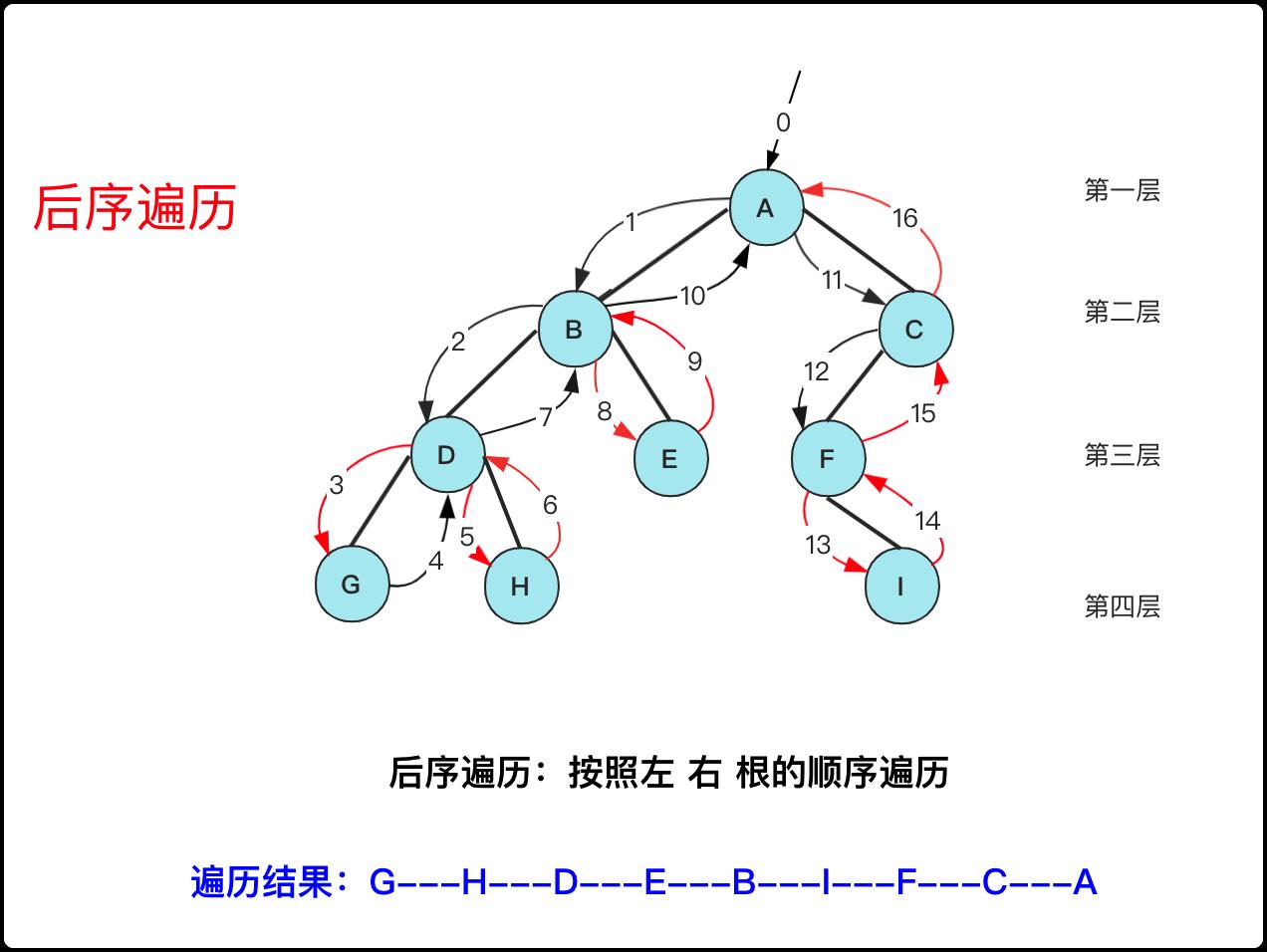
递归

二叉树递归方式后序遍历很简单，跟前序中序的逻辑一样，在力扣145有后序的code测试大家可以自己尝试一下。

这里直接放我写的后序递归方式：

class Solution 
    List<Integer>value=new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) 
        houxu(root);
        return value;
    
    private void houxu(TreeNode root) 
        if(root==null)
            return;
        houxu(root.left);
        houxu(root.right);//右子树回来
        value.add(root.val);
    

非递归

非递归的后序就稍微难一点了，大家可以回顾一下二叉树的前序和中序遍历，其实都是只用一个栈直接抛出就可以找到右节点，抛出后栈就空了，但是这个后序遍历的顺序是 左子树 —> 右子树 —>根节点，也就是处理完右节点，还要再回到根节点访问。所以从逻辑结构上和前序、中序的非递归实现方式有一些略有不同。

前序，中序遍历的顺序提取为：

前序: 中入栈——>左入栈——>左孩子入出——>左出栈——>中出栈——>右入栈——>右孩子入出——>右出栈

前序遍历按照入栈顺序即形成一个前序序列

中序: 中入栈——>左入栈——>左孩子入出——>左出栈——>中出栈——>右入栈 ——>右孩子入出——>右出栈

中序遍历按照出栈顺序即形成一个中序序列

但是后序的话应该怎么考虑呢？

其实就是在从左孩子到中准备出栈的时候，先不出栈记成第一次，再将它放入栈中，如果从右孩子返回那么这个节点就是第三次遍历(第一次访问中，然后枚举左返回第二次，枚举右返回第三次)，这时候将其抛出就形成一个后序。

如果不理解这里画了一个简单的图帮助理解：

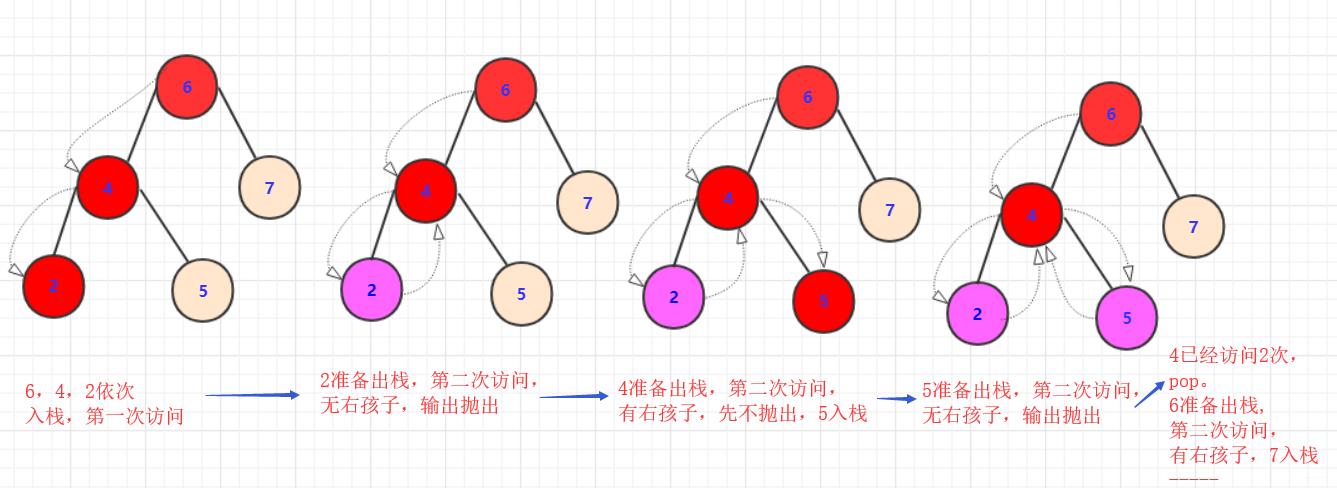
思路理解了，怎么实现呢？最简单的就是使用一个hashmap存储节点访问次数。

附一下个人实现的代码：

class Solution 
    public List<Integer> postorderTraversal(TreeNode root) 
        List<Integer> value=new ArrayList();
        Stack<TreeNode> q1 = new Stack();	
        Map<TreeNode,Integer >map=new HashMap<>();
        while(!q1.isEmpty()||root!=null)
        
            if (root!=null) 
                q1.push(root);
                map.put(root, 1); //t.value标记这个值节点出现的次数
                root=root.left;
            
            else 
                root=q1.peek();
                if(map.get(root)==2) //第二次访问，抛出
                    q1.pop();
                    value.add(root.val);
                    root=null;//需要往上走
                
                else 
                    map.put(root, 2);
                    root=root.right;
                     
            
          
          return value;
    

但是这个情况如果面试官问你如果有hash冲突怎么办？虽然这种概率非常小几乎不会但是面试官不会放过你，但是还是要用正统方法来实现。

那么正统方法怎么解决呢？

也很容易，用一个pre节点一直保存上一次抛出访问的点，如果当前被抛出的右孩子是pre或者当前节点右为null，那么就将这个点抛出，否则就将它"回炉重造"一次！

实现代码为：

class Solution 
    public List<Integer> postorderTraversal(TreeNode root) 
        TreeNode temp=root;//枚举的临时节点
        List<Integer>value=new ArrayList<>();
        TreeNode pre=null;//前置节点
        Stack<TreeNode>stack=new Stack<>();

        while (!stack.isEmpty()||temp!=null)
        
            while(temp!=null)
                stack.push(temp);
                temp=temp.left;
            
            temp=stack.pop();
            if(temp.right==pre||temp.right==null)//需要弹出
            
                value.add(temp.val);
                pre=temp;
                temp=null;//需要重新从栈中抛出
            else
                stack.push(temp);
                temp=temp.right;
            
            
        
        return value;
    

是不是觉得非常巧妙？那我再说一种骚操作的代码，你看 左右中，它反过来就是中右左，这不就是一个反的前序遍历嘛！所以进行一次反的前序遍历，然后将结果翻转一下也能得到这个值啦，当然，你使用双栈同时翻转也是一样的道理！

实现代码为：

class Solution 
    public List<Integer> postorderTraversal(TreeNode root) 
      List<Integer>value=new ArrayList();
      Stack<TreeNode> q1 = new Stack();	
      while(!q1.isEmpty()||root!=null)
      
        while (root!=null) 
          value.add(root.val);
          q1.push(root);				
          root=root.right;
        
      
以上是关于一文彻底搞定二叉树的前序中序后序遍历(图解递归非递归)的主要内容，如果未能解决你的问题，请参考以下文章
 
 二叉树的前序中序后序遍历相互求法
 二叉树的前序中序后序层次遍历的递归与非递归实现
 二叉树的前序中序后序层次遍历的递归与非递归实现
 二叉树的前序中序后序遍历
 非递归遍历二叉树的前序中序后序
 二叉树的前序中序后序遍历-非递归-使用同一段代码实现