汉诺塔（Hanoi）图解递归算法

Posted 2022-12-28 bfhonor

汉诺塔（Hanoi）

• 编程实现把 A 的 n 个盘子移动到 C（盘子编号是 [1, n] ）
  每次只能移动1个盘子
  大盘子只能放在小盘子下面
  

1、汉诺塔 — 1个盘子

2、汉诺塔 — 2个盘子

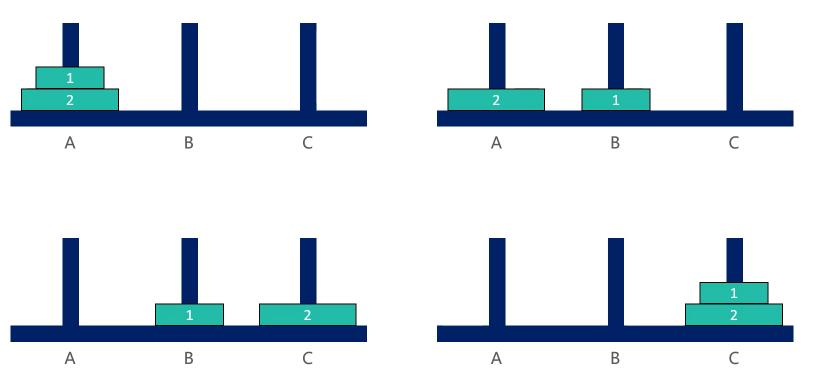
3、汉诺塔 — 3个盘子

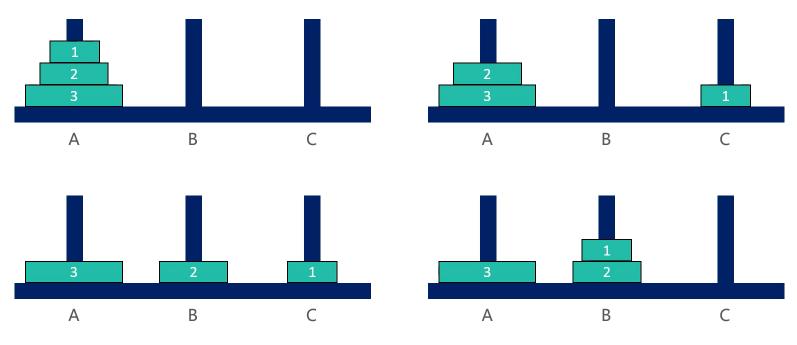
3、汉诺塔 — 思路

• 其实分 2 种情况讨论即可
  （1）当 n == 1时，直接将盘子从 A 移动到C
  （2）当 n > 1时，可以拆分成3大步骤
  ①将 n– 1 个盘子从 A 移动到B
  
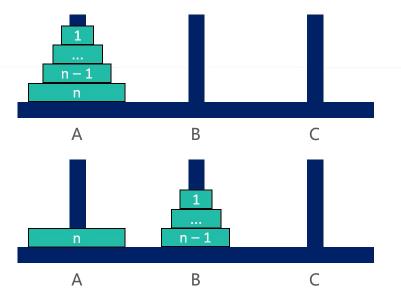
  ② 将编号为 n 的盘子从 A 移动到C
  
  ③将 n– 1 个盘子从 B 移动到C
  
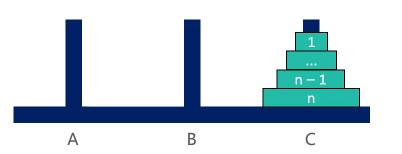
  ✓ 步骤①③ 明显是个递归调用

4、汉诺塔 — 实现

public class Hanoi 
    public static void main(String[] args) 
        new Hanoi().hanoi(3,"A","B","C");
    

    /**
     * 将n个碟子从p1挪动到p3
     * @param p2 中间的柱子
     */
    void hanoi(int n,String p1,String p2,String p3)
        if (n == 1)
            move(n,p1,p3);
            return;
        

        //将p3看作中间柱子，将n-1个碟子从p1移动到p2
        hanoi(n-1,p1,p3,p2);
        move(n,p1,p3);
        //将p1看作中间柱子，将n-1个碟子从p2移动到p3
        hanoi(n-1,p2,p1,p3);
    

    /**
     * 将 no号盘子从 from 移动到 to
     * @param no 碟子
     * @param from 开始移动的柱子
     * @param to 移动到的柱子
     */
    void move(int no, String from,String to)
        System.out.println("将"+no + "号盘子从" + from + "移动到"+to);
    

运行结果：
将1号盘子从A移动到C
将2号盘子从A移动到B
将1号盘子从C移动到B
将3号盘子从A移动到C
将1号盘子从B移动到A
将2号盘子从B移动到C
将1号盘子从A移动到C

• T(n) = 2 ∗ T(n) − 1 + O(1)
  因此时间复杂度是：O(2ⁿ)
• 空间复杂度：O(n)