图的应用(校园导航图最短路径求解)
Posted ଳxin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图的应用(校园导航图最短路径求解)相关的知识,希望对你有一定的参考价值。
博主个人网站:39.106.201.180/ccb
联系博主(VX):xincsc0731
一、实验要求:
设计四川轻化工大学的校园平面图,所含景点不少于8个。以图中顶点表示学校内各景点,存放景点的名称、景点介绍信息等;以边表示路径,存放路径长度信息。要求将这些信息保存在文件graph.txt中,系统执行时所处理的数据要对此文件分别进行读写操作。
1.从文件graph.txt中读取相应数据, 创建一个图,使用邻接矩阵表示图(算法6.1);
2.景点信息查询:为来访客人提供校园任意景点相关信息的介绍;
3.问路查询:为来访客人提供校园任意两个景点之间的一条最短路径(算法6.10)。
选做内容(对文件进行操作,相应信息变化后,再次进行景点信息查询和问路查询时应该有所体现)
- 修改一个已有景点的相关信息;
- 增加一个新景点及其相关信息;
- 增加一条新的路径;
- 删除一个景点及其相关信息;
- 删除一条路径。
实现提示: - 校园道路是双向通行的,可设校园平面图是一个带权的无向图,用邻接矩阵表示此无向网。
typedef struct
char name[100];
char info[10000];
VertexType; //顶点结构
typedef struct
VertexType vexs[10];
int arcs[100][100];//邻接矩阵
int vexnum,arcnum;//顶点个数,边的个数
MGraph; //图结构
2. 将图的顶点信息和边的信息用数据文件graph.txt存储,数据文件格式可以设置如下形式:
图中顶点数 边的数目
景点名称 景点信息
始点 终点 路径长度
如可以在文件graph.txt中存储以下数据:
8 15
品正食府 食堂,有美食
器美园 一期食堂,味道好
……
品正食府 东门 100
东南门 品正食府 400
……
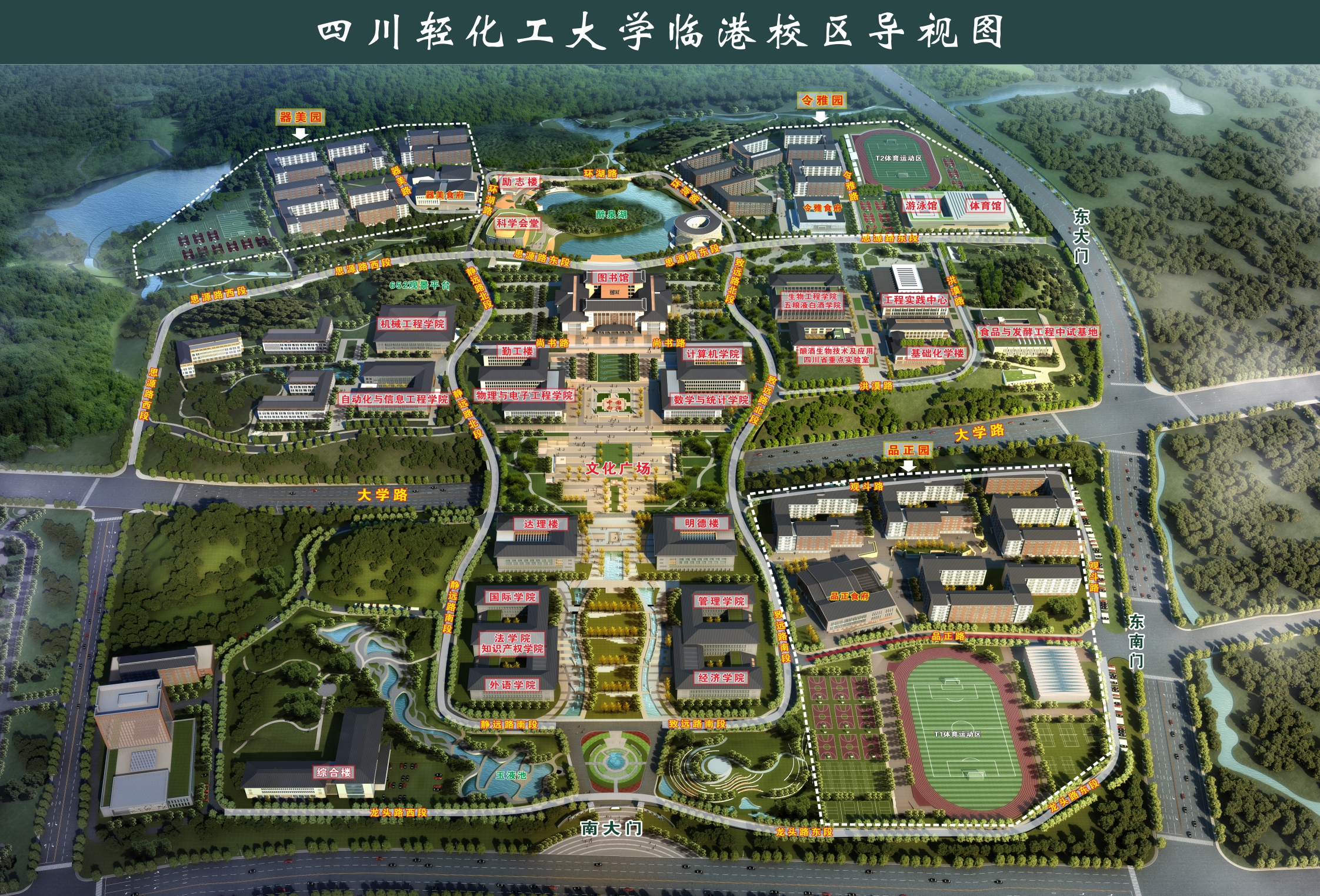
二、实验代码
#include<stdio.h>
#include<conio.h>
#include<iostream>
#include<assert.h>
#include<string.h>
#include<fstream>
#include <vector>
#define INF 123456
#define MaxSize 32476
using namespace std;
typedef struct
char name[100];
char info[10000];
VertexType; //顶点结构[name+info]
typedef struct
VertexType vexs[10];
int arcs[100][100]; //邻接矩阵
int vexnum,arcnum; //顶点、边的个数
MGraph;
//确定边的位置
int locatevex(MGraph &G,char v[],int vexnum)
for(int i=0;i<vexnum;i++)
if(v==G.vexs[i].name)
return i;
//输出所有景点的名称
void show_vex(MGraph &G)
for(int i=0;i<G.vexnum;i++)
cout<<i+1<<"."<<G.vexs[i].name<<endl;
//输出所有景点的详细信息
void show_info(MGraph &G,int index)
cout<<"对应景点信息为:"<<index<<"."<<G.vexs[index-1].info<<endl;
//获取编号
int getVerNum(MGraph &G,char* name)
int i;
for(i=0;i<G.vexnum;i++)
if(strcmp(name,G.vexs[i].name)==0)
return i;
if(i>G.vexnum)
return -1;
// 最短路径Dijkstra算法
/*
v: 求编号为v的顶点到其它点的最短路径。
path: 路径存放在path数组中。 path[i] 存放 到i的前驱结点编号, path[3] = 1 表示: 顶点3是从1过来的
*/
void Dijkstra(MGraph &G,int v,int path[],int dist[])
int s[MaxSize];// 已找到最短路径的点的集合
bool Final[MaxSize];//Final[w]=1表示求得顶点V0至Vw的最短路径
// 初始化dist\\path: path[i] 存放 到i的前驱结点编号, -1表示没有
for (int i = 0; i < G.vexnum; i++)
Final[i] = false;
dist[i] = G.arcs[v][i];
if (dist[i] != INF)
path[i] = v;
else
path[i]=-1;
s[0] = v; // 初始化s
Final[v] = true;
int num = 1;
while (num < G.vexnum)
// 在dist中查找最小值元素
int k = 0,min= INF;
for (int i = 0; i < G.vexnum; i++)
if (i == v)continue;
if (!Final[i] && dist[i] < min)
k = i;
min = dist[i];
s[num++] = k;// 将新生成的结点加入集合s
Final[k] = true;
// 修改dist和path数组
for (int i = 0; i < G.vexnum; i++)
if (!Final[i] && dist[i] > dist[k] + G.arcs[k][i])
dist[i] = dist[k] + G.arcs[k][i];
path[i] = k;
/* char*tostr 字符串转化str类型
输入:char * 字符串地址
无输出
返回值: str类型的字符串
*/
string charToStr(char * contentChar)
string str;
for (int i=0;contentChar[i]!='\\0';i++)
str+=contentChar[i];
return str;
/* 修改文件某行内容
输入:文件名 fileName 行号 lineNum ,修改的内容 content
输出:文件名 fileName
无返回值
tip:1,lineNum从第一行开始 2.content需要加上换行符
*/
void modifyContentInFile(char *fileName,int lineNum,char *content)
ifstream in;
char line[1024]='\\0';
in.open(fileName);
int i=0;
string tempStr;
while(in.getline(line,sizeof(line)))
i++;
if(lineNum!=i)
tempStr+=charToStr(line);
else
tempStr+=charToStr(content);
tempStr+='\\n';
in.close();
ofstream out;
out.open(fileName);
out.flush();
out<<tempStr;
out.close();
void CreatGraph(MGraph &G)
ifstream in("Graph.txt");
in>>G.vexnum>>G.arcnum;
for(int i=0;i<G.vexnum;i++)
in>>G.vexs[i].name;
in>>G.vexs[i].info;
//输出
//初始化边的权值
for(int i=0;i<G.vexnum;i++)
for(int j=0;j<G.vexnum;j++)
G.arcs[i][j]=INF;
//输入边的信息
for(int i=0;i<G.arcnum;i++)
int m,n,cost;
char tname1[MaxSize],tname2[MaxSize];
in>>tname1>>tname2>>cost;
m=getVerNum(G,tname1);
n=getVerNum(G,tname2);
//如果m n为-1,表示输入有错
assert(m!=-1&&n!=-1);
G.arcs[m][n]=cost;
G.arcs[n][m]=cost;
/*删除文本文件的空行*/
void deletenull(string file)
vector<string> file_data;
string file_name = file;
fstream file_in(file_name.c_str(), fstream::in);
string temp = "";
while( getline(file_in, temp) )
if( temp != "")
file_data.push_back(temp);
file_in.close();
//remove(file_name.c_str());
fstream file_out(file_name.c_str(), fstream::out);
for(vector<string>::iterator i = file_data.begin(); i != file_data.end(); i++)
file_out<<*i<<endl;
int main()
while(1)
cout<<"***************欢迎来到四川轻化工大学********"<<endl;
cout<<"1. 查询景点信息"<<endl;
cout<<"2. 问路查询"<<endl;
cout<<"3. 修改一个已有景点的相关信息;"<<endl;
cout<<"4. 增加一个新景点及其相关信息"<<endl;
cout<<"5. 增加一条新的路径"<<endl;
cout<<"6. 删除一个景点及其相关信息"<<endl;
cout<<"7. 删除一条路径"<<endl;
cout<<"#. 退出"<<endl;
cout<<"***************轻化工校园导游系统**********"<<endl;
MGraph G;
CreatGraph(G); //首先创建图
char ch;
cout<<"请输入:";cin>>ch;
if(ch=='#')
break;
else if(ch=='1')
cout<<"本校景点有:"<<endl;
show_vex(G);
cout<<"-------------"<<endl;
cout<<"请选择您要查询的景点:"<<"(1-"<<G.vexnum<<")"<<"[注:输入0就退出该功能]"<<endl;
int index;
while(1)
cin>>index;
if(index==0) break;
if(index>=1&&index<=G.vexnum)
show_info(G,index);
else
cout<<"Search failed!"<<endl;
else if(ch=='2')
cout<<"你选择了问路查询!"<<endl<<"下面显示景点列表:"<<endl;
show_vex(G);
cout<<"-------------"<<endl;
int from,end;
cout<<"请输入你现在的位置:"<<endl;
while(1)
cin>>from;
if(from<=0||from>G.vexnum)
cout<<"Input failed!Please input the start again:"<<endl;
else
break;
cout<<"请输入你的目的地:"<<endl;
while(1)
cin>>end;
if(end<=0||end>G.vexnum)
cout<<"Input failed!Please input the end again:"<<endl;
else
break;
int path[MaxSize];
int dist[MaxSize]; //v到j的路径长度
Dijkstra(G,from-1,path,dist);
cout<<G.vexs[from-1].name<<"到"<<G.vexs[end-1].name<<"的路径是:"<<endl;
int temp=end-1; //终点-1作为数组下标
int temp1,temp2;
int flag[MaxSize],m=0;
while(temp!= -1 )
flag[m++]=temp; //flag[]用来
temp1=temp;
temp2=path[temp1]; //path[]存放前驱顶点编号。path[temp1]=-1表示没有前驱了。
temp=temp2;
for(int i=m-1;i>=0;i--)
cout<<G.vexs[ flag[i] ].name;
if(i!=0)
cout<<"->";
cout<<endl<<endl;
cout<<"最短距离是:"<<endl<< dist[end-1] <<"米"<<endl; //dist[]数组用来存放出发节点v0到每个节点的最短路径; dist[end-1]表示v0到终点的最短路径
cout<<"---------------------------------"<<endl;
else if(ch=='3')
char file[10]="graph.txt";
cout<<"输入需要修改信息的原景点:"<<endl;
int i;cin>>i;
cout<<"将原景点信息改为:---->"<<endl;
char content[1000]="",s[100];
cin>>s;
strcat(content,G.vexs[i-1].name); strcat(content," "); strcat(content,s);
//cout<<content<<endl;
modifyContentInFile(file,1+i,content);cout<<"修改景点信息成功!"<<endl;
else if(ch=='4')
//增加一个新景点及其相关信息
cout<<"你选择了增加一个新景点及其相关信息功能!"<<endl;
cout<<"请输入新景点的name和info:"<<endl;
char newvexname[MaxSize];char newvexinfo[MaxSize];
cin>>newvexname;cin>>newvexinfo;
strcat(newvexname," ");strcat(newvexname,newvexinfo);
char s[MaxSize];
strcpy(s,G.vexs[G.vexnum-1].name);
strcat(s," ");
strcat(s,G.vexs[G.vexnum-1].info);
strcat(s,"\\n");strcat(s,newvexname);
cout<<s<<endl;
//插入到景点末尾;而且将第一行的vexnum+1;
char file[10]="graph.txt";
modifyContentInFile(file,1+G.vexnum,s);
char str1[MaxSize];char str2[MaxSize];
itoa(G.vexnum+1, str1, 10); //第三个参数表示多少进制
itoa(G.arcnum,str2,10);
strcat(str1," ");strcat(str1,str2);
modifyContentInFile(file,1,str1); //修改第一行
else if(ch=='5')
//增加一条新的路径;
cout<<"你选择了增加一条新的路径!"<<endl<<"请依次输入新路径的起点和终点和路径长度:"<<endl;
char s1[MaxSize];char s2[MaxSize];char s3[MaxSize];
cin>>s1>>s2>>s3;
strcat(s1," ");strcat(s1,s2);strcat(s1," ");strcat(s1,s3);
//在文件末尾写入
ofstream write;
ifstream read;
write.open("graph.txt", ios::app); //用ios::app不会覆盖文件内容
write << s1 << endl;
write.close();
read.close();
//下面把8 15改成8 16,需要将arcnum++,然后第一行转化成字符串,再写入
char str1[MaxSize];char str2[MaxSize];
itoa(G.vexnum, str1, 10); //第三个参数表示多少进制
itoa(G.arcnum+1,str2,10);
strcat(str1," ");strcat(str1,str2);
//修改第一行
char file[10]="graph.txt";
modifyContentInFile(file,1,str1);
else if(ch=='6')
//删除一个景点及其相关信息;
cout<<"你选择了删除一个景点及其相关信息!" <<endl<<"请输入你要删除的景点编号:"<<endl;
int i;
cin>>i;
char file[10]="graph.txt";
modifyContentInFile(file,1+i,"");
char str1[MaxSize];char str2[MaxSize];//修改第一行
itoa(G.vexnum-1, str1, 10);
itoa(G.arcnum,str2,10);
strcat(str1," ");strcat(str1,str2);
modifyContentInFile(file,1,str1);
string file1="graph.txt";
deletenull(file1);
else if(ch=='7')
//删除一条路径
cout<<"你选择了删除一条路径功能!"<<endl;
ifstream in("graph.txt");
string str;
string temp;
for(int i=0;i<1+G.vexnum;i++)
getline(in,temp);
cout<<"以下展示出所有路径:"<<endl;
for(int i=0;i<G.arcnum;i++)
getline(in,str);
cout<<i+1<<"."<<str<<endl;
cout<<"请输入删除的路径(1-"<<G.arcnum<<"):"<<endl;
int index; cin>>index;
char file[10]="graph.txt";
modifyContentInFile(file,1+G.vexnum+index,""); //删除路径
char str1[MaxSize];char str2[MaxSize];
itoa(G.vexnum, str1, 10);
itoa(G.arcnum-1,str2,10);
strcat(str1," ");strcat(str1,str2);
modifyContentInFile(file,1,str1); //修改第一行
string file1="graph.txt";
deletenull(file1);
else
//如果输入不为1-7和#的话
cout<<"------------------"<<endl<<"Input failed!Please input again!"<<endl<<"------------------"<<endl;
return 0;
三、编译后运行截图:
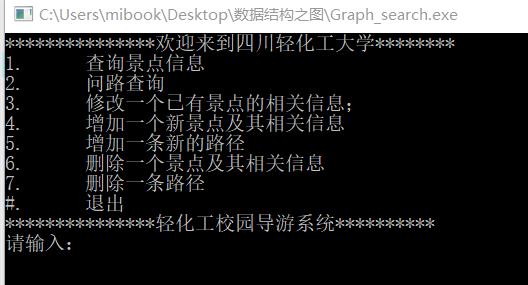
四、附上数据文件“graph.txt”中的内容(用于测试):

五、注:
在对“图”中的数据进行增、删、改、查,实验要求对文件进行处理。
除了基本的方法以外,另外其中有几个函数或算法可以深入思考、学习:
1.删除文件中的空白行:
void deletenull(string file)
vector<string> file_data;
string file_name = "1.txt";
fstream file_in(file_name.c_str(), fstream::in);
string temp = "";
while(getline(file_in, temp))
if( temp != "")
file_data.push_back(temp);
file_in.close();
//remove(file_name.c_str());
fstream file_out(file_name.c_str(), fstream::out);
for(vector<string>::iterator i = file_data.begin(); i != file_data.end(); i++)
file_out<<*i<<endl;
2.修改文件中指定行的内容
/* 修改文件某行内容
输入:文件名 fileName 行号 lineNum ,修改的内容 content
输出:文件名 fileName
无返回值
tip:1,lineNum从第一行开始 2.content需要加上换行符
*/
void modifyContentInFile(char *fileName,int lineNum,char *content)
ifstream in;
char line[1024]='\\0';
in.open(fileName);
int i=0;
string tempStr;
while(in.getline(line,sizeof(line)))
i++;
if(lineNum!=i)
tempStr+=charToStr(line);
else
tempStr+=charToStr(content);
tempStr+='\\n';
in.close();
ofstream out;
out.open(fileName);
out.flush();
out<<tempStr;
out.close();
字符串*char类型转为字符串string类型
/* char*tostr 字符串转化str类型
输入:char * 字符串地址
无输出
返回值: str类型的字符串
*/
string charToStr(char * contentChar)
string str;
for (int i=0;contentChar[i]!='\\0';i++)
str+=contentChar[i];
return str;
3.最短路径算法(这里是Dijkstra算法,另外可参考Floyd算法):
// 最短路径Dijkstra算法
/*
v: 求编号为v的顶点到其它点的最短路径。
path: 路径存放在path数组中。 path[i] 存放 到i的前驱结点编号, path[3] = 1 表示: 顶点3是从1过来的
*/
void Dijkstra(MGraph &G,int v,int path[],int dist[])
int s[MaxSize];// 已找到最短路径的点的集合
bool Final[MaxSize];//Final[w]=1表示求得顶点V0至Vw的最短路径
// 初始化dist\\path: path[i] 存放 到i的前驱结点编号, -1表示没有
for (int i = 0; i < G.vexnum; i++)
Final[i] = false;
dist[i] = G.arcs[v][i];
if (dist[i] != INF)
path[i] = v;
else
path[i]=-1;
s[0] = v; // 初始化s
Final[v] = true;
int num = 1;
while (num < G.vexnum)
// 在dist中查找最小值元素
int k = 0,min= INF;
for (int i = 0; i < G.vexnum; i++)
if (i == v)continue;
if (!Final[i] && dist[i] < min)
k = i;
min = dist[i];
s[num++] = k;// 将新生成的结点加入集合s
Final[k] = true;
// 修改dist和path数组
for (int i = 0; i < G.vexnum; i++)
if (!Final[i] && dist[i] > dist[k] + G.arcs[k][i])
dist[i] = dist[k] + G.arcs[k][i];
path[i] = k;
以上是关于图的应用(校园导航图最短路径求解)的主要内容,如果未能解决你的问题,请参考以下文章