数字图像处理学习笔记（十四）——频域图像增强（图像的频域分析）
Posted 闭关修炼——暂退
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数字图像处理学习笔记（十四）——频域图像增强（图像的频域分析）相关的知识，希望对你有一定的参考价值。
数字图像处理(Digital Image Processing)是通过计算机对图像进行去除噪声、增强、复原、分割、提取特征等处理的方法和技术。本专栏将以学习笔记形式对数字图像处理的重点基础知识进行总结整理，欢迎大家一起学习交流！
专栏链接：数字图像处理学习笔记
目录
1 频率域平滑（低通）滤波器
图像的平滑除了在空间域中进行外，也可以在频率域中进行。
由于噪声主要集中在高频部分，为去除噪声改善图像质量，滤波器采用低通滤波器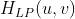
来抑制高频成分，通过低频成分，然后再进行逆傅立叶变换获得滤波图像，就可达到平滑图像的目的。
边缘和噪声等尖锐变化处于傅里叶变换的高频部分
平滑可以通过衰减高频成分的范围来实现
常用的频率域平滑滤波器有3种:
- 理想低通滤波器 （处理变化尖锐部分）
- 巴特沃思低通滤波器 （处于理想和高斯滤波器之间）
- 高斯低通滤波器 （处理变化平滑部分）
1.1 理想低通滤波器
高度概括：截断傅里叶变换中的所有处于指定距离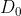
之外的高频成分。
简单而言：就是将以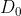为半径的圆以外的部分全部置0，远行以内的部分全部置1。
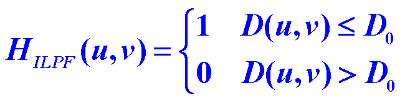
上述公式即为理想低通滤波器的公式描述。
其中，H代表滤波器，I代表理想，LP代表低通，F代表滤波器。
因为该公式是在频域中的，故用u,v表示；而x,y是空间域常用的表示形式。
★低通滤波器随着半径的增大保留的信息增多
频率域的中心在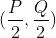
，从点
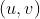到中心（原点）的距离如下
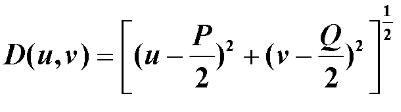
图像描述
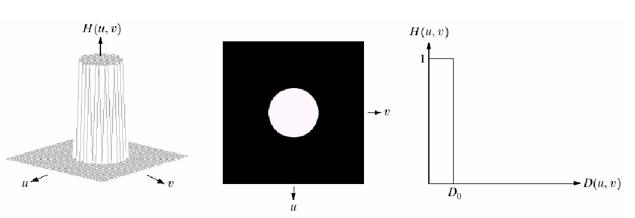
说明：在半径为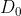的圆内，所有频率没有衰减地通过滤波器，而在此半径的圆之外的所有频率完全被衰减掉。
总图像功率值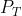
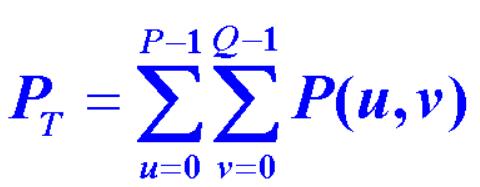
其中:
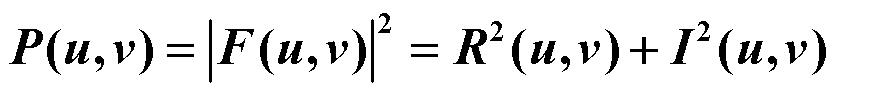
原点在频率域的中心，半径为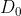的圆包含
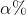的功率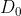
其中
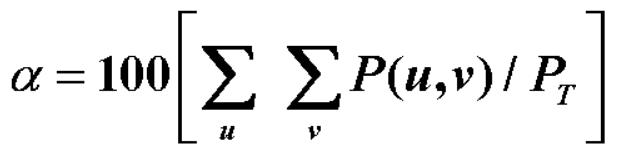
理想低通滤波器举例
上图所示的是：
圆环具有半径5,15,30,80和230个像素
图像功率为92.0%,94.6%,96.4%,98.0%和99.5%
此举例说明结论:
①90%以上的功率(能量)集中在半径小于5的圆周内;
②随滤波器半径的增加,越来越少的功率被滤出掉,使模糊减弱。
理想低通滤波器具有振铃现象
1.2 巴特沃思低通滤波器
n阶巴特沃思低通滤波器(BLPF)定义如下
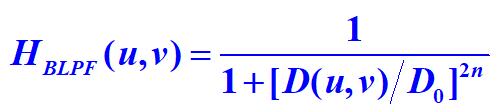
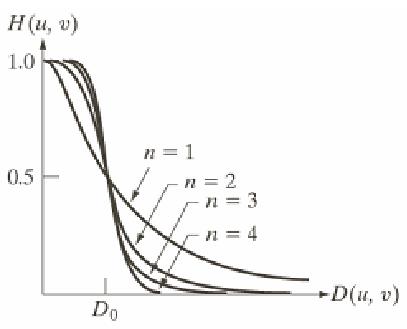
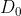为截至频率距原点的距离，D(u,v)是点(u,v)距原点的距离。
当D(u,v)=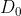时，H(u,v)=0.5(最大值是1，当D(u,v)=0)
它的特性是连续性衰减，而不像理想滤波器那样陡峭变化， 即明显的不连续性。
因此采用该滤波器滤波在抑制噪声的同时，图像边缘的模糊程度大大减小，没有振铃效应产生。
图像描述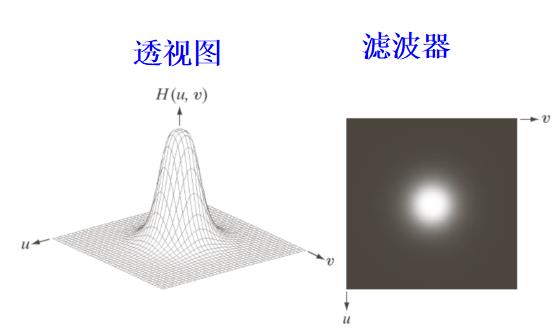
可用于平滑处理，如图像由于量化不足产生虚假轮廓时，常可用低通滤波进行平滑以改进图像质量。
通常，BLPF的平滑效果好于ILPF（振铃现象）。
巴特沃思低通滤波器 n=2（n=2时效果最好）
所有的滤波器都有半径为5的截至频率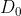
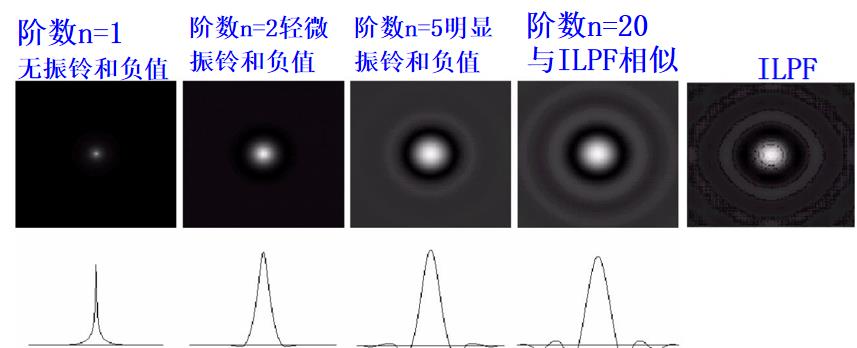
注：二阶BLPF处于有效低通滤波和可接受的振铃特征之间。
1.3 高斯低通滤波器
二维高斯低通滤波器(GLPF)定义如下
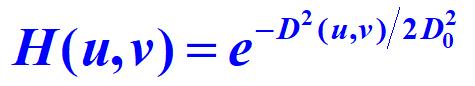
当D(u,v)=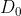时，滤波器下降到它最大值的0.607处
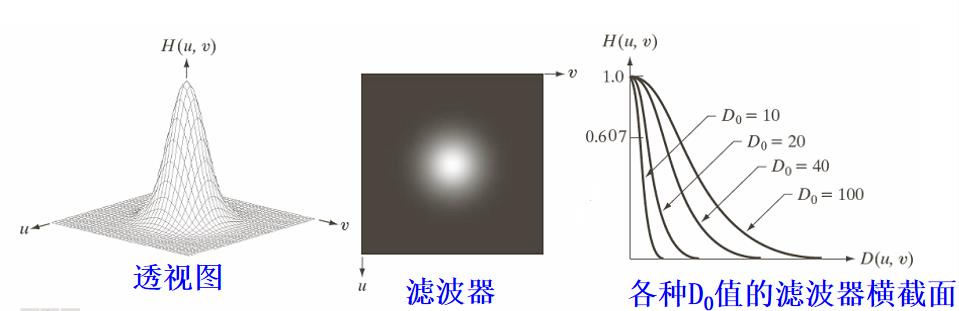
图像描述
采用高斯低通滤波器滤波在抑制噪声的同时，图像边缘的模糊程度较用Butterworth滤波产生的大些，无明显的振铃效应。
★高斯滤波器无振铃现象
1.4 三种低通滤波器小结
GLPF不能达到有相同截止频率的二阶BLPF的平滑效果
GLPF没有振铃
如果需要严格控制低频和高频之间截至频率的过渡，选用BLPF，代价是可能产生振铃
1.5 低通滤波器的应用实例：模糊,平滑等
字符识别：通过模糊图像，桥接断裂字符的裂缝
印刷和出版业：从一幅尖锐的原始图像产生平滑、柔和的外观，如人脸，减少皮肤细纹的锐化程度和小斑点
处理卫星和航空图像：尽可能模糊细节，而保留大的可识别特征。低通滤波通过消除不重要的特征来简化感兴趣特征的分析
2 频率域锐化（高通）滤波器
图像的边缘、细节主要位于高频部分，而图像的模糊是由于高频成分比较弱产生的。
频率域锐化就是为了消除模糊，突出边缘。
因此采用高通滤波器让高频成分通过，使低频成分削弱，再经逆傅立叶变换得到边缘锐化的图像
频率域锐化滤波器主要有：
- 理想高通滤波器
- 巴特沃思高通滤波器
- 高斯高通滤波器
- 频率域的拉普拉斯算子
- 钝化模板、高频提升滤波和高频加强滤波
高通滤波器的频域表示：
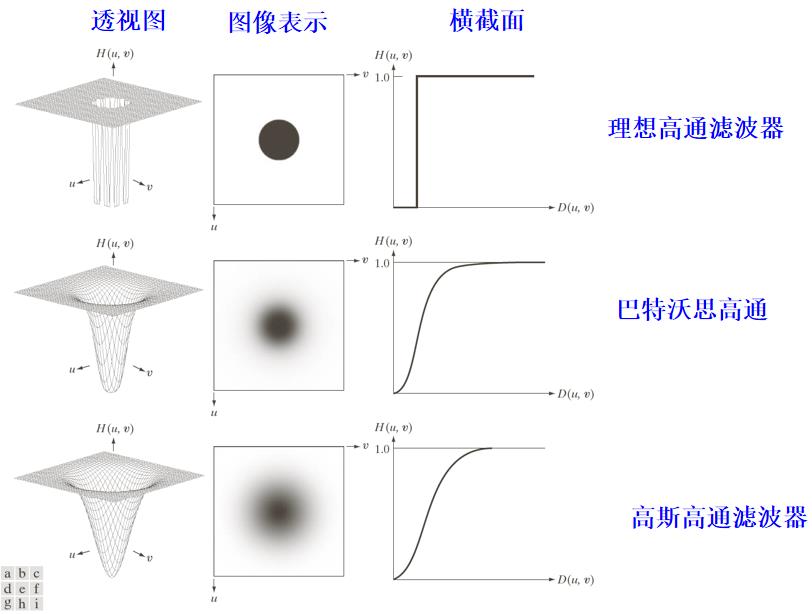
巴特沃思滤波器为理想滤波器的尖锐化和高斯滤波器的完全光滑之间的一种过渡。
高通滤波器的空间域表示：
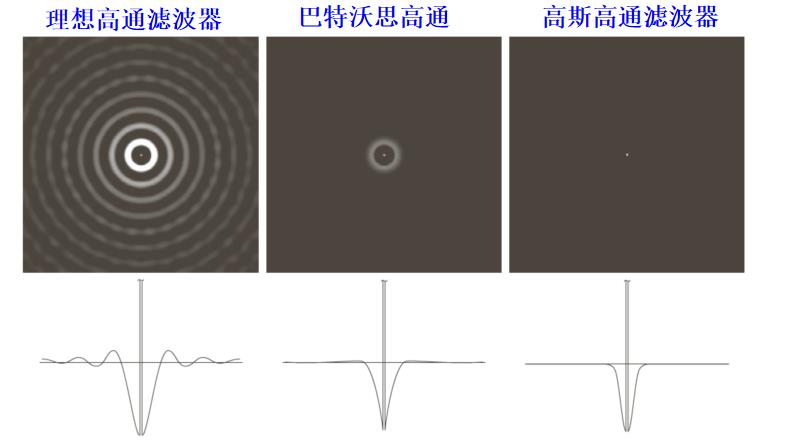
2.1 理想高通滤波器（IHPF）
截断傅里叶变换中所有处于指定距离D0之内的低频成分
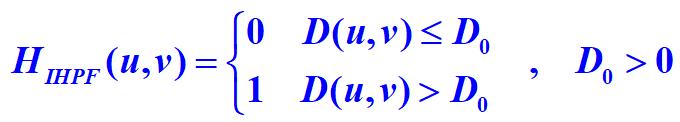
频率域的中心在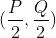，从点(u,v)到中心（原点）的距离如下
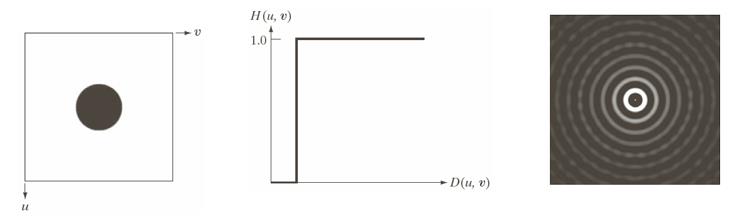
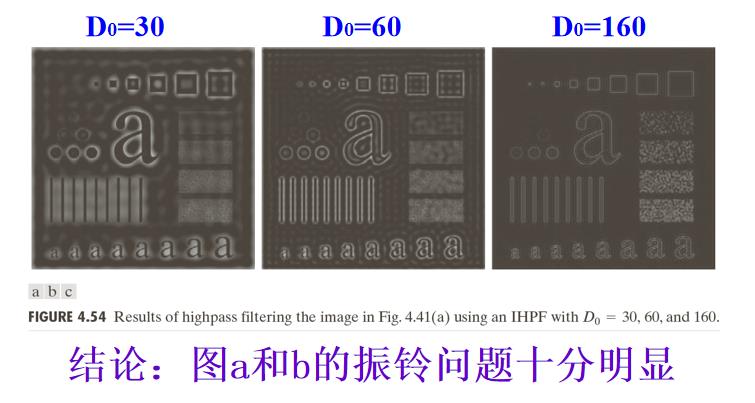
理想高通滤波示例：
2.2 巴特沃思高通滤波器
n阶巴特沃思高通滤波器(BHPF)定义如下
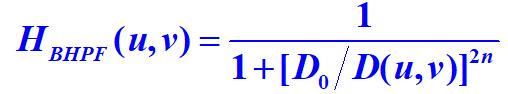
推导
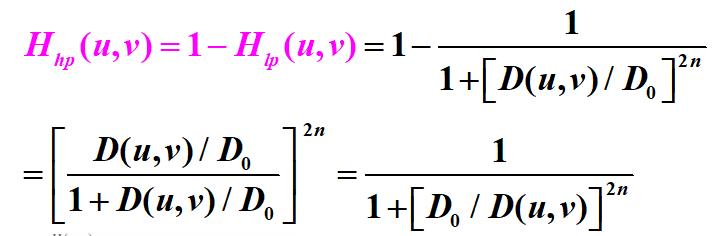
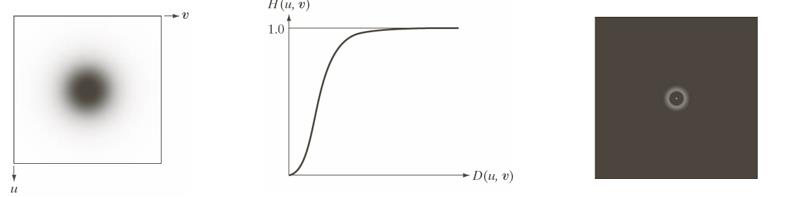
二阶巴特沃思高通滤波示例：
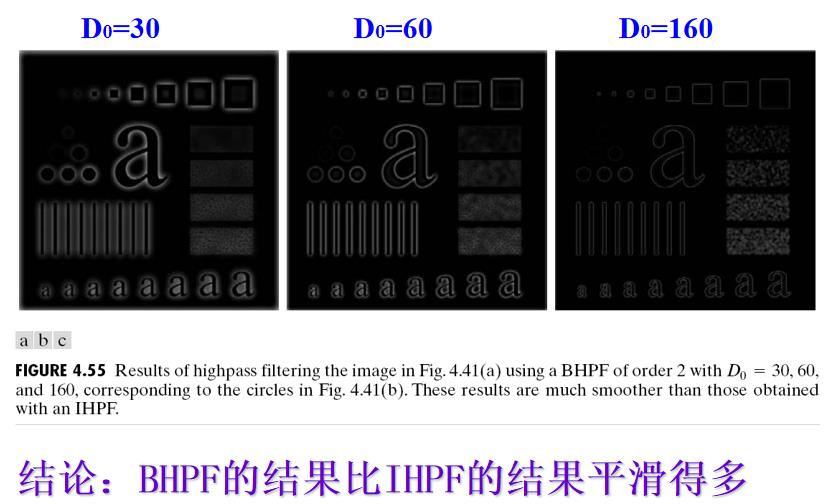
2.3 高斯（指数）高通滤波器
截频距原点为D0的高斯高通滤波器(GHPF)定义为
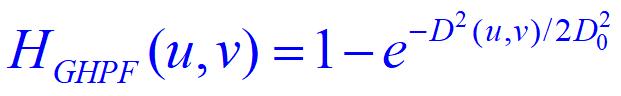
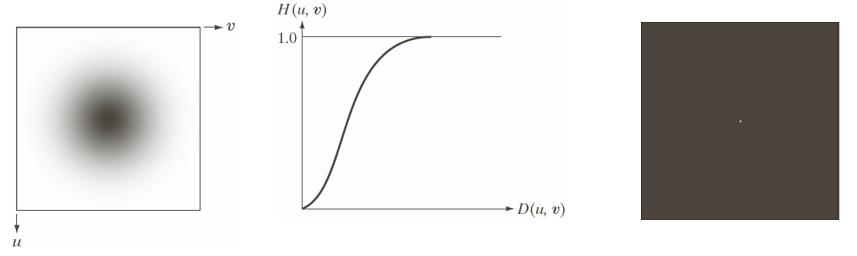
高斯高通滤波示例：
2.4 三种高通滤波器小结
三种滤波函数的选用类似于低通。
理想高通有明显振铃现象，即图像的边缘有抖动现象；
Butterworth高通滤波效果较好，但计算复杂，其优点是有少量低频通过，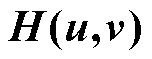
是渐变的，振铃现象不明显；
指数高通效果比Butterworth差些，振铃现象不明显；
一般来说，不管在图像空间域还是频率域，采用高频滤波不但会使有用的信息增强，同时也使噪声增强。因此不能随意地使用
2.5 频率域的拉普拉斯算子
频率域的拉普拉斯算子定义
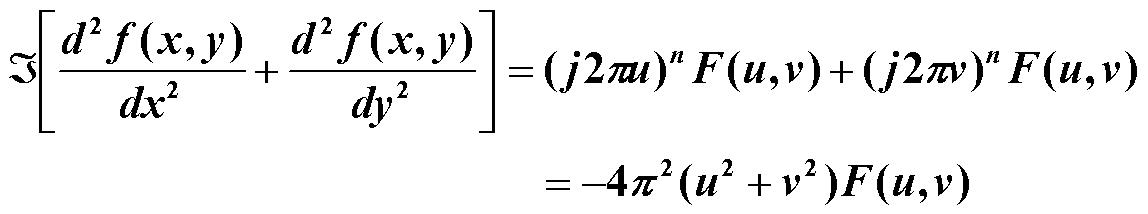
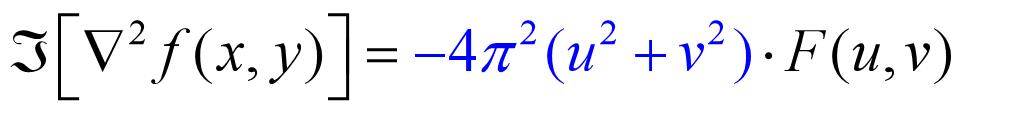
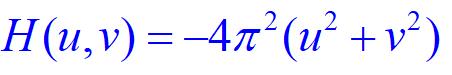
原点从(0,0)移到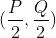,所以，滤波函数平移为
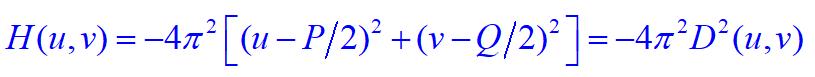
空间域拉普拉斯算子过滤后的图像可由计算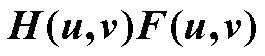
的反傅里叶变换得到
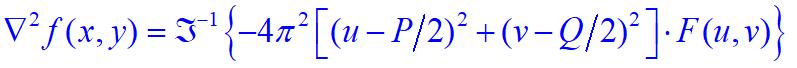
傅里叶变换对表示空间域拉普拉斯算子和频率域的双向关系
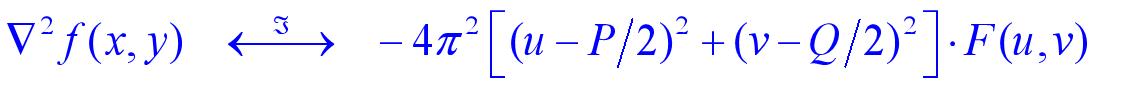
从原始图像中减去拉普拉斯算子部分，形成g(x,y)的增强图像
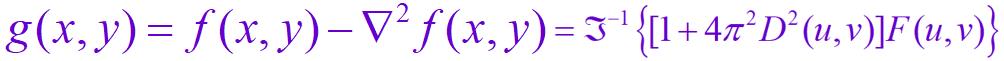
2.6 钝化模板、高频提升滤波和高频加强滤波
为什么要进行高频提升和高频加强？
高频滤波后的图像，其背景平均强度减小到接近黑色（因为高通滤波器滤除了傅里叶变换的零频率成分:F(0,0)=0）
解决办法：把原始图像加到过滤后的结果中，如拉普拉斯算子增强，这种处理称为高频提升过滤。它是钝化模板的推广。
钝化模板(锐化或高通图像)：
从一幅图像减去其自身模糊图像从而生成锐化图像。
在频率域，即从图像本身减去低通滤波（模糊）后的图像而得到高通滤波（锐化）的图像。
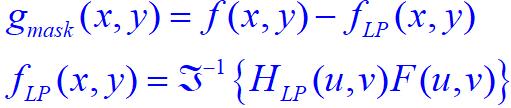
钝化模板和高频提升过滤：
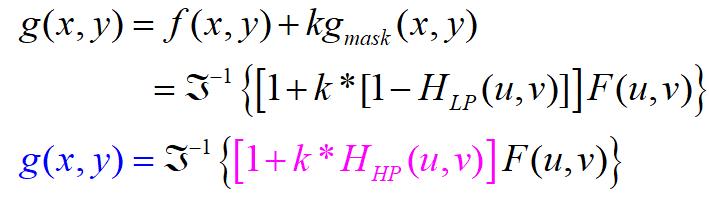
当k=1,即钝化模板；当k>1,高提升滤波。
更一般的高频提升加强：
用图像的高频成分进行增强
增加k1的目的是使零频率不被滤波器过滤
当k2>1，高频得到加强
欢迎留言，一起学习交流~~~
感谢阅读
END
以上是关于数字图像处理学习笔记（十四）——频域图像增强（图像的频域分析）的主要内容，如果未能解决你的问题，请参考以下文章