机器学习-白板推导系列笔记（十九）-贝叶斯线性回归
Posted 及时行樂_
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习-白板推导系列笔记（十九）-贝叶斯线性回归相关的知识，希望对你有一定的参考价值。
此文章主要是结合哔站shuhuai008大佬的白板推导视频：贝叶斯线性回归_81min
全部笔记的汇总贴：机器学习-白板推导系列笔记
一、背景介绍
我们首先回顾一下线性回归，线性回归是最简单的回归问题。
D a t a : ( x i , y i ) i = 1 N , x i ∈ R p , y i ∈ R Data:\\(x_i,y_i)\\^N_i=1,x_i\\in R^p,y_i\\in R Data:(xi,yi)i=1N,xi∈Rp,yi∈R
X = ( x 1 x 2 ⋯ x N ) T = ( x 1 T x 2 T ⋮ x N T ) = ( x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋮ ⋮ ⋮ x N 1 x N 2 ⋯ x N p ) X=(x_1\\;x_2\\;\\cdots\\;x_N)^T=\\left(\\beginmatrixx_1^T \\\\ x_2^T \\\\\\vdots\\\\x_N^T\\endmatrix\\right)=\\left(\\beginmatrixx_11\\;x_12\\;\\cdots\\;x_1p \\\\x_21\\;x_22\\;\\cdots\\;x_2p \\\\\\vdots\\;\\;\\;\\;\\vdots\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;\\vdots \\\\x_N1\\;x_N2\\;\\cdots\\;x_Np \\endmatrix\\right) X=(x1x2⋯xN)T=⎝⎜⎜⎜⎛x1Tx2T⋮xNT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x12⋯x1px21x22⋯x2p⋮⋮⋮xN1xN2⋯xNp⎠⎟⎟⎟⎞
Y = ( y 1 y 2 ⋮ y N ) N ∗ 1 Y=\\left(\\beginmatrixy_1 \\\\ y_2 \\\\\\vdots\\\\y_N\\endmatrix\\right)_N*1 Y=⎝⎜⎜⎜⎛y1y2⋮yN⎠⎟⎟⎟⎞N∗1
所以线性回归模型为： f ( x ) = W T x = x T W y = f ( x ) + ε ( n o i s e ) f(x)=W^Tx=x^TW\\\\y = f(x)+\\varepsilon(noise) f(x)=WTx=xTWy=f(x)+ε(noise)
其中， x , y , ε a r e r . v x ∈ R p , y ∈ R , ε ∼ N ( 0 , σ 2 ) x,y,\\varepsilon \\;\\;are\\;\\;r.v\\\\x\\in R^p,y\\in R,\\varepsilon\\sim N(0,\\sigma^2) x,y,εarer.vx∈Rp,y∈R,ε∼N(0,σ2)
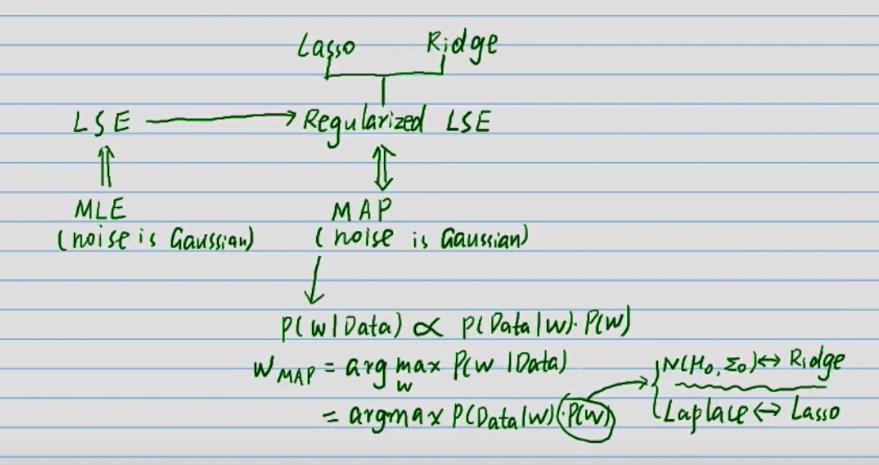
频率派（w is unknown constant）是一个优化问题，点估计。
MLE中有，
W
M
L
E
=
arg max
w
p
(
D
a
t
a
∣
w
)
W_MLE=\\undersetw\\argmaxp(Data|w )
WMLE=wargmaxp(Data∣w)
MAP中有（上图所示），
W
M
A
P
=
arg max
w
p
(
D
a
t
a
∣
w
)
W_MAP=\\undersetw\\argmaxp(Data|w )
WMAP=wargmaxp(Data∣w)
而现在主要使用贝叶斯方法，属于贝叶斯派（w is r.v），不属于点估计也不是优化问题，而是要把后验 p ( w ∣ D a t a ) p(w|Data) p(w∣Data)求出来。
二、推导
（一）介绍
还是先给数据，
D a t a : ( x i , y i ) i = 1 N , x i ∈ R p , y i ∈ R Data:\\(x_i,y_i)\\^N_i=1,x_i\\in R^p,y_i\\in R Data:(xi,yi)i=1N,xi∈Rp,yi∈R
X = (以上是关于机器学习-白板推导系列笔记（十九）-贝叶斯线性回归的主要内容，如果未能解决你的问题，请参考以下文章
机器学习线性回归——岭回归从贝叶斯角度理解（理论+图解+公式推导）