中科大-凸优化 笔记(lec3)-仿射集
Posted 及时行樂_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了中科大-凸优化 笔记(lec3)-仿射集相关的知识,希望对你有一定的参考价值。
全部笔记的汇总贴(视频也有传送门):中科大-凸优化
过任意两点的直线:
y
=
θ
x
1
+
(
1
−
θ
)
x
2
,
θ
∈
R
y=\\theta x_1+(1-\\theta)x_2,\\theta\\in\\R
y=θx1+(1−θ)x2,θ∈R
任意两点间的线段:
y
=
θ
x
1
+
(
1
−
θ
)
x
2
,
θ
∈
[
0
,
1
]
y=\\theta x_1+(1-\\theta)x_2,\\theta\\in[0,1]
y=θx1+(1−θ)x2,θ∈[0,1]
一、仿射集(Affine Sets)
x 1 ≠ x 2 ∈ R n , θ ∈ R ⟹ y = θ x 1 + ( 1 − θ ) x 2 = x 2 + θ ( x 1 − x 2 ) 直 线 x_1\\neq x_2\\in\\R^n,\\theta\\in\\R\\Longrightarrow y=\\theta x_1+(1-\\theta)x_2=x_2+\\theta(x_1-x_2)\\;\\;直线 x1=x2∈Rn,θ∈R⟹y=θx1+(1−θ)x2=x2+θ(x1−x2)直线
x 1 ≠ x 2 ∈ R n , θ ∈ [ 0 , 1 ] ⟹ y = θ x 1 + ( 1 − θ ) x 2 线 段 x_1\\neq x_2\\in\\R^n,\\theta\\in [0,1]\\Longrightarrow y=\\theta x_1+(1-\\theta)x_2\\;\\;线段 x1=x2∈Rn,θ∈[0,1]⟹y=θx1+(1−θ)x2线段
仿射集:一个集合
C
C
C是仿射集,若
∀
x
1
,
x
2
∈
C
\\forall x_1,x_2\\in C
∀x1,x2∈C,则连接
x
1
x_1
x1和
x
2
x_2
x2的直线也在集合内。
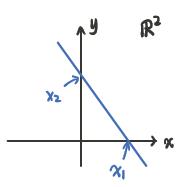
直线、 R 2 \\R^2 R2是仿射集;线段、闭合图形不是仿射集。
设 k k k个点 x 1 , ⋯ , x k ∈ C , θ 1 , ⋯ , θ k ∈ R , θ + ⋯ + θ k = 1 x_1,\\cdots,x_k\\in C,\\theta_1,\\cdots,\\theta_k\\in\\R,\\theta+\\cdots+\\theta_k=1 x1,⋯,xk∈C,θ1,⋯,θk∈R,θ+⋯+θk=1
仿射组合: θ 1 x 1 + ⋯ + θ k x k ( 一 个 点 ) θ 1 x 1 + ⋯ + θ k x k ∈ C ⇔ C 是 仿 射 集 \\theta_1x_1+\\cdots+\\theta_kx_k(一个点)\\\\\\theta_1x_1+\\cdots+\\theta_kx_k\\in C\\Leftrightarrow C是仿射集 θ1x1+⋯+θkxk(一个点)θ1x1+⋯+θkxk∈C⇔C是仿射集
有仿射集 C C C, x 1 , x 2 , x 3 ∈ C , θ 1 , θ 2 , θ 3 ∈ R , θ 1 + θ 2 + θ 3 = 1 x_1,x_2,x_3\\in C,\\theta_1,\\theta_2,\\theta_3\\in\\R,\\theta_1+\\theta_2+\\theta_3=1 x1,x2,x3∈C,θ1,θ2,θ3∈R,θ1+θ2+θ3=1
θ 1 θ 1 + θ 2 x 1 + θ 2 θ 1 + θ 2 x 2 ∈ C ( θ 1 + θ 2 ) ( θ 1 θ 1 + θ 2 x 1 + θ 2 θ 1 + θ 2 x 2 ) + ( 1 − θ 1 − θ 2 ) x 3 ∈ C θ 1 x 1 + θ 2 x 2 + θ 3 x 3 ∈ C \\frac\\theta_1\\theta_1+\\theta_2x_1+\\frac\\theta_2\\theta_1+\\theta_2x_2\\in C\\\\(\\theta_1+\\theta_2)\\Big(\\frac\\theta_1\\theta_1+\\theta_2x_1+\\frac\\theta_2\\theta_1+\\theta_2x_2\\Big)+(1-\\theta_1-\\theta_2)x_3\\in C\\\\\\;\\\\\\theta_1x_1+\\theta_2x_2+\\theta_3x_3\\in C θ1+θ2θ1x1+θ1+以上是关于中科大-凸优化 笔记(lec3)-仿射集的主要内容,如果未能解决你的问题,请参考以下文章