邓俊辉 《数据结构》笔记1 绪论

Posted 2022-12-21 临风而眠

邓俊辉 《数据结构》笔记1 绪论

CSDN转图床总是崩，如果全写完再上传一次要调好多，感觉很麻烦，所以写一点更新一点，会持续更新

提前发出来还有个好处就是push自己更新不会咕咕咕，哈哈

参考资料

• MOOC 数据结构上
• MOOC 数据结构下
• 大佬笔记1
• 大佬笔记2

文章目录

• 邓俊辉 《数据结构》笔记1 绪论
• 参考资料
• A.计算
• • 一.引例
  • • 绳索计算机
    • 尺规计算机
  • 二.算法
  • • 算法的要素
    • 程序 ≠ 算法
    • • 有穷性 引例：Hailstone
    • 什么是好算法
• B.计算模型
• • 如何进行算法分析
  • • 两个主要方面
    • 特定算法+不同实例（最坏情况）
    • 特定问题+不同算法
  • 图灵机
  • • 图灵机模型
    • 图灵机实例
    • 图灵机演示
  • RAM
  • • RAM模型
    • RAM实例
• C.渐进复杂度
• D.复杂度分析
• E.迭代与递归
• F.动态规划
• XA.局限

A.计算

一.引例

呜呜呜邓老师的字好好看！ 课件动画做的好🐮

绳索计算机

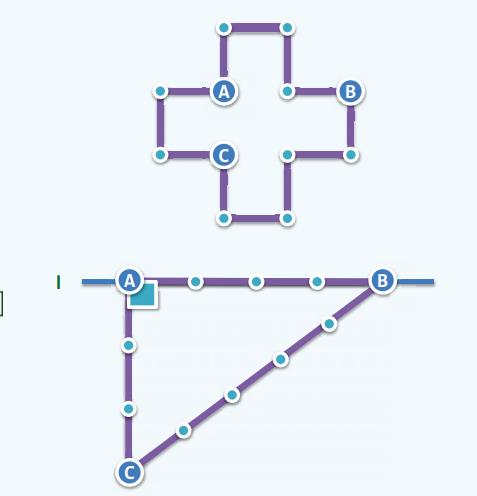
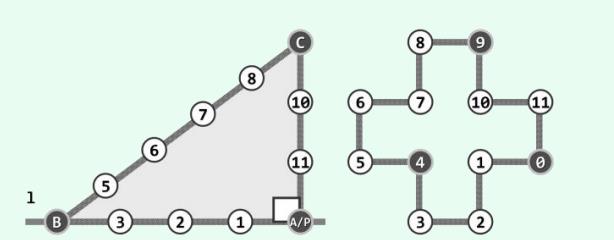
算法：过直线上给定点作直角

perpendicular(l, P)
输入：直线l及其上一点P
输出：经过P且垂直于l的直线
1. 取12段等长绳索，依次首尾联结成环 //联结处称作“结”，按顺时针方向编号为0..11
2. 奴隶A看管0号结，将其固定于点P处
3. 奴隶B看管4号结，将绳索沿直线l方向尽可能地拉直
4. 奴隶C看管9号结，将绳索尽可能地拉直
5. 经过0号和9号结，绘制一条直线

以上由古埃及人发明、由奴隶与绳索组成的这套计算工具，乍看起来与现代的电子计算机相去甚远。

但就本质而言，二者之间的相似之处远多于差异，它们同样都是用于支持和实现计算过程的物理机制，亦即广义的计算机。因此就这一意义而言，将其称作“绳索计算机”毫不过分

尺规计算机

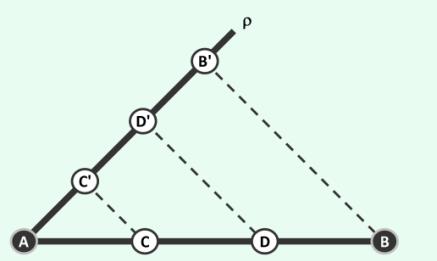
算法：三等分给定线段

tripartition(AB)
输入：线段AB
输出：将AB三等分为两个点C和D
1. 从A发出一条与AB不重合的射线p
2. 任取p上三点C'、D'和B'，使|AC'| = |C'D'| = |D'B'|
3. 联接B'B
4. 过D'做B'B的平行线，交AB于D
5. 过C'做B'B的平行线，交AB于C

这里面其实还有个子程序：过直线外一点，作平行线

二.算法

• 计算 = 信息处理 = 借助某种工具，遵照一定规则，以明确而机械的形式进行

  工具如尺规、绳索 ； 规则如尺规的使用方法

• 计算模型 = 计算机 = 信息处理工具

• 所谓算法，即特定计算模型下，旨在解决特定问题的指令序列

算法的要素

• 输入 待处理的信息（问题）

• 输出 经处理的信息（答案）

  • 正确性 的确可以解决指定的问题

  • 确定性 可描述为一个由基本操作组成的序列 //加盐少许，加糖适量，煮至半熟…

    除了上面的尺规例子，欧氏几何给出了大量过程与功能更为复杂的几何作图算法，为将这些算法变成可行的实际操作序列， 欧氏几何使用了两种相互配合的基本工具：不带刻度的直尺，以及半径跨度不受限制的圆规。同样地，从计算的角度来看，由直尺和圆规构成的这一物理机制也不妨可以称作“尺规计算机”。 在尺规计算机中，可行的基本操作不外乎以下五类：

    1过两个点作一直线
    2确定两条直线的交点
    3以任一点为圆心，以任意半径作一个圆
    4确定任一直线和任一圆的交点（若二者的确相交)
    5确定两个圆的交点（若二者的确相交)
    

    每一欧氏作图算法均可分解为一系列上述操作的组合，故称之为基本操作恰如其分

  • 可行性 每一基本操作都可实现，且在常数时间内完成 //把大象放进冰箱，不过三步… (hhh大象放入冰箱一般情况下并不可行，所以这是个不可行的算法）

  • 有穷性 对于任何输入，经有穷次基本操作，都可以得到输出

  • and …

程序 ≠ 算法

有穷性 引例：Hailstone

$$Hailstone(n)=\{\begin{array}{ll}1& (n\le 1)\\ n\cup \text{ Hailstone }(n/2)& (n\text{ is even })\\ n\cup \text{ Hailstone }(3n+1)& (n\text{ is odd })\end{array}$$

Hailstone(42)= 42，21，64，32,…， 1

int hailstone(int n) //计算序列Hailstone(n)的长度
	int length = 1;//从1开始，以下按定义逐步递推，并累计步数，直至n = 1
	while (1 <n)  (n % 2 ? n = 3 * n + 1 :n /= 2; length++; 
	return length;//返回 | Hailstone(n)|

上面这个程序看似很对，但是能称之为算法吗？

我们可以发现一些问题，比如n 与 length并不成正比

还有，它满足有穷性吗？ 这个取决于hailstone序列本身

对于任意的 n ，总有$\mid Hailstone(n)\mid <\infty 吗?$ 目前还木有结论，所以上面那个程序未必是一个算法

💭程序未必是算法

• 配套的excel演示资源太帅啦！

  

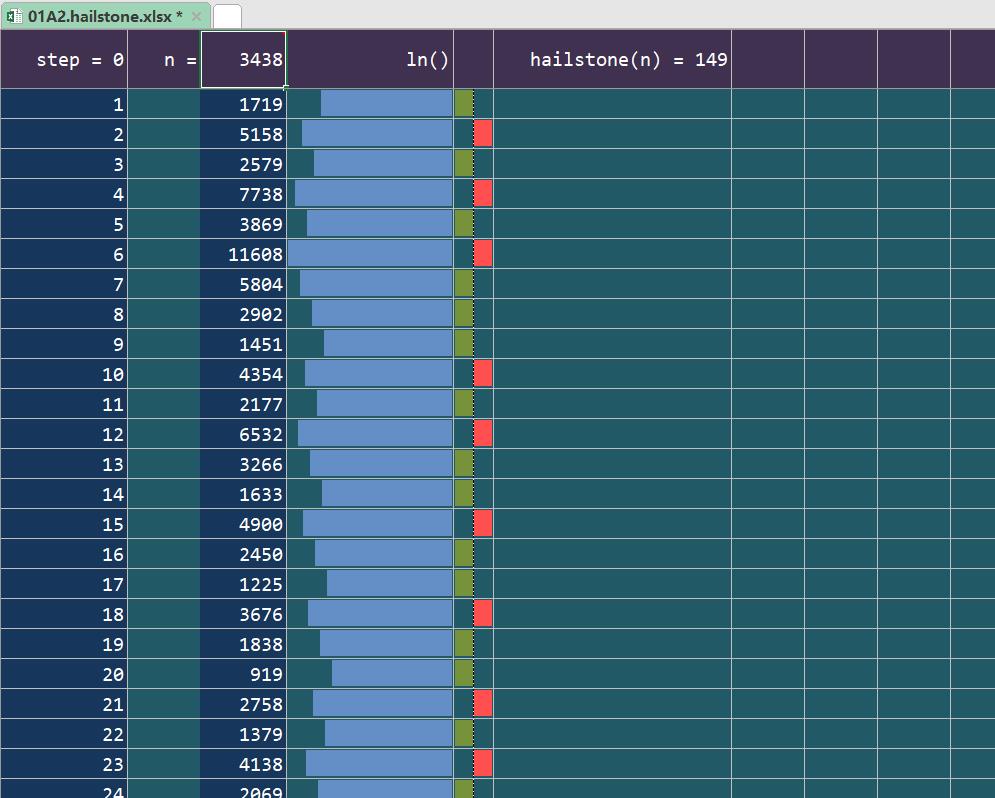
什么是好算法

这一部分主要是树立观念

• 符合语法，能够编译、链接

  • 能够正确处理简单的输入
  • 能够正确处理大规模的输入
  • 能够正确处理一般性的输入
  • 能够正确处理退化的输入
  • 能够正确处理任意合法的输入

• 健壮： 能辨别不合法的输入并做适当处理 而不致非正常退出

• 可读： 结构化 + 准确命名 + 注释 + …

• 效率： 速度尽可能快 存储空间尽可能少 （most important！）

  hhh 既要马儿快快跑，又要马儿吃得少（

  • Algorithms + Data Structures = Programs
  • (Algorithms + Data Structures) x Efficiency = Computation

B.计算模型

如何进行算法分析

• 有效性和高效性的前提是数据结构和算法两方面的有机结合，DSA(data structure and algorithm)

  • 定性：DSA的好坏取决于它的效率

  • 但实际应用中还需要度量，需要定量

    hhh 邓老师引用了好多名言

    To measure is to know.

    If you cannot measure it, you can not improve it. -Lord Kelvin

• so，we need to 找到一个 统一尺度

两个主要方面

• 正确：算法功能与问题要求一致？ 需要数学证明

• 成本：运行时间 + 所需存储空间 如何度量？如何比较？

  • 这里主要讨论成本 ，并主要先讨论时间成本

• 若将计算成本描述为函数，如

  $T_A(P)$=算法A求解问题实例P的计算成本，但这样意义不大

  因为一个问题可能有很多实例，某个实例容易以偏概全

  所以要对实例粗略分类，划分等价类

• 一般情况下（不绝对），问题实例的规模，往往是决定计算成本的主要因素

• 通常：

  • 规模接近，计算成本也接近
  • 规模扩大，计算成本亦上升

特定算法+不同实例（最坏情况）

• 在经过上面所说的等价类划分后，我们就可以重新将刚才那样一个数学的度量形式进行改写

  令： $T_A(n)$ = 用算法A求解某一问题规模为n的实例，所需的计算成本

  • 和前面$T_A(P)$最大的不同就在于把原来每一个具体的问题实例P，变成了笼统而言的一个规模的度量值，也就是n。也就是我们可以把某一个算法在求解规模为 n 的一大类实例的过程中，他们各自所需要的时间成本笼统计作$T_A(n)$。我们如果暂时把算法固定，讨论特定算法A（及其对应的问题）时，也可以把 A 忽略掉，可简记作$T(n)$

• However，这样的定义依然不能满足我们实际的需求，不足以支撑我们分析的需要

  • Why？👇

  • 对于同一问题，即便是规模接近甚至相等的输入实力，计算成本虽然大体是差不多的，但是毕竟还是有差异，甚至会有实质性的差异。

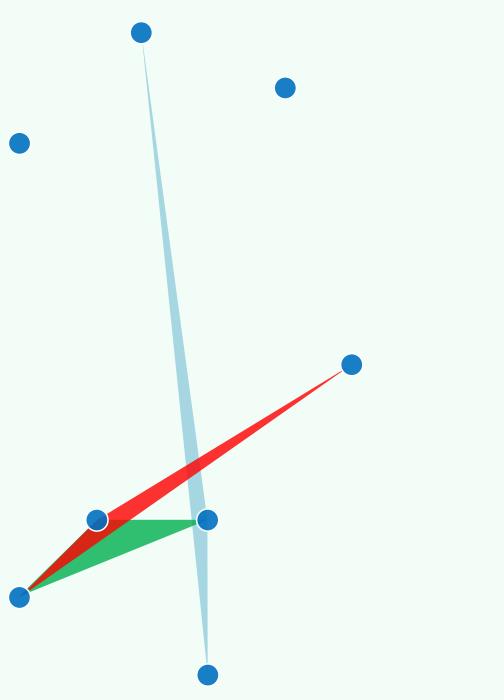
  • 任给平面上n个点，在它们定义的 $\left(\begin{array}{l}n\\ 3\end{array}\right)$ 个三角形中， 找出其中面积最小的三角形

    • 假设在平面中随便给定 n 个点（这里的 n 就是输入规模），我们知道其中的任何三个点都会定义一个三角形
    • 如果不知道技巧的话，不妨采用所谓的蛮力算法，也就是逐一的去枚举所有 n 中取 3 的组合，分别的算出它们各自对应的面积，并保留和记录下最后整体的最小值
    

  • 这个算法是正确的，但是我们这样固定的一个算法，对于不同的 n 个点的组合，有可能尝试的运气是不一样的，所需要的成本有很大的区别。

    • 比如在最坏的情况下，可能会直到把所有的组合都尝试变后，在最后才会找到最小的三角形
    • 但是反过来是欧皇的时候，可能第一次枚举的 3 个点就是共线的，面积为0，面积不可能是负值。这时已经找到了问题的解。
    • 所以我们可以看到同样规模为 n 的那些实例所需要的计算成本是有天壤之别。
      • Hailstone的例子，也是这样的一个情况。

• 既然这样，那么我们又该如何去定义我们刚才所给出来的$T(n)$ ？

  • 显然，我们不能把命运寄托在最好的情况下，稳妥起见，应更关注一个算法的最坏情况。

  • 稳妥起见，取 $T(n)=\\max T§\\big|\\small| P \\small|=n\\$

    • 亦即，在规模同为 n 的所有实例中，首先关注最坏（成本最高）者

特定问题+不同算法

在解决了特定算法的评价问题之后，我们就需要进一步的来回答另一个问题，也就是当同一个问题拥有多个算法的时候，这是经常出现的情况。我们如何来评价它们之间的相对好坏或者优劣？

• 同一问题通常有多种算法，如何评判其优劣？

• 实验统计是最直接的方法，但足以准确反映算法的真正效率？不足够！

  不同的算法各有所长，也各有所短。如果我们的测试在问题实例的规模以及类型等等方面覆盖的不够全面，不具有充分的代表性。这种测试本身就是带有偏见的，它的结论也难以让人信服

  • 不同的算法，可能更适应于不同规模的输入
  • 不同的算法，可能更适应于不同类型的输入

  即使是同一算法

  • 同一算法，可能由不同程序员、用不同程序语言、经不同编译器生成

    即便是由同一个程序员用同一种语言，并且用同一种编译器和设置编译出来的执行代码。在不同的硬件体系结构上，在不同操作系统上体现出来的性能，在此时和彼时也可能有很大的区别。比如硬件的 CPU 速度，内存的和磁盘的速度和容量，以及它们之间的带宽等等。包括操作系统在不同的时刻对不同计算资源分配的当时的状况不同等等。

  • 同一算法，可能实现并运行于不同的体系结构、操作系统…

  这些因素都不可能有限次实验统计就足以覆盖

• 为给出客观的评判，需要抽象出一个理想的平台或模型

  我们需要抽象出一种理想的计算平台或者模型，为此才能抛开上述种种，具体的其实是次要的因素，更加直接和准确的来评价和测量算法。最后得出一个客观的结论

  • 不再依赖于上述种种具体的因素
  • 从而直接而准确地描述、测量并评价算法

  人们已经构造出了多种这样的理想的平台和模型。比如我们接下来要讨论的图灵机模型

图灵机

图灵机模型

图灵机实例

图灵机演示

RAM

RAM模型

RAM实例

C.渐进复杂度

D.复杂度分析

E.迭代与递归

F.动态规划

XA.局限