分别使用specgram函数和tftb工具箱对信号进行STFT短时傅里叶时频分析matlab仿真

Posted 2022-12-15 fpga和matlab

up目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       傅里叶变换只反映出信号在频域的特性，无法在时域内对信号进行分析。为了将时域和频域相联系，Gabor于1946年提出了短时傅里叶变换(short-time Fourier transform，STFT)，其实质是加窗的傅里叶变换。STFT的过程是：在信号做傅里叶变换之前乘一个时间有限的窗函数 h(t)，并假定非平稳信号在分析窗的短时间隔内是平稳的，通过窗函数 h(t)在时间轴上的移动，对信号进行逐段分析得到信号的一组局部“频谱”。信号的短时傅里叶变换定义为：

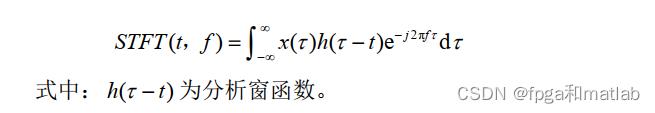
        然而，傅里叶变换是一种全局的变换，时域信号经过傅里叶变换后，就变成了频域信号，从频域是无法看到时域信息的，我们可以从上节中的傅里叶变换和反变换公式进行解释，进行正变换时，积分区间为整个时域，所以变换结果将不包含时域信息，反变换同理。

       如果信号的频率特性在任何时间都不发生改变(即该信号是平稳信号)的话，使用傅里叶变换是没有问题的，然而如果该信号是非平稳信号，这时候时域信息就相当重要了。举个栗子，以下分别是0~100Hz线性递增扫频信号和100~0Hz线性递减扫频信号的幅度谱，这两个信号都是非平稳信号，可以看到它们的幅度谱是相同的，很显然我们无法知道每一个频率分量出现的时间，即无法知道扫频信号的模式。

       分析时域可以得到信号随时间变化的信息，分析频域可以得到信号随频率变化的信息，这两者都只能分析时域或频域，而不能同时观察时域和频域。

        时频分析是时频联合域分析的简称，是分析时变非平稳信号的有力工具，是一个同时观察时域、频域信息的工具。时频分析法提供了时间域和频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系。

        时频分析的基本思想是：设计时间和频率的联合函数，用它同时描述信号在不同时间和频率的能量密度或强度。

        时间和频率的这种联合函数简称为时频分布。利用时频分布来分析信号，能给出各个时刻的瞬时频率和幅值。

        常见的时频分布有：短时傅里叶变换、小波变换、希尔伯特黄变换等。

其中，STFT理论如下所示：

二、核心程序

%这是一个利用tfrstft函数进行STFT分析的程序
%生成两个chirp信号，一个频率由小变大，另一个由大变小，将两者相加，求其STFT时频谱
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
t=0:0.001:1.024-.001;
N=1024;
%两个chirp信号，并相加：
y1=chirp(t,0,1,350);
y2=chirp(t,350,1,0);
y=y1+y2;
%求两个chirp信号的短时傅里叶变换；
ym=y';
tfrstft(ym);

function [tfr,t,f] = tfrstft(x,t,N,h,trace);
 
[xrow,xcol] = size(x);
if (nargin < 1),
 error('At least 1 parameter is required');
elseif (nargin <= 2),
 N=xrow;
end;

hlength=floor(N/4);
hlength=hlength+1-rem(hlength,2);

if (nargin == 1),
 t=1:xrow; h = tftb_window(hlength); trace=0;
elseif (nargin == 2) | (nargin == 3),
 h = tftb_window(hlength); trace = 0;
elseif (nargin == 4),
 trace = 0;
end;

if (N<0),
 error('N must be greater than zero');
end;
[trow,tcol] = size(t);
if (xcol~=1),
 error('X must have one column');
elseif (trow~=1),
 error('T must only have one row'); 
elseif (2^nextpow2(N)~=N),
 fprintf('For a faster computation, N should be a power of two\\n');
end; 

[hrow,hcol]=size(h); Lh=(hrow-1)/2; 
if (hcol~=1)|(rem(hrow,2)==0),
 error('H must be a smoothing window with odd length');
end;

h=h/norm(h);

tfr= zeros (N,tcol) ;  
if trace, disp('Short-time Fourier transform'); end;
for icol=1:tcol,
 ti= t(icol); tau=-min([round(N/2)-1,Lh,ti-1]):min([round(N/2)-1,Lh,xrow-ti]);
 indices= rem(N+tau,N)+1; 
 if trace, disprog(icol,tcol,10); end;
 tfr(indices,icol)=x(ti+tau,1).*conj(h(Lh+1+tau));
end;
tfr=fft(tfr); 
if trace, fprintf('\\n'); end;

if (nargout==0),
 tfrqview(abs(tfr).^2,x,t,'tfrstft',h);
elseif (nargout==3),
 if rem(N,2)==0, 
  f=[0:N/2-1 -N/2:-1]'/N;
 else
  f=[0:(N-1)/2 -(N-1)/2:-1]'/N;  
 end;
end;

三、测试结果

使用matlab2021a仿真测试结果如下所示：

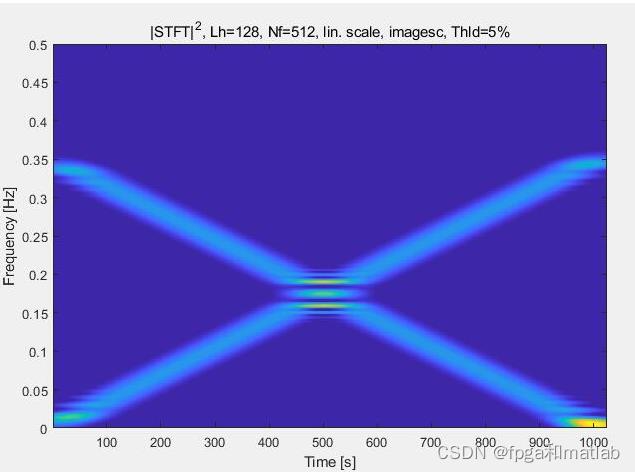
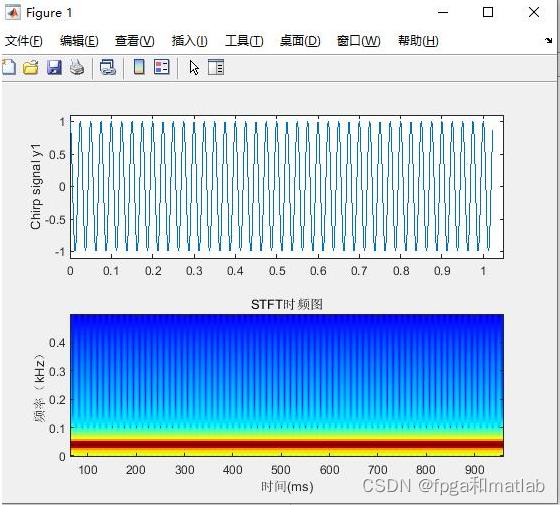
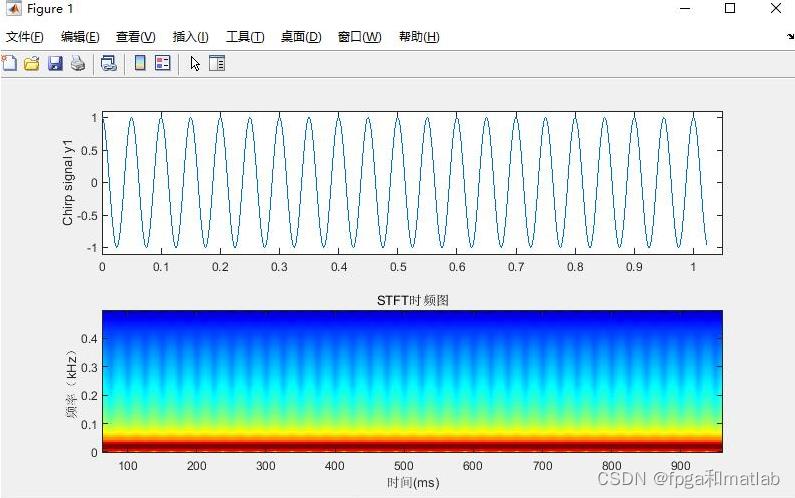
up0007