递归：递归的理解与应用

Posted 2022-12-14 我家大宝最可爱

什么是递归算法

递归算法就是将原问题不断分解为规模缩小的子问题，然后递归调用方法来表示问题的解。（用同一个方法去解决规模不同的问题）

• 递去：将递归问题分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决
• 归来：当你将问题不断缩小规模递去的时候，必须有一个明确的结束递去的临界点（递归出口），一旦达到这个临界点即就从该点原路返回到原点，最终问题得到解决。
  四、递归算法的设计要素

递归算法的难点就在于它的逻辑性，一般设计递归算法需要考虑以下几点:

1. 明确递归的终止条件
2. 提取重复的逻辑，缩小问题的规模不断递去
3. 给出递归终止时的处理办法

下面给出我自己对递归的理解

递去有两层含义

1. 假设子问题已经完成了求解，我们可以直接使用子问题的解
2. 子问题已经缩到了最小规模，也就是常说的终止条件

归来有两层含义

1. 子问题已经缩小为最小规模，即到达了停止条件
2. 根据子问题的解和入参来求解原问题，也就是递归的逻辑代码

1. 子问题与原问题是否是一致的，子问题是否只是缩小了问题的规模
2. 如果原问题的解不依赖于子问题的解，这个问题肯定不用递归，否则可以考虑递归
3. 假设子问题已经解决了，这个时候如何将入参与子问题的解进行逻辑处理，从而得到原问题的解

递归的理解

1. 递归的执行顺序

举个具体的例子来看看什么是递归，假如有一个排学员，教官让每个人抱自己的名字，

规则非常的简单，先报自己的名字，然后问下一个人叫什么，下一个继续报自己的名字，然后不断往后

# 先报自己名字，再问后面叫啥
def whatsName(head):
	if nobody: stop # 后面没人就停下了
	print(head.name) # 先报自己名字
	signal = whatsName(head.next) # 再问后面叫啥
	# 不管收到啥信号，反正收到我就回复over
	return 'over'

收集到的名字就是：小中，小华，小五，小千，小年，这个时候教官说我们改一下规则，先问后面叫什么，等后面的人回答了再报自己的名字

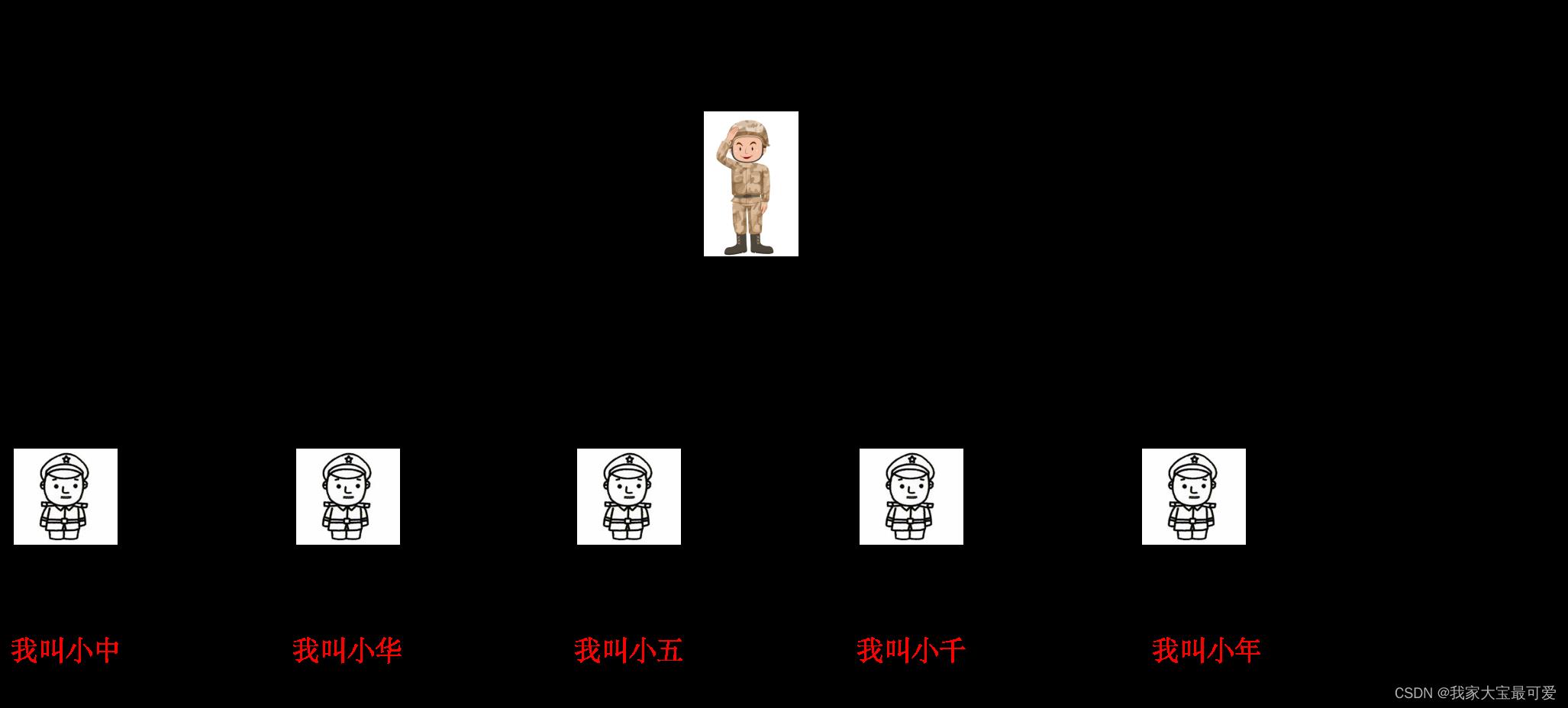
这个时候就很有意思了，是最后一个人先回答的，然后层层传回去，所以搜集到名字就是：小年，小千，小五，小华，小中。我们发现与之前的顺序正好相反。

# 先问后面叫啥，回应后再报自己名字
def whatsName(head):
	if nobody: stop # 后面没人就停下了
	signal = whatsName(head.next) # 先问后面叫啥
	if signal == 'over': # 后面的人说完再报自己的名字
		print(head.name)
	return 'over' # 报完自己名字之后也要返回over给前面的人

从上面这个例子我们可以发现，递归就是不断深入下去，当遇到终止条件之后再开始层层返回，

• 如果先处理再递归，此时就是顺序往下执行
• 如果是先递归再处理，那么此时就是逆序执行

2. 递归的子问题

每个士兵都有自己的战力值，所有士兵的战力值之和就是团队战力值，现在教官想要知道团队战力值，就让第一个士兵统计整个团队的战力。
第一个士兵很懒，所以想了一个办法，他让第二个士兵去统计后面所有人的战力值，等到汇总给自己之后再加上自己的战力就可以了，第二个士兵也是这么想的。。。

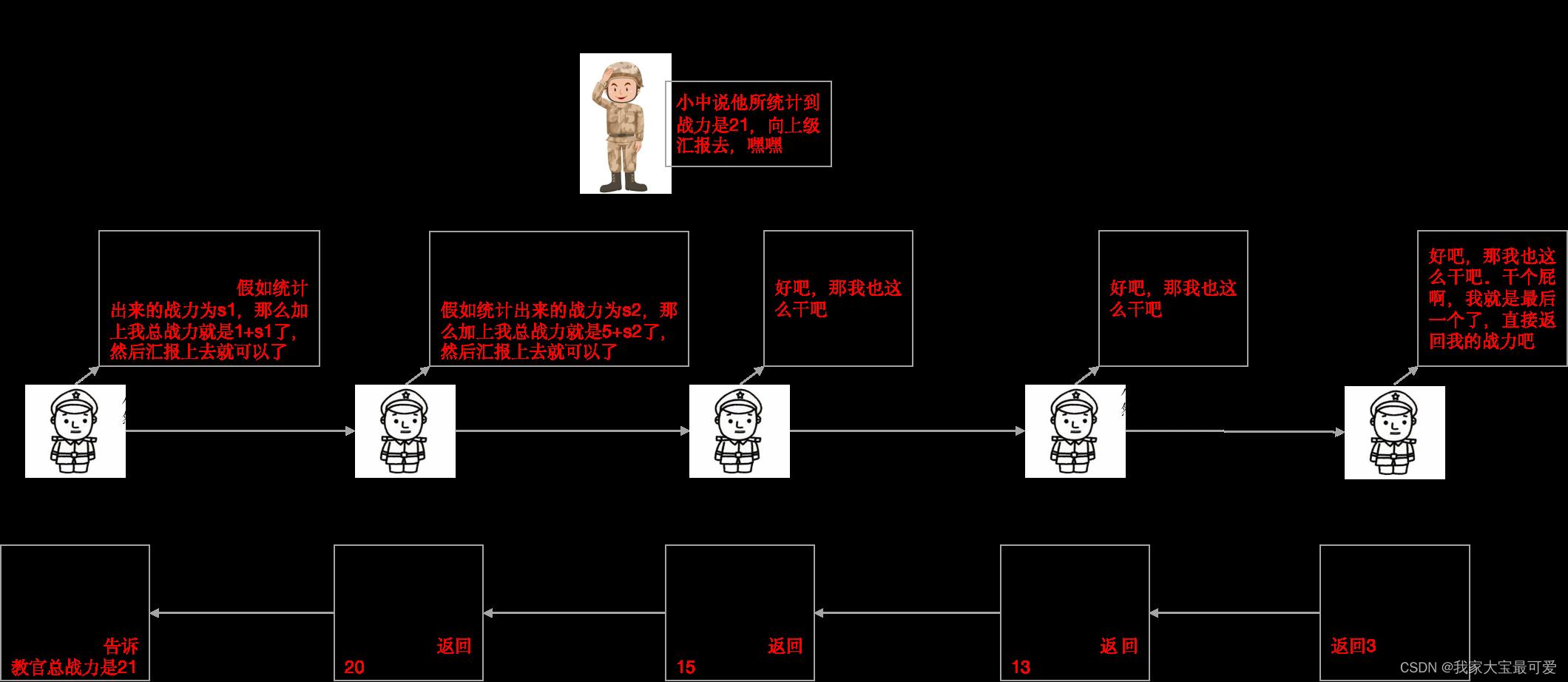
递归有一个非常有意思的地方，就是假设子问题已经解决了，然后根据子问题和其余参数去解决原问题。而且由于是递归，每个人都认为是自己那个head，以为自己是原问题的解，其实也只是套娃中的一层而已，不断的返回去，直至结束。

def get_score(head):
	if head is None: return 0
	s = get_score(head.next) # 先让后面人统计
	return head.val + s # 再加上自己去返回

这里其实就很奇怪，递归怎么知道问题已经求解完成了呢？这就不得不说递归的本质栈，每进入一层递归函数，操作系统就会把当前的参数保存下来，然后等到遇到递归的终止条件之后再出栈

3. 递归的逻辑结构

这一天教官要检查团队每个人成员的成绩是否达标，一旦有一个人不达标，那么整个团队就不达标，同样的，教官把这个艰巨的任务交给了小中，小中心想这还不简单吗，

1. 先让小华去统计后面的人是否都合格了
2. 检查自己是不是都合格，然后返回总结果
   

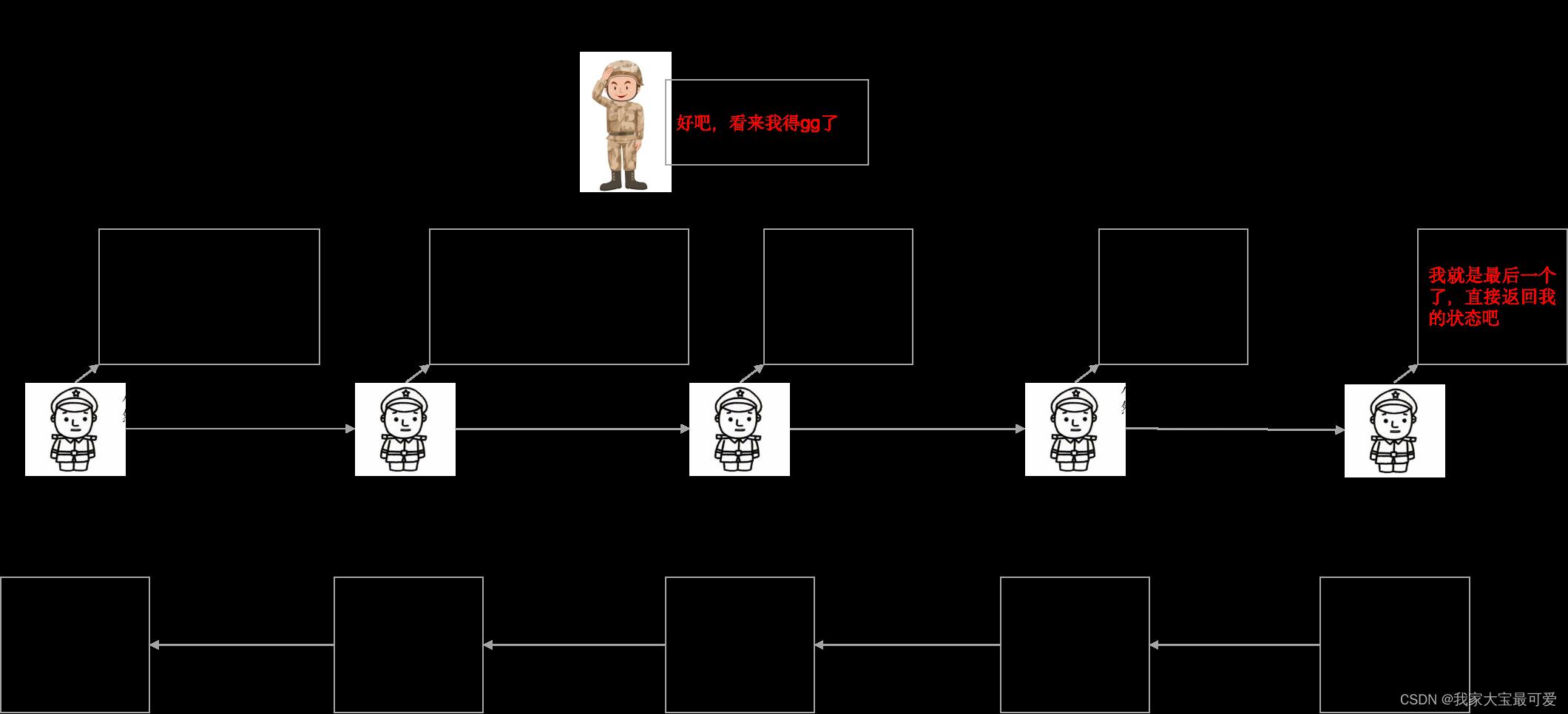
def isAllOk(head):
	if head is None: return True
	sr = isAllOk(head.next) # 等下一个人告诉我是否都合格
	return head.val and sr # 结合自身情况返回

可以发现这个问题与求战力和的过程是一模一样的，但是在处理过程中我发现了更简单的一个办法。

1. .先检查自身是否合格了，如果不合格就直接返回gg
2. 如果自身合格了，再要求小华去检查其他人，否则根本不需要去求子问题
   

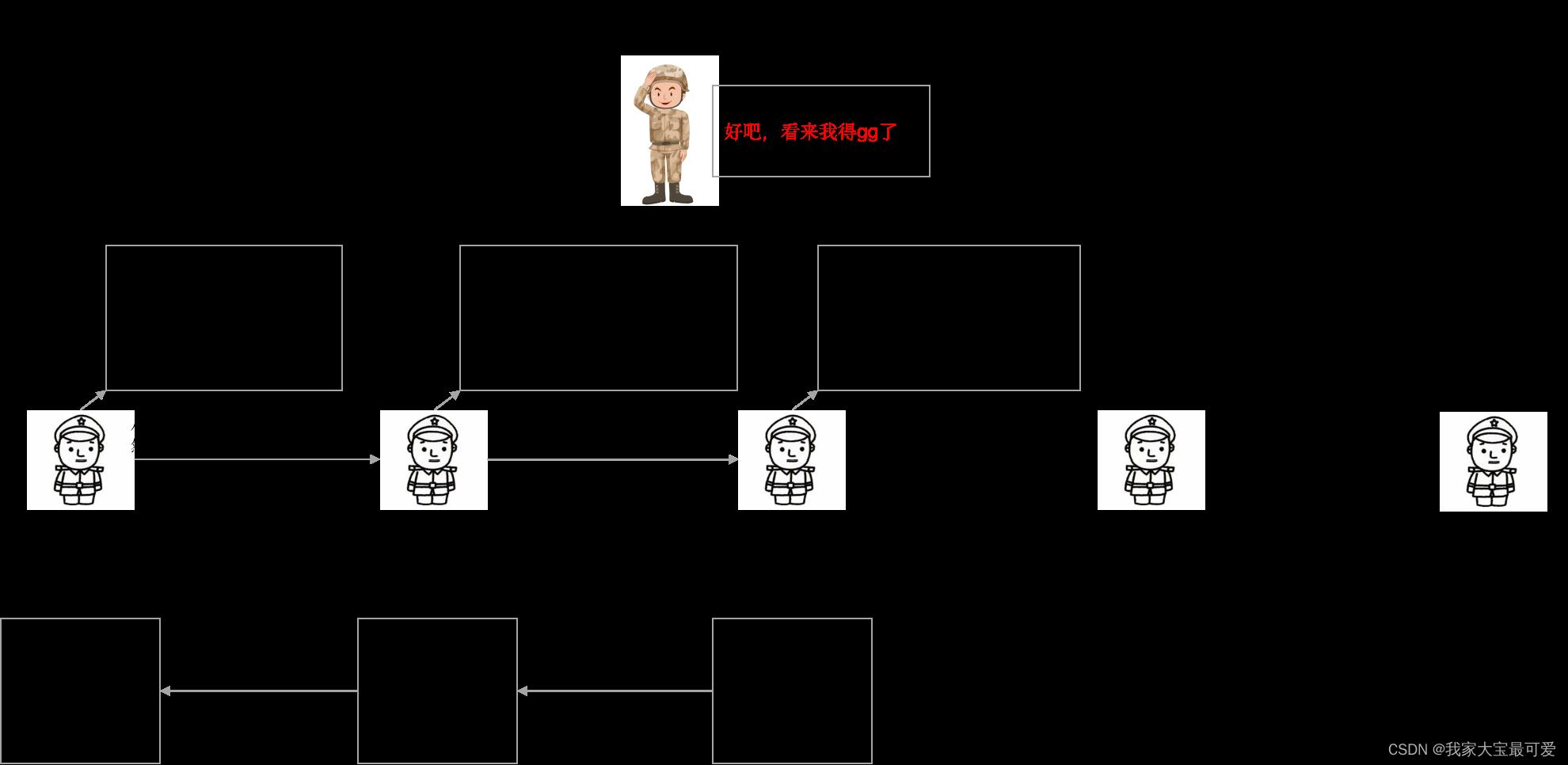
def isAllOk(head):
	if head is None: return True
	if head.val:
		sr = isAllOk(head.next) # 等下一个人告诉我是否都合格
		return sr
	return False

很有意思，我们发现通过条件语句可以控制子问题的深度

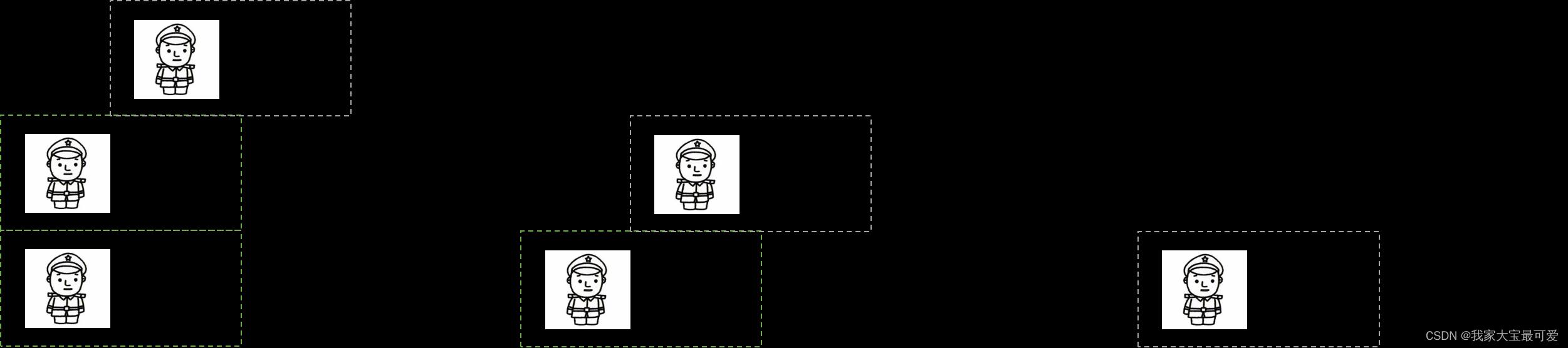
我把上面的代码再换一下顺序，更好理解了。当前是False，那么直接就返回False，否则就返回子问题的解

def isAllOk(head):
	if head is None: return True
	if not head.val: return False
	return isAllOk(head.next) # 等下一个人告诉我是否都合格

4. 子问题的定义

前面可以看到数据结构基本都是链表，原问题是整个链表的解，子问题是子链表的解。

5. 递归的返回

如果原问题要求返回的结果是一个数组，那么子问题返回的结果是什么？肯定是一个数组，因为子问题与原问题又相同的结果，所以返回的肯定也是相同，终止条件返回什么？肯定也是一个数组，因为终止条件就是最小的子问题。

def func(exp):
	if conditon: return init_res
	do_something(exp)
	sub_res = func(?exp)
	do_something(exp, sub_res)
	return res

其中init_res, sub_res, res终止条件的返回，子问题的返回，原问题的返回，他们的数据结构肯定是一样的。放在这里讨论递归的返回其实已经有点晚了，只能说慢慢思考吧