机器学习-决策树(decision tree)算法

Posted 2022-12-14 YEN_csdn

学习彭亮《深度学习基础介绍：机器学习》课程
[toc]

决策树概念

决策树是一种用于监督学习的层次模型，由此，局部区域通过少数几步递归分裂决定。
决策树是一个类似流程图的树结构：其中每个结点表示在一个属性上测试，每个分支代表一个属性输出，每个树叶结点代表类或类分布。树的最顶层是根节点。

信息熵entropy概念

一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息 => 信息量的度量就等于不确定性的多少

比特(bit)来衡量信息的多少
-[P1*log2(P1)+P2*log2(P2)+…+Pn*log2(Pn)] (其中Pi：i发生的概率)
变量的不确定性越大，熵也就越大

决策树算法

• 分类与回归树（classification and regression,CART）算法
• ID3算法
• C4.5算法（ID3算法的扩展）

相同点：都是贪心算法，自上而下
区别：信息度量方法不一样： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

决策树归纳算法实例 （ID3）

选择属性判断结点：信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D)，通过A来作为节点分类获取了多少信息

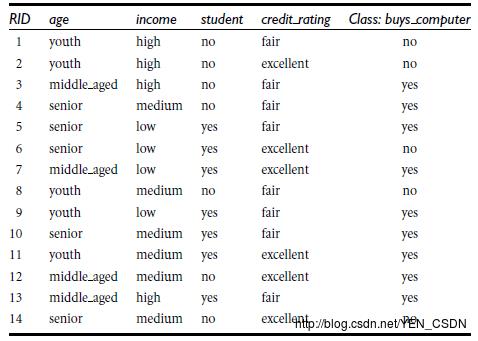
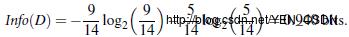
假设以年龄（youth）来分

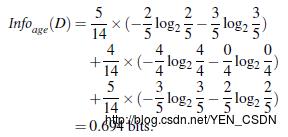
14个人中年轻人（youth）有5个： P1=5/14 ,在5个人中yes有两个，no有三个

在没有用年龄区分是信息熵为0.940bit，用年龄区分信息熵为0.694bit，所以以年轻人来分信息获取量为：

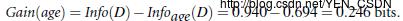
同理：
根据收入信息获取量：Gain(income)=0.029
根据学生信息获取量：Gain(student)=0.151
根据信用信息获取量：Gain(Credit_rating)=0.048

所以以age信息获取量最大，取它做为第一个节点，

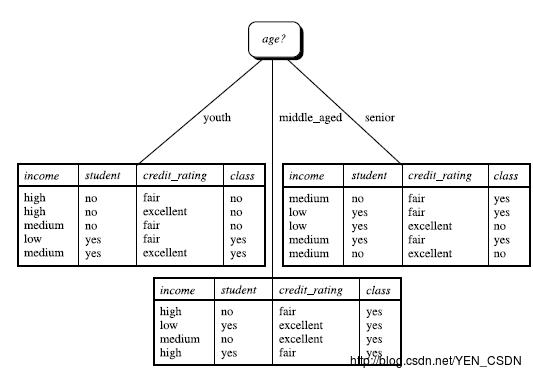
下一步在选取新的属性来做为新结点，同样计算谁能带来最大的信息获取量。重复进行。

注：连续型要离散化处理。

剪枝

• 先剪枝
• 后剪枝，实践中比先剪枝效果好。
  在后剪枝中，我们让树完全增长至所有树叶都是纯的并具有零训练误差。然后，我们找出导致过分拟合的子树并剪掉它。

决策树优缺点

• 优点：直观；便于理解；小规模数据集有效
• 缺点：处理连续变量不好；类别较多时，增加的比较快；可规模性一般

决策树归纳算法实例代码 （Python）

Python机器学习的库：scikit-learn
覆盖问题领域：分类（classification), 回归（regression), 聚类（clustering), 降维(dimensionality reduction)，模型选择(model selection), 预处理(preprocessing)

代码

#coding=utf-8
# @Author: yangenneng
# @Time: 2018-01-09 16:17
# @Abstract：Decision_Tree.py   决策树应用

# DictVectorizer： 读取原始数据
import csv
# 导入机器学习包

# DictVectorizer： 将dict类型的list数据，转换成numpy array
from sklearn.feature_extraction import DictVectorizer
from sklearn import tree
from sklearn import preprocessing
from sklearn.externals.six import StringIO

# 主程序

#读取使用的数据文件
allElectroncsData=open(r'D:\\Python\\PyCharm-WorkSpace\\MachineLearningDemo\\Decision_Tree\\data\\buyComputer.csv','rb')
#csv中按行读取函数reader()
reader=csv.reader(allElectroncsData)
headers=reader.next() #读取第一行标题

# print (headers)

featureList=[]  # 装取特征值
lableList=[]    # 装取类别 buy:yes|no

#逐行读取
for row in reader:
    lableList.append(row[len(row)-1]) #每行最后一列的值加入lableList
    rowDict= #字典 key为对并的属性名:eg：age  value为属性值：eg：youth
    for i in range(1,len(row)-1):
        rowDict[headers[i]]=row[i]

    featureList.append(rowDict)

# print featureList

#使用python提供的DictVectorizer()进行转化我们需要的特征值dummyx格式
vec=DictVectorizer()
dummyx=vec.fit_transform(featureList).toarray()

# print ("dummyx:"+str(dummyx))
# print (vec.get_feature_names())

# print ("lableList:",str(lableList))

#使用python提供的DictVectorizer()进行转化我们需要的分类dummyy格式
lb=preprocessing.LabelBinarizer()
dummyy=lb.fit_transform(lableList)

# print ("dummyy:"+str(dummyy))

# using decision tree for classfication

# 使用ID3算法，即用Information Gain来分类
clf=tree.DecisionTreeClassifier(criterion='entropy')
# 建模   参数：特征值矩阵 分类列矩阵
clf=clf.fit(dummyx,dummyy)

# print ("clf",str(clf))

# 产生dot文件
with open("allElectroncInfomationGainori.dot",'w') as f:
    # 原始的数据变为0 1了，再画决策树时要还原之前定义的feature，即feature_names=vec.get_feature_names()
    f=tree.export_graphviz(clf,feature_names=vec.get_feature_names(),out_file=f)
# 取第一行
oneRowX=dummyx[0,:]
print ("oneRowX:"+str(oneRowX))

#预测新数据
newRowx=oneRowX
newRowx[0]=1
newRowx[2]=0

print ("newRowx:"+str(newRowx))

predictedY=clf.predict(newRowx)
print  ("predictedY:"+str(predictedY))

数据

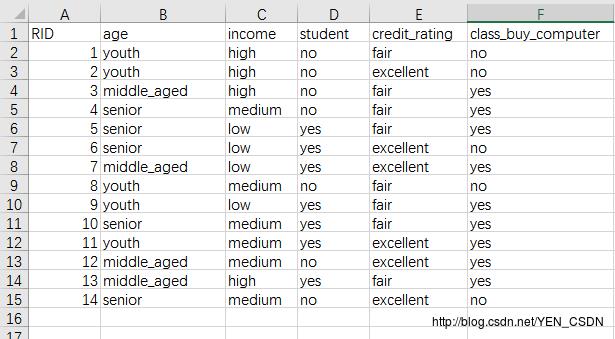
需把每一行进行转化为以下格式：

print featureList

print ("dummyx:"+str(dummyx))
print (vec.get_feature_names())
print ("lableList:",str(lableList))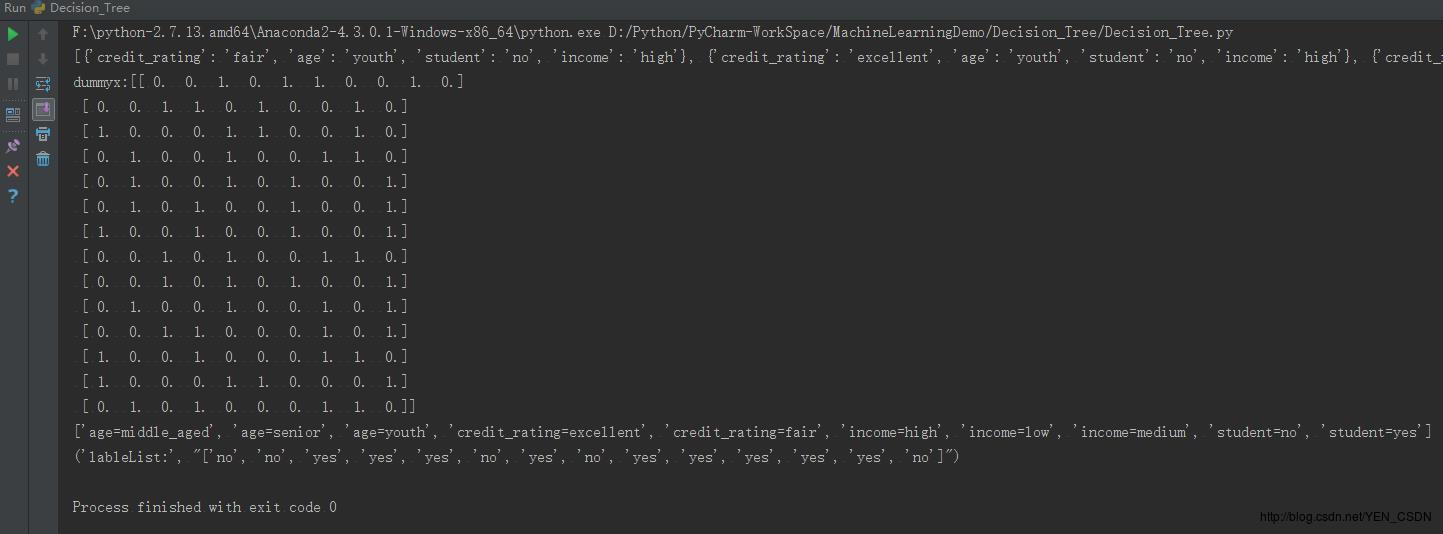

print ("dummyy:"+str(dummyy))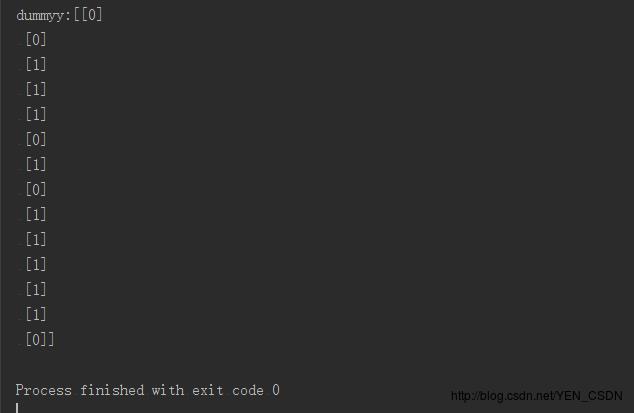

print ("clf",str(clf))

print ("oneRowX:"+str(oneRowX))

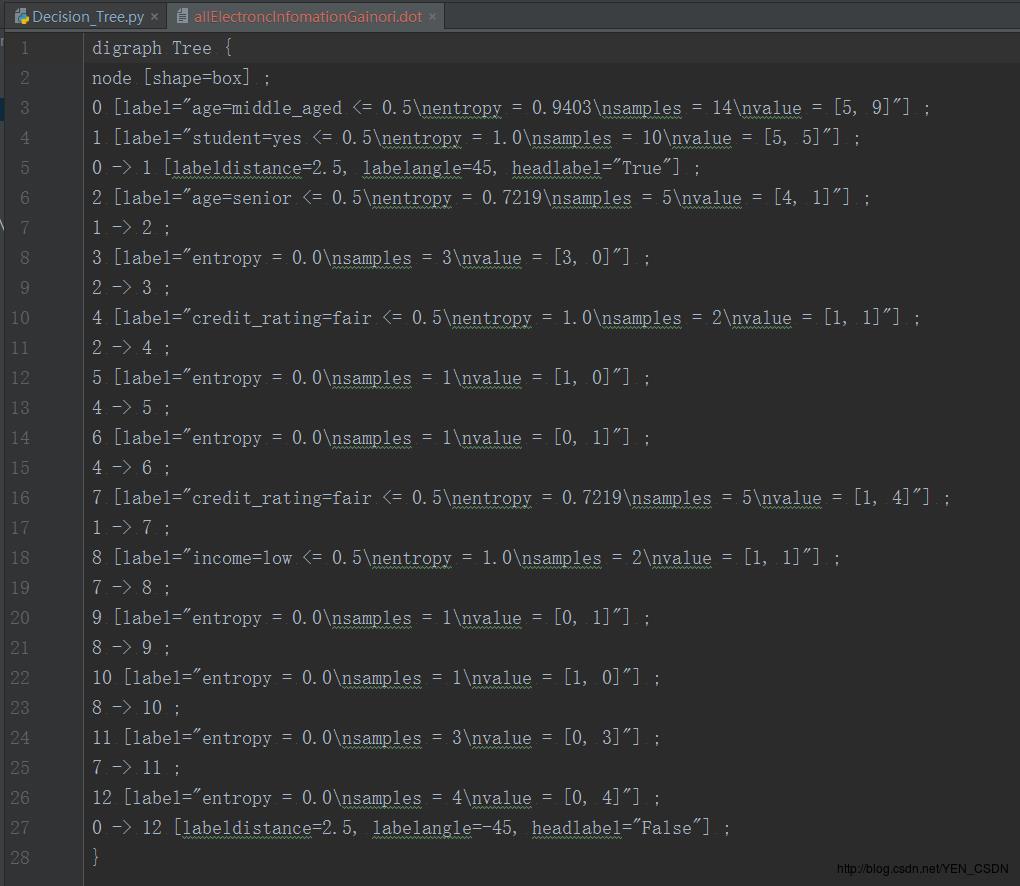
得到的allElectroncInfomationGainori.dot

#预测新数据
newRowx=oneRowX
newRowx[0]=1
newRowx[2]=0

print ("newRowx:"+str(newRowx))

predictedY=clf.predict(newRowx)
print  ("predictedY:"+str(predictedY))

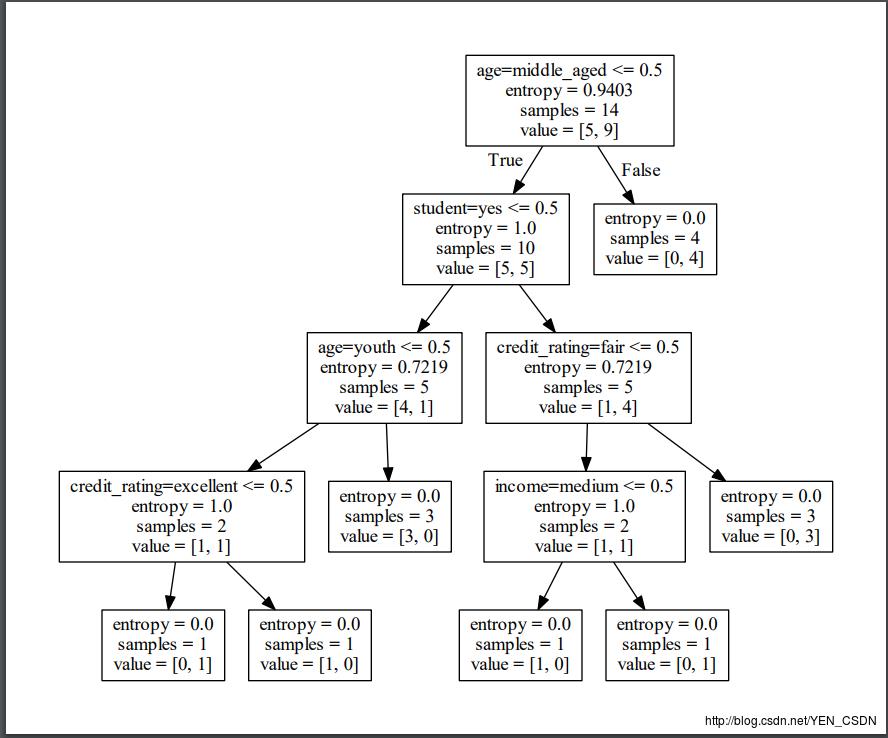
使用graphviz转为PDF决策树

安装graphviz：https://graphviz.gitlab.io
配置环境变量，转化dot文件至pdf可视化决策树：dot -Tpdf 文件名.dot -o 文件名.pdf