机器学习：AnomalyDetection异常检测_Python

Posted 2022-12-11 莫失莫忘Lawlite

七、异常检测 Anomaly Detection

• github地址：https://github.com/lawlite19/MachineLearning_Python
• 全部代码

1、高斯分布（正态分布）Gaussian distribution

• 分布函数：
  
  • 其中，u为数据的均值，σ为数据的标准差
  • σ越小，对应的图像越尖
• 参数估计（parameter estimation）
  
  • 
  • 

2、异常检测算法

• 例子
  
  • 训练集：,其中
  • 假设相互独立，建立model模型：
• 过程
  
  • 选择具有代表异常的feature:xi
  • 参数估计：
  • 计算p(x),若是P(x)<ε则认为异常，其中ε为我们要求的概率的临界值threshold
• 这里只是单元高斯分布，假设了feature之间是独立的，下面会讲到多元高斯分布，会自动捕捉到feature之间的关系
• 参数估计实现代码

# 参数估计函数（就是求均值和方差）
def estimateGaussian(X):
    m,n = X.shape
    mu = np.zeros((n,1))
    sigma2 = np.zeros((n,1))

    mu = np.mean(X, axis=0) # axis=0表示列，每列的均值
    sigma2 = np.var(X,axis=0) # 求每列的方差
    return mu,sigma2

3、评价p(x)的好坏，以及ε的选取

• 对偏斜数据的错误度量

  • 因为数据可能是非常偏斜的（就是y=1的个数非常少，(y=1表示异常)），所以可以使用Precision/Recall，计算F1Score(在CV交叉验证集上)
  • 例如：预测癌症，假设模型可以得到99%能够预测正确，1%的错误率，但是实际癌症的概率很小，只有0.5%，那么我们始终预测没有癌症y=0反而可以得到更小的错误率。使用error rate来评估就不科学了。
  • 如下图记录：
    
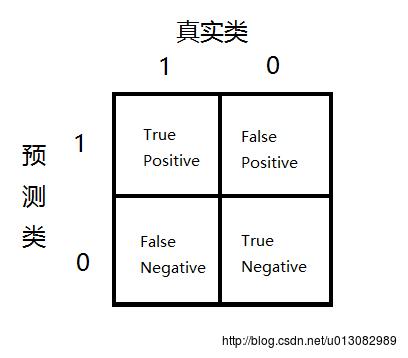
  • ，即：正确预测正样本/所有预测正样本
  • ，即：正确预测正样本/真实值为正样本
  • 总是让y=1(较少的类)，计算Precision和Recall
  • 
  • 还是以癌症预测为例，假设预测都是no-cancer，TN=199，FN=1，TP=0，FP=0，所以：Precision=0/0，Recall=0/1=0，尽管accuracy=199/200=99.5%，但是不可信。

• ε的选取

  • 尝试多个ε值，使F1Score的值高
• 实现代码

# 选择最优的epsilon，即：使F1Score最大    
def selectThreshold(yval,pval):
    '''初始化所需变量'''
    bestEpsilon = 0.
    bestF1 = 0.
    F1 = 0.
    step = (np.max(pval)-np.min(pval))/1000
    '''计算'''
    for epsilon in np.arange(np.min(pval),np.max(pval),step):
        cvPrecision = pval<epsilon
        tp = np.sum((cvPrecision == 1) & (yval == 1)).astype(float)  # sum求和是int型的，需要转为float
        fp = np.sum((cvPrecision == 1) & (yval == 0)).astype(float)
        fn = np.sum((cvPrecision == 1) & (yval == 0)).astype(float)
        precision = tp/(tp+fp)  # 精准度
        recision = tp/(tp+fn)   # 召回率
        F1 = (2*precision*recision)/(precision+recision)  # F1Score计算公式
        if F1 > bestF1:  # 修改最优的F1 Score
            bestF1 = F1
            bestEpsilon = epsilon
    return bestEpsilon,bestF1

4、选择使用什么样的feature（单元高斯分布）

• 如果一些数据不是满足高斯分布的，可以变化一下数据，例如log(x+C),x^(1/2)等
• 如果p(x)的值无论异常与否都很大，可以尝试组合多个feature,(因为feature之间可能是有关系的)

5、多元高斯分布

• 单元高斯分布存在的问题
  
  • 如下图，红色的点为异常点，其他的都是正常点（比如CPU和memory的变化）
    
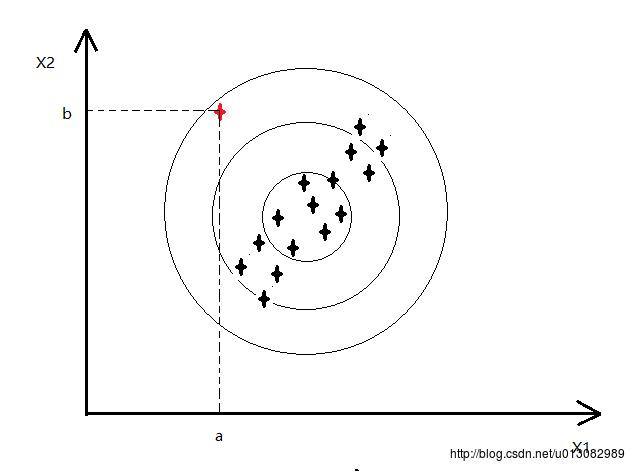
  • x1对应的高斯分布如下：
    
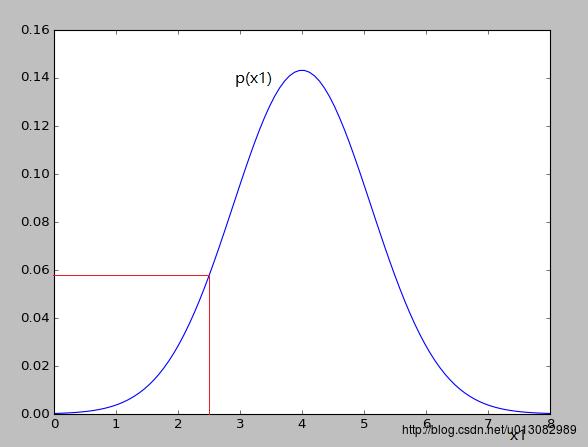
  • x2对应的高斯分布如下：
    
  • 可以看出对应的p(x1)和p(x2)的值变化并不大，就不会认为异常
  • 因为我们认为feature之间是相互独立的，所以如上图是以正圆的方式扩展
• 多元高斯分布
  
  • ，并不是建立p(x1),p(x2)...p(xn)，而是统一建立p(x)
  • 其中参数：,Σ为协方差矩阵
  • 
  • 同样，|Σ|越小，p(x)越尖
  • 例如：
    ，
    表示x1,x2**正相关**，即x1越大，x2也就越大，如下图，也就可以将红色的异常点检查出了
    
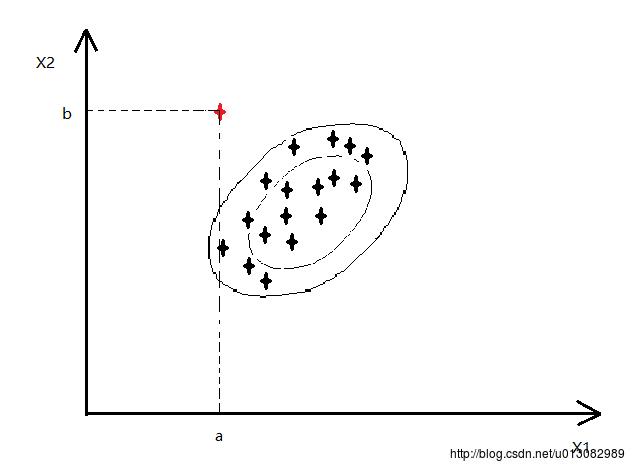
    若：
    ，
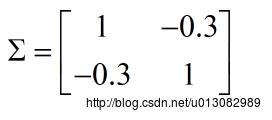    表示x1,x2**负相关**
• 实现代码：

# 多元高斯分布函数    
def multivariateGaussian(X,mu,Sigma2):
    k = len(mu)
    if (Sigma2.shape[0]>1):
        Sigma2 = np.diag(Sigma2)
    '''多元高斯分布函数'''    
    X = X-mu
    argu = (2*np.pi)**(-k/2)*np.linalg.det(Sigma2)**(-0.5)
    p = argu*np.exp(-0.5*np.sum(np.dot(X,np.linalg.inv(Sigma2))*X,axis=1))  # axis表示每行
    return p

6、单元和多元高斯分布特点

• 单元高斯分布
  
  • 人为可以捕捉到feature之间的关系时可以使用
  • 计算量小
• 多元高斯分布
  
  • 自动捕捉到相关的feature
  • 计算量大，因为：
  • m>n或Σ可逆时可以使用。（若不可逆，可能有冗余的x，因为线性相关，不可逆，或者就是m

7、程序运行结果

• 显示数据
  
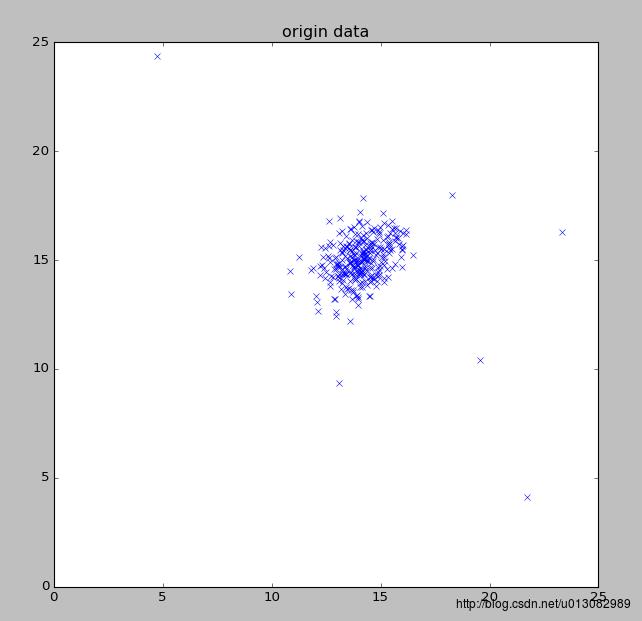
• 等高线
  
• 异常点标注