基于matlab的排队系统仿真

Posted 2022-12-11 fpga和matlab

欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       排队系统是基本的离散事件系统，了解掌握离散事件系统是研究排队系统仿真不可或缺的前提。离散事件系统是指其状态变量只在某些离散时间点上发生变化的系统。这种系统的状态通常只取有限个离散值，对应于系统部件的好坏、忙闲及待处理工件个数等可能的物理状况。而这些状态的变化则由于诸如某些环境条件的出现或消失、系统操作的启动或完成等各种事件的发生而引起。离散事件系统大量地存在于我们的周围，常见的有排队系统、库存管理系统等。利用仿真技术对这些系统进行研究分析，可以了解它们的动态运行规律，从而帮助人们做出最佳的选择或决定。

       排队论最早由A.K.Erlang于1918年提出，随着社会的进步，离散事件系统及排队系统的研究也一直延伸着。在排队系统中，排队愈长就意味着浪费时间愈多，这一系统的效率就愈低，但是盲目地增加服务台也并不一定就能提高效率，因为有可能会使服务空闲时间太多。故对排队问题的分析实质上是一个平衡等待时间和服务台空闲时间的问题，也就是如何确定一个排队系统，能使临时实体和服务台两者都有利，即服务台利用率要高，实体等待时间又不太长。

排队是最基本的离散事件，研究排队系统仿真要先掌握离散事件系统的仿真。离散事件系统是指受事件驱动、系统状态跳跃式变化的动态系统，系统的迁移发生在一串离散事件点上。这种系统往往是随机的，具有复杂的变化关系，难于用常规的微分方程、差分方程等方程模型来描述，仿真技术为解决这类问题提供了有效的手段。描述离散事件系统的基本要素有，实体、事件、活动、进程等。

排队系统（即离散事件系统）仿真研究的一般步骤为：

1. 系统建模:反映实体历经的过程，实体间的作用和逻辑关系；确定随机变量的模型。
2. 确定仿真算法:产生随机变量；确定仿真建模策略。
3. 建立仿真模型:定义状态变量、有关属性、活动及进程、设计仿真钟的推进方法等。
4. 设计仿真程序:仿真语言或高级语言；长期运行或多次运行。
5. 仿真结果分析：统计结果、可信度分析等。

二、核心程序

然后设计一个GUI界面进行运行仿真。

        分别对这几种排队方式下进行仿真，主要对比的仿真波形有三组，然后相关的文献我都已经放在参考文件夹中了。

        目前，用的比较多的都是单队列多服务台，这种模式是效率最高的。具体你可以看看我的PPT。

        另外一方面，单队列和多大队列在理论上差不多，其中区别是单多列可以快速的进入服务台，而多队列，客户在选择服务台的时候，存在着和其他客户之间选择服务台的问题，而且，会导致有些队列人多，有些队列人少的问题。从而影响了最终的排队效率。

function[Blocking_Rate,Use_Rate]=func_mms2(Time_Arrival,Time_Server,Num_queue,Num_People,Num_Server);

%三行依次为：到达时间间隔，服务时间，等待时间
People_State      = zeros(3,round(Num_People/Num_queue)+1);  
%到达时间服从指数分布
People_State(1,:) = exprnd(Time_Arrival,1,round(Num_People/Num_queue)+1);
%服务时间服从指数分布                
People_State(2,:) = exprnd(Time_Server,1,round(Num_People/Num_queue)+1);
%初始化
for i=1:Num_Server
    People_State(3,1:Num_Server)=0;
end
%累积到达时间
Time_Arrival_sum        = cumsum(People_State(1,:));
People_State(1,:)       = Time_Arrival_sum;
%离开时间
Leave_Time(1:Num_Server)= sum(People_State(:,1:Num_Server));     
Server_desk             = Leave_Time(1:Num_Server);
 
for i=(Num_Server+1):round(Num_People/Num_queue)+1
    %当时服务台最早离开的顾客的离开时间减去第i个顾客的到达时间
    if Time_Arrival_sum(i)>min(Server_desk)
       People_State(3,i)=0;                    
    else 
       People_State(3,i)=min(Server_desk)-Time_Arrival_sum(i);     
    end
   Leave_Time(i)=sum(People_State(:,i));
   for j=1:Num_Server 
       if Server_desk(j)==min(Server_desk)
          Server_desk(j)=Leave_Time(i);
          break
       end           
   end
end

Max_time                  = Leave_Time(round(Num_People/Num_queue)+1)*2;
Server_desk(1:Num_Server) = Max_time;
Blocking_Num              = 0;
Blocking_Line             = 0;

for i=1:round(Num_People/Num_queue)+1
    if Blocking_Line==0
       find_max=0;    
       for j=1:Num_Server
           if Server_desk(j)==Max_time
              %服务台有空位
              find_max=1;   
              break
           else
              continue
           end
       end
       if find_max==1
          %更新服务台
          Server_desk(j)=Leave_Time(i);
          for k=1:Num_Server
              if Server_desk(k)<Time_Arrival_sum(i)
                 Server_desk(k)=Max_time;
              else
                 continue
              end
          end
       else
            if Time_Arrival_sum(i)>min(Server_desk)
               %时间间隔T内有人离开
                for k=1:Num_Server
                    if Time_Arrival_sum(i)>Server_desk(k)
                        Server_desk(k)=Leave_Time(i);
                        break
                    else continue
                    end
                end
                for k=1:Num_Server
                    if Time_Arrival_sum(i)>Server_desk(k)
                        Server_desk(k)=Max_time;
                    else continue
                    end
                end
            else
                %时间间隔T内有人离开
                Blocking_Num=Blocking_Num+1;
                Blocking_Line=Blocking_Line+1;
            end
        end
    else
        %队长不为0的情况
        n=0;
        %计算时间间隔T内离开的人数n
        for k=1:Num_Server
            if Time_Arrival_sum(i)>Server_desk(k)
                n=n+1;
                Server_desk(k)=Max_time;
            else continue
            end
        end
        for k=1:Blocking_Line
            if Time_Arrival_sum(i)>Leave_Time(i-k)
                n=n+1;
            else continue
            end
        end
        if n<Blocking_Line+1
            Blocking_Num=Blocking_Num+1;
            for k=0:n-1
                if Leave_Time(i-Blocking_Line+k)>Time_Arrival_sum(i)
                    for m=1:Num_Server
                        if Server_desk(m)==Max_time
                            Server_desk(m)=Leave_Time(i-Blocking_Line+k);
                            break
                        else continue
                        end
                    end
                else
                    continue
                end
            end
            Blocking_Line=Blocking_Line-n+1;
        else
            %更新服务台时间表及队列长度
            for k=0:Blocking_Line
                if Time_Arrival_sum(i)<Leave_Time(i-k)
                    for m=1:Num_Server
                        if Server_desk(m)==Max_time
                            Server_desk(m)=Leave_Time(i-k);
                            break
                        else continue
                        end
                    end
                else
                    continue
                end
            end
            Blocking_Line=0;
        end
    end
end
                                                   
Blocking_Rate = Blocking_Num/(round(Num_People/Num_queue)+1);
Use_Rate      = (round(Num_People/Num_queue)+1)/(Leave_Time(round(Num_People/Num_queue)+1)*(Num_Server/Time_Server));
     

三、测试结果

  ·单队列单服务台

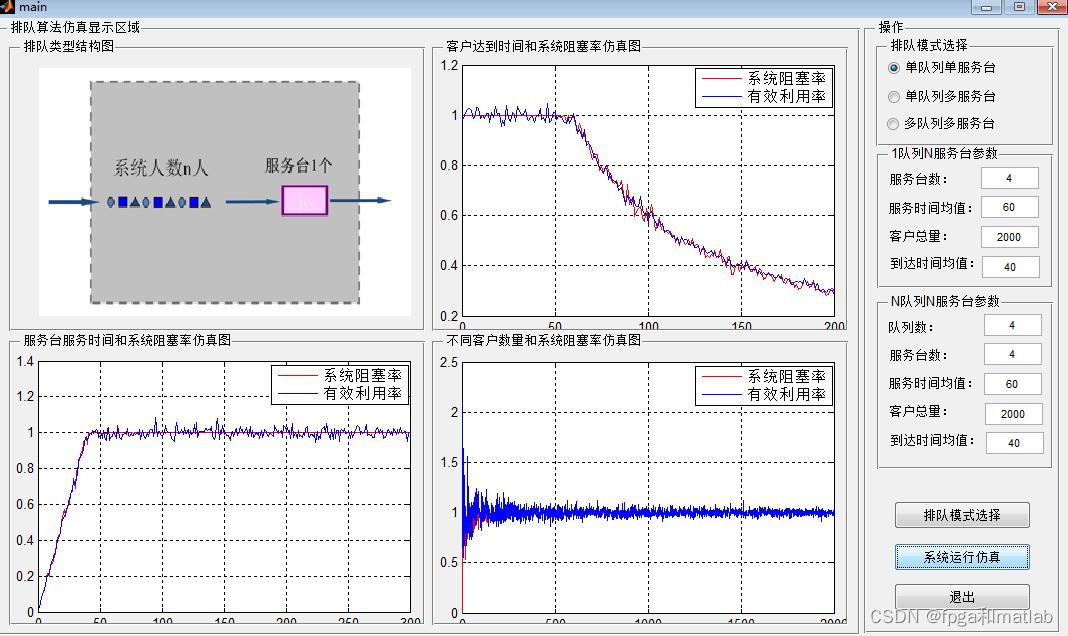
  ·单队列多服务台

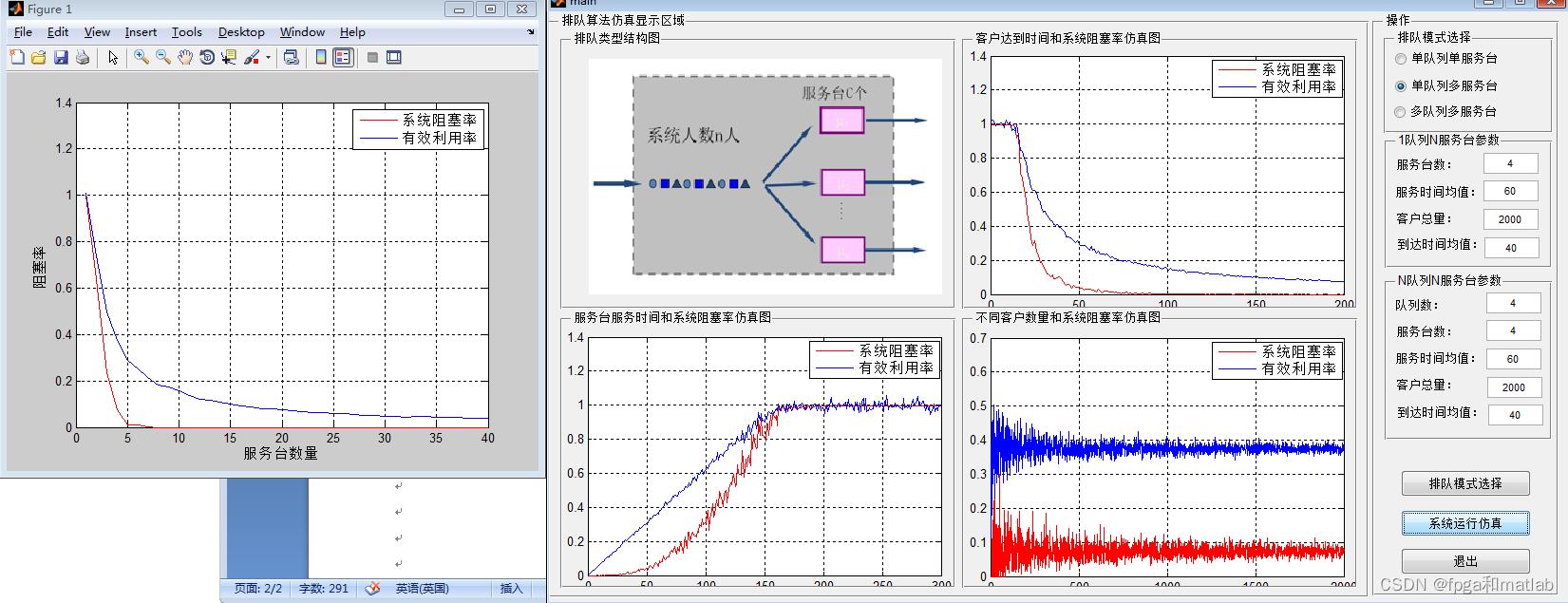
  ·多队列多服务台

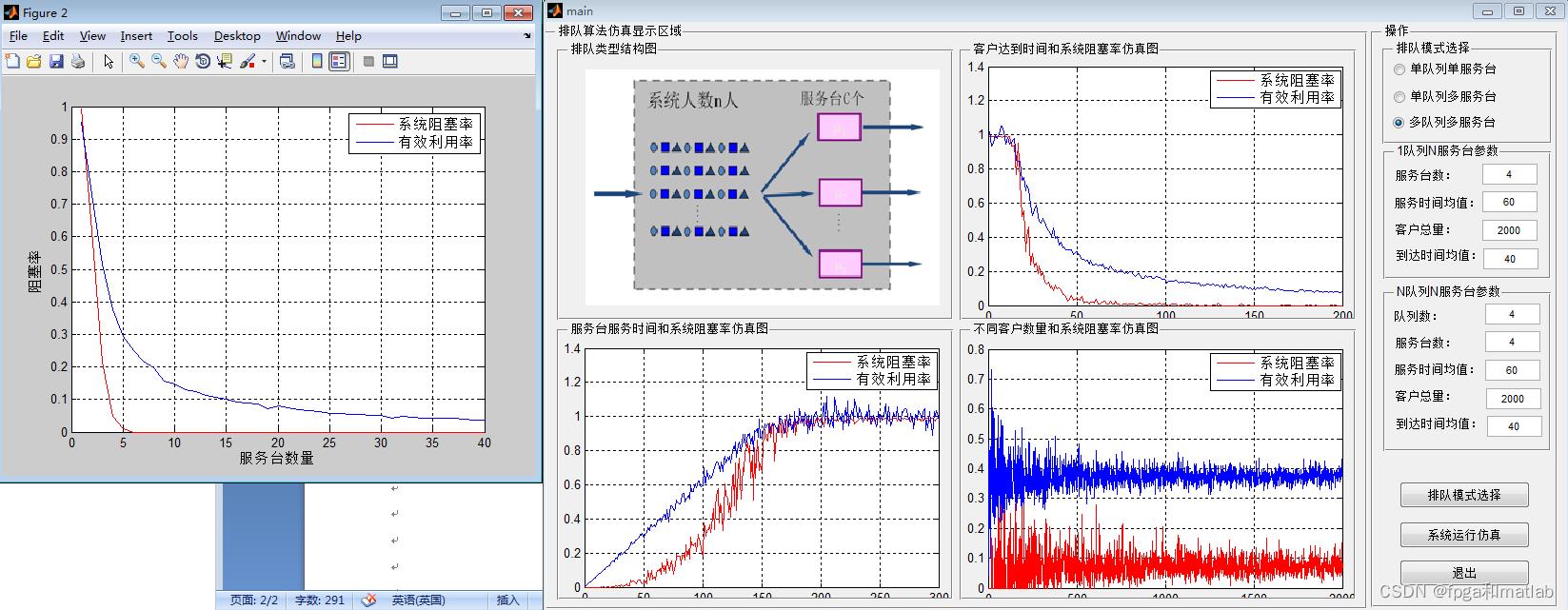
A16-22