机器学习-3.数据特征预处理与数据降维

Posted 2022-12-09 wyply115

• 特征预处理定义：通过特定的统计方法（数学方法）将数据转换成算法要求的数据。
• 处理方法

1. 数值型数据：标准缩放（1.归一化，2.标准化）；缺失值。
2. 类别型数据：one-hot编码。
3. 时间类型：时间的切分。

• 预处理API：sklearn.preprocessing

一、特征预处理

1. 归一化

• 特点：通过对原始数据进行变换把数据映射到（默认为[0,1]）之间
• 公式：
  $$X^{\prime }=\frac{x-min}{max-min}$$
  $$X^{\prime \prime }=X^{\prime }\ast (mx-mi)+mi$$
  注：作用于每一列，max为一列的最大值，min为一列的最小值，那么X’'为最终结果，mx，mi分别为指定区间值（默认mx为1，mi为0）
• 归一化API：sklearn.preprocessing.MinMaxScaler
• 示例：

from sklearn.preprocessing import MinMaxScaler

def minmaxscaler():
    '''
    归一化处理
    :return:None
    '''

    datalist = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
    mms = MinMaxScaler(feature_range=(0, 1))  # feature_range：制定缩放区间，默认为0到1
    data = mms.fit_transform(datalist)
    print(data)

    return None


if __name__ == '__main__':
    minmaxscaler()

• 输出结果为：
  
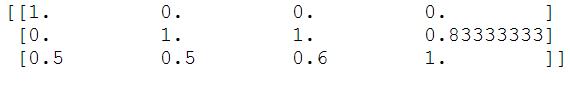
• 为什么要进行归一化处理？
  – 要使得某一个特征对最终结果不会造成更大影响。一般在多个特征对目标值的影响具有同样重要的作用时进行归一化。后期一般会根据算法的要求是否进行归一化，举例：假设有三个特征值，第一个样本是：100，1.2，0.3；第二个样本是 20，1.5，0.35；
  大家都知道方差的公式中包含：（100-20）^2 + (1.2-1.5)^2 + (0.3-0.35)^2。这样第一个特征会非常明显的对目标值具有更大的影响，因此需要进行归一化处理。
• 归一化的缺点：在某些特定场景下，最大值最小值是变化的，另外最大值和最小值非常容易受到异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。
• 鲁棒性定义：是健壮和强壮的意思。它是在异常和危险情况下系统生存的关键。所谓“鲁棒性”，是指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性。

2. 标准化

• 上面提到归一化鲁棒性较差，容易受到异常点的影响，标准化则解决这个问题。
• 特点：通过对原始数据进行变换，把数据变换到均值为0，标准差为1的范围内。
• 公式：
  $$X^{\prime }=\frac{x-mean}{\sigma }$$
• 注：作用于每一列，mean为平均值，σ为标准差
• 假设var为方差，$$var=\frac{(x1-mean{)}^2+(x2-mean{)}^2+....}{n(每个特征的样本数量)}，\sigma =\sqrt{var}$$
• 其中方差是考虑数据的稳定性。
• 对于归一化来讲，如果出现异常点，影响了最大值最小值，那么结果显然改变较大。
• 而对于标准化来讲，如果出现异常点，因为具有一定量的数据，少量的异常点对于平均值的影响不大，因此方差改变较小，最终标准化改变也较小，因此大部分是采用标准化。
• API：sklearn.preprocessing.StandardScaler
• 示例：

from sklearn.preprocessing import StandardScaler

def standscaler():
    '''
    标准化处理
    :return: None
    '''

    datalist = [[1,-1,3],[2,4,2],[4,6,-1]]
    stand = StandardScaler()
    data = stand.fit_transform(datalist)
    print(data)
    return None

if __name__ == '__main__':
    standscaler()

• 输出结果为：
  
• 标准化总结：在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

3. 缺失值

• 缺失值的处理：

1. 删除：如果每列或者行数据缺失值达到一定的比例，建议放弃整行或者整列。
2. 插补：可以通过缺失值每行或者每列的平均值、中位数来填充。

• API：sklearn.preprocessing.imputer
• 示例：

from sklearn.preprocessing import Imputer
import numpy as np

def im():
    '''
    缺失值处理
    :return:None
    '''
    datalist = [[1,2],[np.nan,3],[7,6]]
    im = Imputer(missing_values='NaN',strategy='mean',axis=0)
    data = im.fit_transform(datalist)
    print(data)

    return None

if __name__ == '__main__':
    im()

• 输出结果如下：
  

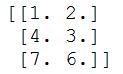
二、数据降维

• 降维，维度：指特征的数量
• 通俗来讲，就是因为有的特征对目标值的预测没有意义或者部分特征的相关度高，容易消耗计算性能，所以需要特征的选择，也就是数据降维。
• 特征选择主要方法（三大武器）：

1. Filter(过滤式)：VarianceThreshold(是通过计算方差进行的过滤，当存在很多个特征值时，通过计算方差来分析每一个特征值是否能很好的体现区分度，如果方差很小或者是0，那么这样的特征值就不存在分析的价值了，一般可以用作预处理当中)
2. Embedded(嵌入式)：正则化、决策树
3. Wrapper(包裹式)：不常用

• 映射方法（三大类）

1. 线性映射方法：PCA(主成份分析)、LDA(线性判别分析，不常用)等
2. 非线性映射方法：核方法：KPCA、KFDA等；二维化；流形学习：ISOMap、LLE、LPP等。
3. 其他方法：神经网络和聚类

1. 特征选择-过滤式

• VarianceThreshold的API：sklearn.feature_selection.VarianceThreshold
• 示例：

from sklearn.feature_selection import VarianceThreshold

def var():
    '''
    特征选择-过滤式-过滤掉低方差的特征
    :return: None
    '''
    datalist = [[0,2,0,3],[0,1,4,3],[0,1,1,3]]
    var = VarianceThreshold(threshold=0.0) # threshold指定阀值方差,指定1时则小于等于1的方差特征都会删除
    data = var.fit_transform(datalist)
    print(data)

    return None


if __name__ == '__main__':
    var()

• 输出结果为：
  
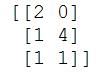
  由结果看出，第一个特征和第四个特征，方差均为0，因此被删除掉了。

2. 映射方法-PCA(主成份分析)

• API：sklearn.decomposition
• 本质：PCA是一种分析、简化数据集的技术
• 目的：使数据压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
• 作用：可以消减回归分析或者聚类分析中特征的数量。
• 通过一个例子来说明何为主成份分析：
  

1. 如上图所示，如何对一个立体物体进行二维表示
2. 第一张图明显看不出是个什么东西，第二张图也一样，第三张图勉强能够看出是个洒水壶但不明显，第四张图一眼就能看出来了。主成份分析就是如何通过低纬度表示出高纬度的数据并且主要特征都不缺失。因此一般我们当特征数量上百时会考虑数据的简化，进行PCA操作，如果特征只有几个或几十个一般是没有必要去进行PCA操作的。PCA操作即会把数据改变，也会降低特征数量。

• 简易示例：

from sklearn.decomposition import PCA

def pca():
    '''
    主成份分析进行数据降维
    :return: None
    '''

    datalist = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]
    pca = PCA(n_components=0.9) # n_components:可以是小数 0-1，小数代表数据保留百分之多少，根据经验一般在90%-95%；可以是整数（一般不用），代表减少到的特征数量
    data = pca.fit_transform(datalist)
    print(data)

    return None


if __name__ == '__main__':
    pca()

• 输出结果如下：
  
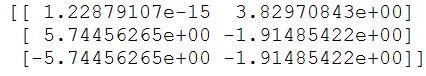
  如上图所示，通过pca处理，将原有的四个特征，在制定保留90%数据时，降维到两个特征。

3. 特征选择与主成份分析如何选择

• 一般特征数量较多（过百）时采用主成份分析，较少时采用特征选择

4. 小结

• 至此，特征工程三块知识点：1. 特征抽取；2. 特征预处理；3. 数据降维。已经总结完毕，后期再穿插更深入的内容。