R语言一张表解释正态分布函数（dnorm pnorm qnorm rnorm z分数）

Posted 2022-12-08 基督徒Isaac

参考文献：https://zhuanlan.zhihu.com/p/108514652

解释：

library(tidyverse)

# R统计学(08): 正态分布 (一)  辉小宝同学 R语言和Python学堂----
# https://mp.weixin.qq.com/s?__biz=Mzg5MjAyMTk2Mg==&mid=2247484891&idx=1&sn=daac84e9aefea11020b410afbc2d274d&chksm=cfc5387ef8b2b1681fc23d5668a64b4a014c7993de27af257b7968f09af9feceb19d4ab02bab&scene=21#wechat_redirect
win.graph()
par(mfrow = c(4, 4))
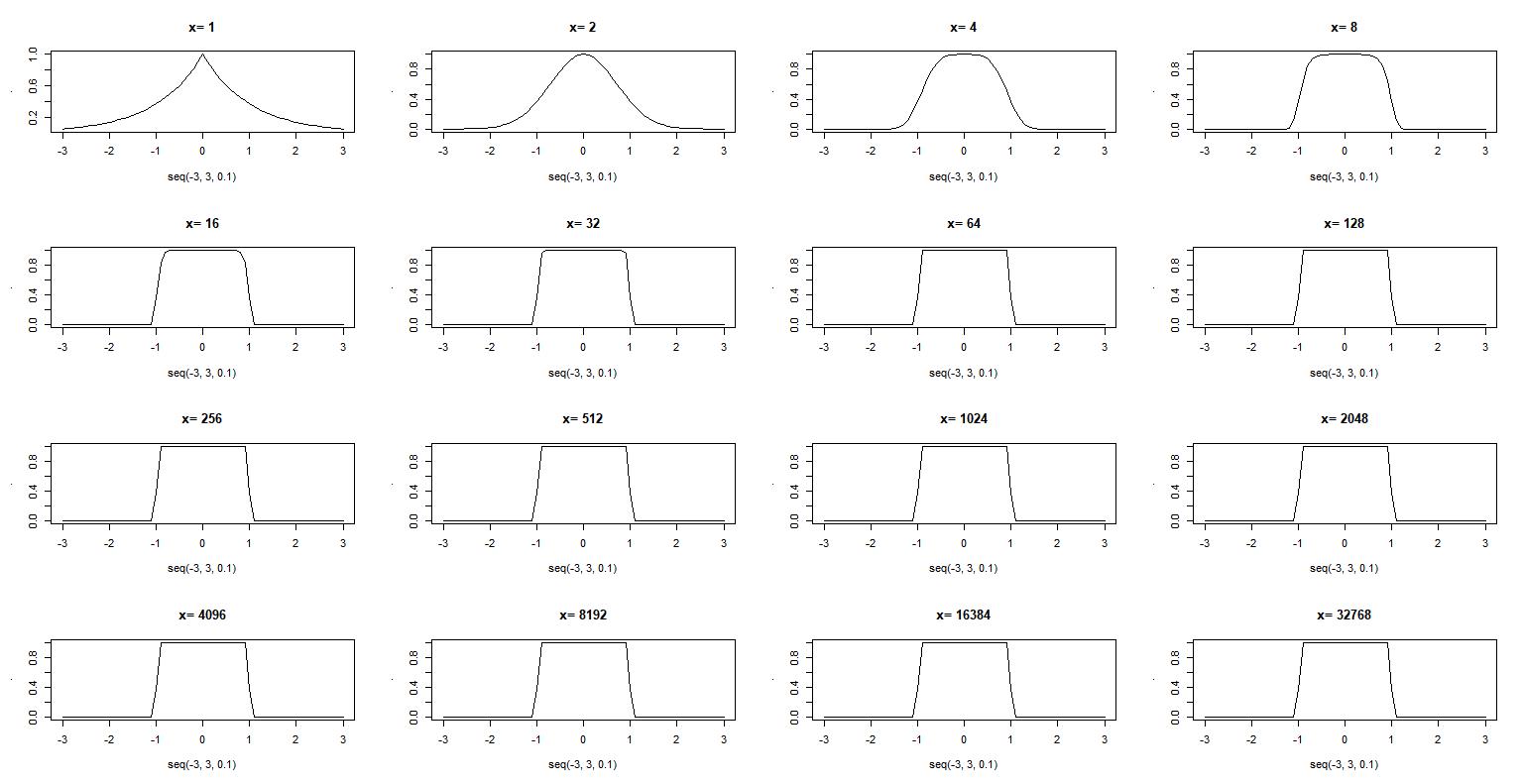
for (i in 2**c(0:15)) 
  exp(-abs(seq(-3,3,0.1))**i) %>% 
    plot(x = seq(-3,3,0.1), y = ., type = "l", main = paste("x=", i))


win.graph()
par(mfrow = c(2, 2))
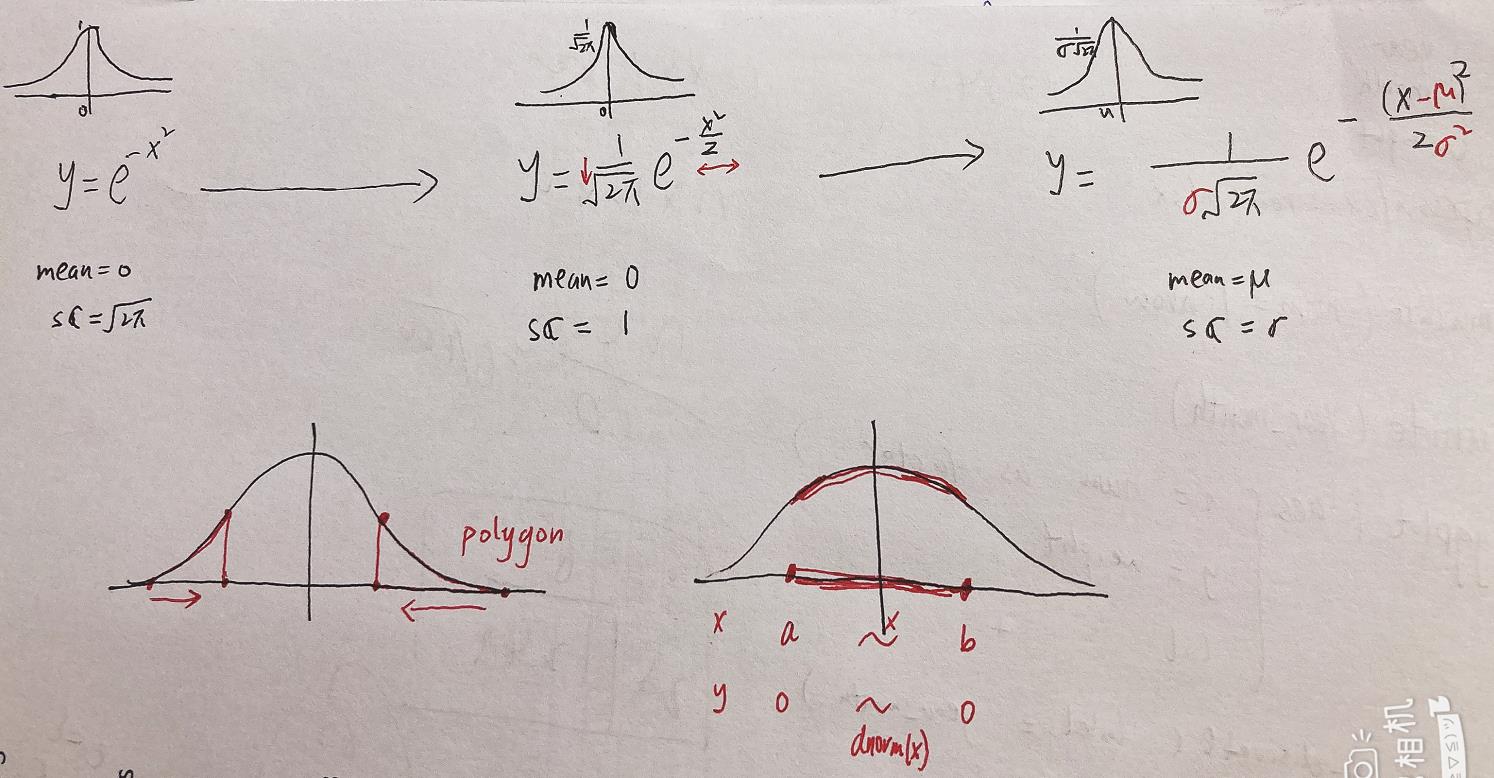
for (i in c(1/4, 1/2, 2, 4)) 
  exp(-seq(-3,3,0.1)**2) %>% 
    plot(x = seq(-3,3,0.1), y = ., type = "l")
  lines(x = seq(-3,3,0.1),
        y = dnorm(seq(-3,3,0.1)), col = 2);
  lines(x = seq(-3,3,0.1),
        y = dnorm(seq(-3,3,0.1), 0, i), col = 3)
  title(main = paste("u= 0, sigma=", i))


# 假设我们测量了 100个人的身高。平均身高为 170厘米，标准偏差为 8厘米----

# 身高小于 160厘米的概率
pnorm(160, mean = 170, sd = 8) ==
  pnorm((160-170)/8)
# 身高大于 185厘米的概率
1 - pnorm(185, mean = 170, sd = 8) ==
  1- pnorm((185-170)/8)
# 身高在 160厘米至 185厘米之间的概率 == 身高大于 160厘米且小于 185厘米的概率
pnorm(185, mean = 170, sd = 8) - pnorm((160-170)/8) ==
  pnorm((185-170)/8) - pnorm((160-170)/8)

# 画图
# https://vimsky.com/examples/usage/draw-a-polygon-between-specified-points-in-r-programming-polygon-function.html
win.graph()
par(mfrow = c(3, 2))
# 身高小于 160厘米的概率
u <- 170; s <- 8; x <- 160; z <- (x-u)/s; z
plot(x = seq(u-3*s, u+3*s, 0.01),
     y = dnorm(seq(u-3*s, u+3*s, 0.01), u, s),
     type = "l", xlab = "身高", ylab = "概率密度",
     main = paste("N ~ (", u, ",", s**2, ")", sep = ""))
polygon(x = c(seq(u-3*s, x, 0.01), x, u-3*s),
        y = c(dnorm(seq(u-3*s, x, 0.01), u, s), 0, 0), col = 2)
plot(x = seq(-3, 3, 0.01),
     y = dnorm(seq(-3, 3, 0.01)),
     type = "l", xlab = "身高", ylab = "概率密度",
     main = paste("N ~ (", 0, ",", 1, ")", sep = ""))
polygon(x = c(seq(-3, z, 0.01), z, -3),
        y = c(dnorm(seq(-3, z, 0.01)), 0, 0), col = 2)

# 身高大于 185厘米的概率
x <- 185; z <- (x-u)/s; z
plot(x = seq(u-3*s, u+3*s, 0.01),
     y = dnorm(seq(u-3*s, u+3*s, 0.01), u, s),
     type = "l", xlab = "身高", ylab = "概率密度",
     main = paste("N ~ (", u, ",", s**2, ")", sep = ""))
polygon(x = c(seq(x, u+3*s, 0.01),  u+3*s, x),
        y = c(dnorm(seq(x, u+3*s, 0.01), u, s), 0, 0), col = 2)
plot(x = seq(-3, 3, 0.01),
     y = dnorm(seq(-3, 3, 0.01)),
     type = "l", xlab = "身高", ylab = "概率密度",
     main = paste("N ~ (", 0, ",", 1, ")", sep = ""))
polygon(x = c(seq(z, 3, 0.01), 3, z),
        y = c(dnorm(seq(z, 3, 0.01)), 0, 0), col = 2)

# 身高在 160厘米至 185厘米之间的概率 == 身高大于 160厘米且小于 180厘米的概率
# 左边距离平均值相差-1.25个标准差，右边距离平均值相差1.875个标准差
plot(x = seq(u-3*s, u+3*s, 0.01),
     y = dnorm(seq(u-3*s, u+3*s, 0.01), u, s),
     type = "l", xlab = "身高", ylab = "概率密度",
     main = paste("N ~ (", u, ",", s**2, ")", sep = ""))
polygon(x = c(160, seq(160, 185, 0.01), 185),
        y = c(0, dnorm(seq(160, 185, 0.01), u, s), 0), 
        col = "darkgreen", border = "red", lwd = 2)
plot(x = seq(-3, 3, 0.01),
     y = dnorm(seq(-3, 3, 0.01)),
     type = "l", xlab = "身高", ylab = "概率密度",
     main = paste("N ~ (", 0, ",", 1, ")", sep = ""))
polygon(x = c(-1.25, seq(-1.25, 1.875, 0.01), 1.875),
        y = c(0, dnorm(seq(-1.25, 1.875, 0.01)), 0), 
        col = "darkgreen", border = "red", lwd = 2)