联邦学习——基于聚类抽样进行客户选择

Posted 2022-12-08 联邦学习小白

《Clustered Sampling: Low-Variance and Improved Representativity for Clients Selection in Federated Learning》针对目前联邦学习中的节点选择策略存在的有偏抽样、server-client通信和训练稳定性问题，这篇文章提出采用聚类抽样的方法进行节点选择，并证明了聚类抽样能提高用户的代表性、减少不同客户聚合时的权重方差。本文提出了基于样本数量和基于相似性的两种聚合抽样方法，并通过实验证明，采用聚类抽样的方法进行节点选择可以使聚合模型在训练和测试时取得更快更平滑的收敛性。

无偏抽样

当抽样得到的客户聚合的期望值等于考虑所有客户而得到的全局聚合时，这样的客户抽样方案称为无偏抽样方案。
看文字可能不太好来理解，用公式表达就是(6)的形式，其中 $w_j(S_t)$ 是抽样得到的客户子集 $S_t$ 中客户 j 的聚合权重，$p_i$是客户 i 的样本数量$n_i$ 在所有客户的样本数量 M = ${\Sigma }_{i=1}^n{n}_i$ 中的比例$n_i$/M，也是所有客户聚合时，客户 i 的聚合权重。

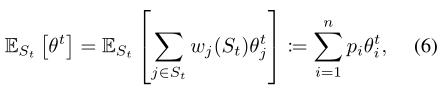
一、节点选择策略

文章提到，目前大多数的节点选择策略都需要额外的server-clients通信代价，且无法实现无偏抽样。作者的观点是，FedAvg和MD抽样是仅有的能保持最小server-clients通信代价的节点选择策略。

1、FedAvg

我们知道FedAvg算法在每轮聚合时都只选择部分节点进行聚合，但它的选择方式是随机的，这将导致有偏抽样，且一些具有独特数据分布的客户可能难以被选中，进而影响全局模型的收敛。

2、MD抽样

multinomial distribution(MD)抽样的节点选择概率与该节点的相对样本数量（样本数量在所有客户样本数量中的比例）相关。实验证明，MD抽样的表现优于FedAvg，且可实现无偏抽样。
文章提到“据我们所知，FedAvg和MD抽样是保持最小sever-client通信的唯一方案。并且MD抽样已经被证明可以使FL达到最佳状态”
但MD抽样在节点选择过程中仍存在较大的差异，具体来讲，比如抽样m次，MD中客户被抽中的次数为0-m，这可能使每一轮参与聚合的客户的数据分布与上一轮的存在巨大差异，且一些客户可能从头到尾未被抽到，进而降低了一些客户的代表性，并使全局模型的收敛存在较大的不稳定性。

3、聚类抽样

聚类抽样是一种对MD抽样进行改进的新的无偏客户抽样方案，在保持最小的sever-clients通信代价的基础上，保证更小的节点选择差异性。同时为提高模型聚合时每个客户的代表性，聚类抽样保证了那些具有独特数据分布的客户可以被选中，从而实现更平滑、更快速的全局模型收敛。
聚类抽样和MD抽样的不同在于，MD根据相同的客户分布$w_0$抽样m次，以获得m个客户并根据客户的相对样本数量进行全局聚合，聚类抽样则是根据m个客户分布$w_k(t)$${}_{k=1}^m$，每个分布抽样一次，获得m个客户并以 “客户 i 的样本数量在该分布$w_k(t)$中的比例” $r_{k,i}^t$作为聚合权重参与第 t 轮全局聚合。

二、聚类抽样的无偏性和收敛性分析

1、聚类抽样的无偏性

由聚类抽样的的定义便有式(7)

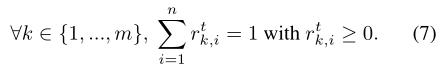
将无偏抽样的概念扩展至m个独立抽样分布$w_k(t)$${}_{k=1}^m$，便有

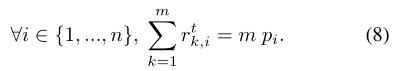
文章进而提出命题1并加以证明：只要一个聚类抽样满足式(7)和式(8)，便可实现无偏抽样。

2、MD抽样的收敛边界

聚类抽样是在MD的基础上进行优化的，文章证明了聚类抽样在实现更小的聚合权重、更高的客户代表性的同时，能实现无偏抽样，且具有与DM相同的收敛边界。
关于MD的收敛性分析我就直接贴原文了，其中三个假设都是SGD分析和联邦优化常用的，基于这些假设证明了MD的收敛边界。

3、聚类抽样的收敛边界

文章进一步证明，采用聚类抽样进行节点选择的FedAvg只要满足假设1-3和命题1，就可以实现与采用MD抽样进行节点选择的FedAvg相同的收敛边界。并且，聚类抽样还能实现更快更平滑的收敛。后续实验证明，面对IID数据时，聚类抽样和MD几乎收敛于同一最小值，而面对Non-IID时，聚类抽样则可以收敛至更小值。

四、聚类抽样相对于MD抽样的优点

1. 聚类抽样不仅可以实现和MD抽样相同的收敛边界，还能实现更平滑更快的收敛，在Non-IID情况下，聚类抽样实际上能收敛至更小值
2. 聚类抽样可以减少客户的聚合权重方差。
3. 使用聚类抽样，每个客户被抽样的概率更高，因此在整个FL过程中得到更好的代表性。增加客户代表性可确保具有独特分布的客户更有可能被抽中，并可能实现更平滑和更快的FL收敛。

这些改进对于具有异构联邦数据集的FL应用非常重要。

五、两种聚类抽样算法

满足命题1的聚类抽样算法有很多，文章提出了两种算法，分别是“基于样本数量”和“基于模型相似度”的聚类抽样。

1、 基于样本数量的聚类抽样

得结合Algorithm 1 和 Figure 3来理解。
其实很简单，主要分四步：

1. 每个客户的样本数量为$n_i$，但实际参与计算的每个客户的样本数量定义为$n_i$’ = m$n_i$，m是独立分布的个数。（当然m$n_i$只是用于计算，并不是真的对客户的本地样本进行扩展。）
2. 定义m个独立分布$w_k(t)$${}_{k=1}^m$，每个分布有M个样本，M=${\Sigma }_{i=1}^n$m$n_i$
3. 按顺序将每个客户的样本放入m个分布，多的就放到下一个，也就是Figure 3那样。
4. 根据客户在每个分布中的样本数量定义其在该分布中被抽样的概率
5. 每个分布抽一个客户，共抽样m个客户。

2、优点

• 文章证明了通过Algorithm 1 进行抽样，相比于MD中每个客户最多能被抽样m次，聚类抽样中每个客户被抽中的次数最高为ceil(m$p_i$)+2，这能提高客户的代表性并降低节点选择的差异性（被抽样的次数相差不大）。
• 并且这一抽样方案是符合命题1的，也就是说，Algorithm 1 是无偏抽样。
  
  

2、 基于相似性的聚类抽样

相似性的定义：文章中提出的相似性是基于“代表性梯度”的，“代表性梯度”就是客户的本地模型和全局模型的差异。
这个算法与“基于样本数量”的聚类抽样很像，只不过“基于相似性”的聚类抽样允许聚类数量K可以不等于分布个数m。同样得结合Algorith 2 和Figure 4进行理解。
当k=m时，就可以应用和算法1的相同推理。
当k>m时，就考虑对多出来的k-m个聚类进行重新分配。
具体可以分为以下几步：

1. 首先计算每个客户的“代表性梯度”，根据“代表性梯度”，通过层次聚类将客户聚成k个类，且k≥m。（关于客户数据量的定义和算法1一样）
2. 聚类结果为$B_k$${}_{k=1}^K$，按每个类的样本数量$q_k$对聚类结果进行降序排序。（$q_k$≤M）
3. 将前m个类分别置于m个分布
4. 剩下的k-m个类依次填充这m个分布
5. 根据客户在每个分布中的样本数量定义其在该分布中被抽样的概率
6. 每个分布抽一个客户，共抽样m个客户。

优点

• 由于分布是由“代表性梯度”产生的相似树获得的，因此该方案基于客户的相似度提升了客户的代表性。
• 算法2不需要共享客户的梯度，只需要共享“代表性梯度”，这在实现和标准FL相同的通信代价的同时，保证了客户的隐私。
• 可以采用任何层次聚类算法进行聚类。
• 即使是在有大量客户的情况下，算法2的时间复杂度问题也不大。因为在聚合了新的全局模型之后，服务器可以对客户进行抽样，并将全局模型传给客户。在等待本地训练完成的同时，服务器可以预估新的划分（把每个聚类放入各分布中）。
• 当每个客户的样本量占比$p_i$ = $n_i$ /M ≤1/m时，这一抽样方案是符合命题1的，也就是说，Algorithm 2 是无偏抽样。

四、实验

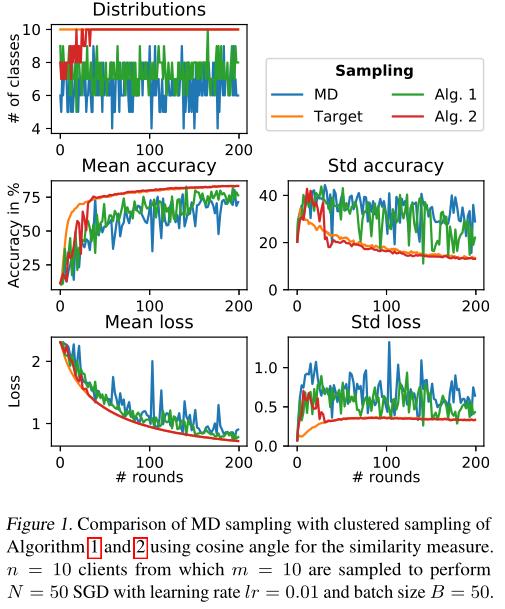
1、 IID情况下

对比MD、Algorithm 1、Algorithm 2、Target四种抽样方案，其中Target是聚类抽样的一种理想情况，需要提前获得客户的数据分布，所以在实际应用中并不可行，但可以作为一种对算法的优化目标。
数据集：MNIST
客户端设计：共100个客户，每个客户有500train，100test，这600条样本为同一个数字，且每个数字分配给10个用户，也就是100个客户可以聚成10个类。

2、Non-IID情况下

对比MD、Algorithm 1、Algorithm 2
数据集：CIFAR10
客户端设计：采用迪利克雷分布(a越小，异构性越强)对CIFAR10进行划分并分配给100个客户，其中10，30，30，20，10个客户分别具备100、250、500、750、1000条训练数据和20、50、100、150、200条测试数据（训练数据的1/5）。

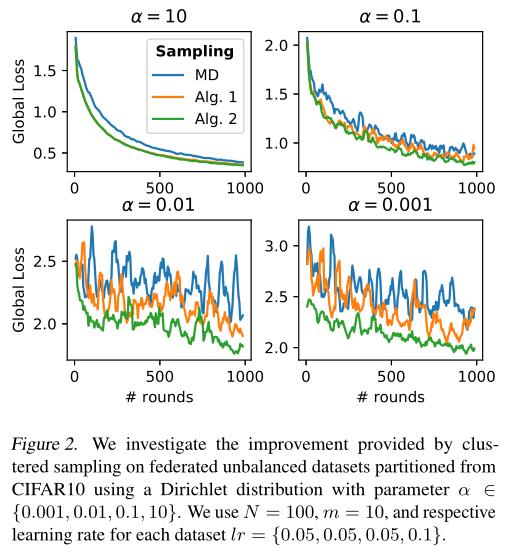
五、总结

Algorithm 1和Algorithm 2都能实现更小的权重方差，并以此提高了客户的代表性。并通过实验证明两个算法都可以在Non-IID数据集下实现更快更平稳的收敛性质。