复杂度计算
Posted oliveQ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了复杂度计算相关的知识,希望对你有一定的参考价值。
复杂度计算和线性代数补充
矩阵结构和算法复杂度
-
定义Flop Count
- 浮点运算(浮点运算):两个浮点数的一个加法、减法、乘法或除法。
- 估计算法的复杂性:将flop数表示为问题维数的(多项式)函数,并通过只保留前导项
- 不是计算时间的准确预测器,支持读写,并行计算
- 是近似估计
-
举例
- x , y ∈ R n , x T y = ∑ i x i y i ⟹ n + ( n − 1 ) = 2 n − 1 ⟺ O ( n ) x,y\\isin R^n,x^Ty=\\sum_ix_iy_i\\implies n+(n-1)=2n-1\\iff O(n) x,y∈Rn,xTy=∑ixiyi⟹n+(n−1)=2n−1⟺O(n)
- A ∈ R m × n , x ∈ R n , A x ⟹ m ( 2 n − 1 ) ⟺ O ( m n ) = m = n O ( n 2 ) A\\isin R^m\\times n,x\\isin R^n,Ax\\implies m(2n-1) \\iff O(mn)\\xlongequalm=n O(n^2) A∈Rm×n,x∈Rn,Ax⟹m(2n−1)⟺O(mn)m=nO(n2)
- A ∈ R m × n , B ∈ R n × p , A B ⟹ m p ( 2 n − 1 ) ⟺ O ( m n p ) = m = n = p O ( n 3 ) A\\isin R^m\\times n,B\\isin R^n\\times p,AB\\implies mp(2n-1) \\iff O(mnp)\\xlongequalm=n=p O(n^3) A∈Rm×n,B∈Rn×p,AB⟹mp(2n−1)⟺O(mnp)m=n=pO(n3)
当A是稀疏,Banded,Toeplitz等状态下可以被分解,简化复杂度。
-
特例:线性等式【Ax=b】
-
A是对角阵, O ( n ) O(n) O(n)
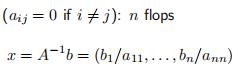
-
A是下三角阵, O ( n 2 ) O(n^2) O(n2)

-
A是正交矩阵orthogonal matrices, O ( n 2 ) O(n^2) O(n2)

-
A是置换(全错排)矩阵permutation matrices, O ( 0 ) O(0) O(0)

-
用分解矩阵求解线性方程Ax=b
- 矩阵A可以由一些简单的矩阵组合得到, A = A 1 A 2 . . . A k , A i A=A_1A_2...A_k,A_i A=A1A2...Ak,Ai可能是对角矩阵,上三角矩阵等
- 求解x可以通过传递求解k个简单的等式
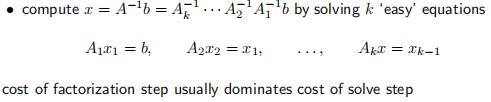
- 整个x向量有m个未知数待求

简化Ax=b求解的复杂度
LU分解–A是非奇异矩阵
-
简单得说就是先用矩阵L做消元,然后再左乘 L − 1 L^-1 L−1。
比如
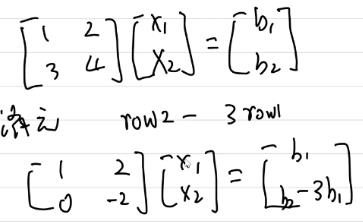
-
于是L矩阵就是 [ 1 0 − 3 1 ] , A = L − 1 L A = L ′ U ′ \\beginbmatrix 1 & 0 \\\\ -3 & 1 \\endbmatrix,A=L^-1LA=L'U' [1−301],A=L−1LA=L′U′
注 : L ′ = L − 1 , U ′ = L A = [ 1 2 0 − 2 ] 注:L'=L^-1,U'=LA=\\beginbmatrix 1 & 2 \\\\ 0 & -2 \\endbmatrix 注:L′=L−1,U′=LA=[102−2]
-
对于需要多步消元的矩阵A,可以转化为 A = L 1 − 1 . . . L n − 1 − 1 ⏟ 下三角矩阵 L n − 1 . . . L 1 A ⏟ 上三角矩阵 = L ′ U ′ A=\\underbraceL_1^-1...L_n-1^-1_\\text下三角矩阵\\underbraceL_n-1...L_1A_\\text上三角矩阵=L'U' A=下三角矩阵 L1−1...Ln−1−1上三角矩阵 Ln−1...L1A=L′U′
-
计算复杂度:每一k行都需要相乘和相加,于是第k行的flop=2(n-k+1)(n-k)
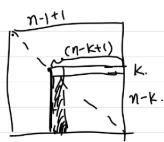
F l o p C o u n t = ∑ k = 1 n − 1 2 ( n − k + 1 ) ( n − k ) Flop Count=\\sum_k=1^n-12(n-k+1)(n-k) FlopCount=∑k=1n−12(n−k+1)(n−k)
= 2 ∑ k = 1 n − 1 ( n − k ) 2 + ∑ ( n − k ) ⏟ 可忽略 =2\\sum_k=1^n-1(n-k)^2+\\underbrace\\sum(n-k)_\\text可忽略 =2∑k=1n−1(n−k)2+可忽略以上是关于复杂度计算的主要内容,如果未能解决你的问题,请参考以下文章