数字图像处理2021期末复习考试重点大纲
Posted Rose J
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字图像处理2021期末复习考试重点大纲相关的知识,希望对你有一定的参考价值。
本文目录
数字图像处理期末复习
1.填空(每空2分,共20分)
1.均值滤波计算

均值滤波方法是,对待处理的当前像素,选择一个模板,该模板为其近邻的若干像素组成,用模板中像素的均值来替代原像素的方法。
如上图所示,序号为0的是当前像素,序号为1~8的像素是其模板中的近邻像素,求模板中所有像素的均值,再把该均值赋予当前像素点(x,y),作为处理后图像在该点上的灰度g(x,y).
公式如下:
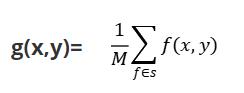
其中,s为模板,M为该模板中包含当前像素在内的像素总个数。
下面,以一个简单的例子来体会均值滤波算法。设检测图像数据(包含噪声干扰)为:

用3 x 3的模板对其进行均值滤波,因为图像画面边框上的像素无法被模板覆盖,因此一般不做处理。对于图像中每一个非边框区域中的像素以其为中心取 3 x 3的邻域,计算9个像素的灰度值均值,并用此均值替代中心像素的灰度值,例如,原图中的像素分f(2,2)=10,从数值上分析,该点的灰度值比其他周围像素的灰度值大,所以可初步判断其为噪声点。
覆盖该点的模板为:
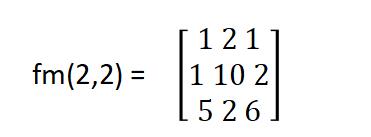
则滤波后的结果为
g(2,2)=int(1/9 x (1+2+1+1+10+2+5+2+6))=3
int表示取整函数,即将像素值大于周围像素的噪声进行了很好的抑制。
同理,对原图中的像素f(4,4),其模板中的像素为

则滤波后的结果为
g(4,4)=int(1/9 x (6+868+7+0+8+7+8+9))=7
即将像素值小于周围像素的噪声进行了很好的抑制。最终,对原图进行处理后的结果图像为
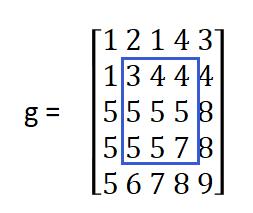
(嘘~其实就是求这9个点里的平均数)
2.中值滤波计算
取某种结构的二维滑动模板,将模板内像素按照像素值的大小进行排序,生成单调上升(或下降)的二维数据序列,类似一维,二维中值滤波输出为
公式如下:
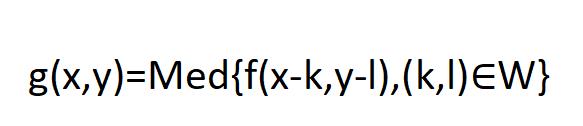
其中,f(x,y),g(x,y)分别为原图像和处理后图像,W为二维模板,通常选为3 x 3,
5 x 5区域,也可以有不同的形状,如线状,圆形,十字行,圆环形等
下面,以一个简单的例子来体会中值滤波算法。设检测图像数据(包含噪声干扰)为:
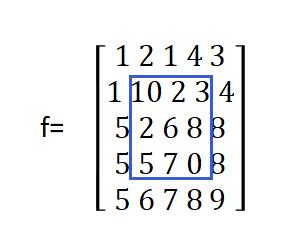
用3 x 3的模板对其进行中值滤波,同样因为图像画面边框上的像素无法被模板覆盖,一般不做处理,对于每一个非边框区域中的像素,以其为中心取3 x 3的邻域,对该领域中9个像素的灰度值进行递增排序,并用其中值替代中心像素的灰度值。
例如:
原图中的像素f(2,2),其模板中的像素为

对模板中的9个数从小到大排序为1,1,1,2,2,2,5,6,10,则滤波后的结果为排在该数据序列中间位置,即g(2,2)=2,即将像素值大于周围像素的噪声进行了很好的抑制,
同理,对原图中的像素f(4,4),其模板中的像素为
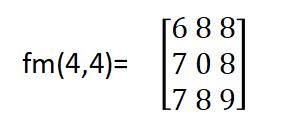
数据排序后0,6,7,7,8,8.8,8,9,则滤波后的结果为g(4,4)=8,即将像素值小于周围像素的噪声进行了很好的一直。最终,对原图进行处理后的结果图像为

(其实就是这段数据中的中位数)
3.水平方向一阶锐化计算
水平方向的微分算子就是要获得推向在水平方向上的变化率。水平微分算子定义如下:

按照图像处理的模板描述形式,上式可以表示为
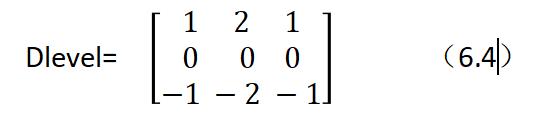
其中,待处理像素位于模板的中心
例:
下面以一个简单的例子来体会该算法,设原图像为:
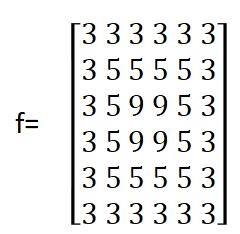
对f中模板罩不住的地方其处理结果令为0,其他的像素一次按照式(6.4)进行计算。
例如:
对f(2,3),3x3的模板下的图像子块为
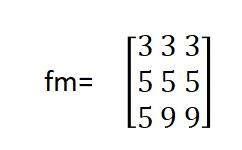
计算结果为:
g(2,3)=(3-5)+2(3-9)+(3-9)=-20
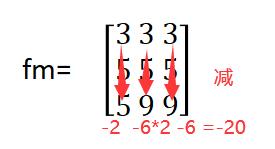
最终可得处理结果为

为了显示结果图像,最后需要将图像数据进行标准化,即通过一个简单的线性映射将【gmin,gmax】映射到【0,255】。这里,对g的所有元素都进行+20处理,有

(其实就是那个数 上面的数 ** 减去 下面的数** 的和)
4.无方向一阶锐化计算
1.交叉微分算法(Roberts算法)计算公式如下:
g(i,j)=|f(i+1,j+1)-f(i,j)|+|f(i+1,j)- f(i,j+1)|


就是交叉减法的绝对值和
2.Sobel锐化的计算公式如下:


3.Priwitt锐化算法的计算公式如下:
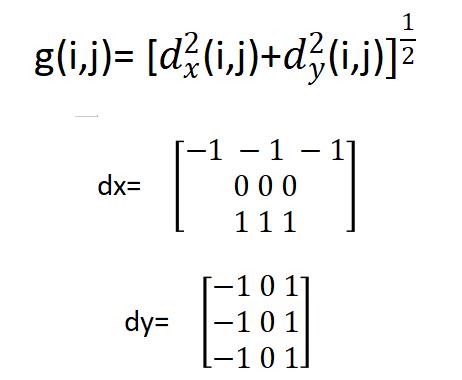

5.位图文件存储所需要的数据量计算
用字节表示文件大小时,一张未经压缩的数字图像的数据量大小计算如下:
图像数据量大小=像素总数 x 图像深度/8(单位:字节)
,例如:一幅画的尺寸是 1024*768, 深度为16,则它的数据量为1.5M。
计算如下:
1024 * 768 * 16bit
= (1024 * 768 * 16) / 8 byte
= [(1024 * 768 * 16) / 8] / 1024KB
= [(1024 * 768 * 16) / 8] / 1024 / 1024MB。

灰度图像深度 8
彩色图像深度 24
2.问答(每题10分,共10分)
1、什么是采样,简述采样间隔与图像的关系。
(1)含义
指将在空间上连续的图像转换成离散的采样点(即像素)集的操作。
(2)关系
一般来说,采样间隔越大,所得图像像素数越少,空间分辨率低,质量差,严重时出现像素呈块状的国际棋盘效应;采样间隔越小,所得图像像素数越多,空间分辨率高,图像质量好,但数据量大。
2、什么是量化,简述量化等级与图像关系。
(1)含义
是将各个像素所含的明暗信息离散化后,用数字来表示。一般的量化值为整数。
(2)关系
图像的采样点数一定时:量化等级越多,所得图像层次越丰富,灰度分辨率高,图像质量好,但数据量大;量化等级越少,图像层次欠丰富,灰度分辨率低,会出现伪轮廓现象(3bit以下的量化),图像质量变差,但数据量小。
3、简述中值滤波器对不同类型的噪声抑制效果。
(1)对于椒盐噪声,中值滤波的噪声抑制效果比较好
椒盐噪声是幅值近似相等但随机分布在不同位置上,图像中有干净点也有污染点。中值滤波,有较大概率选择到图像中未被噪声污染的点来替代污染点,所以有抑制噪声的作用。
(2)对于高斯噪声,中值滤波的噪声抑制效果不够好
高斯噪声是幅值近似正态分布,但分布在每点像素上。因为图像中的每点都是污染点,所以中值滤波选不到合适的干净点
4、对于一张灰度图像,其梯度是如何定义的?图像梯度的物理意义是什么?
(1)定义
图像 f(x,y) 在其坐标(x,y) 上的梯度是一个二维列向量
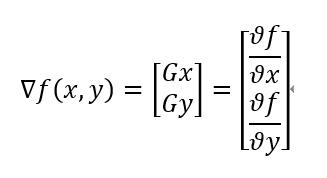
其中 ∇f 的大小为 f(x,y) 的最快变化率,方向为 f(x,y) 的最快变化方向
梯度的模:
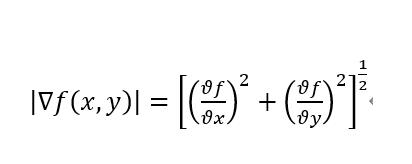
(2)物理意义
任一点(x,y)处一个边缘的方向与该点处的梯度向量的方向正交
在灰度变化平缓的区域其梯度值较小
图像中灰度变化较大的边缘区域梯度值大
在灰度均匀区域其梯度值为零
3.计算(每题15分,共60分)
1、已知灰度图,对该图像进行线性对比度展宽,得到新图像

原图中的重要景物的灰度分布假设在[fa,fb]的范围内,则对比度线性展宽的目的是使处理后图像的重要景物的灰度分布在[ga,gb]的范围内,当
,则可达到
对比度展宽的目的,换句话说,如上图所示的该线性映射关系中的分段直线的斜率有α<1,γ<1表示了非重要景物的抑制,β>1则表示了重要景物的对比度展宽增强。
将对比度线性展宽的计算公式表示如下:

2、直方图均衡化算法的计算
直方图均衡方法的基本原理是:对在图像中像素个数多的灰度值(即对画面其主要作用的灰度值)进行展宽,而对像素个数少的灰度值(即对画面不起主要作用的灰度值)进行归并。从而达到清晰图像的目的。
设f(i,j),g(i,j),(i=1,2,…,M;j=0,1,2,…,N)分别为原图像和处理后的图像,图像的灰度变化范围为[0,255],则直方图均衡化方法的具体步骤如下:
①求原图[f(i,j)]m*n的灰度直方图,设用256维的向量hf表示;
②由hf求原图的灰度分布概率,记作pf,则有

其中,Nf=M xN(M,N分别为图像的长和宽)为图像的总像素个数;
③计算图像各个灰度值的累计分布概率,记作pa,则有
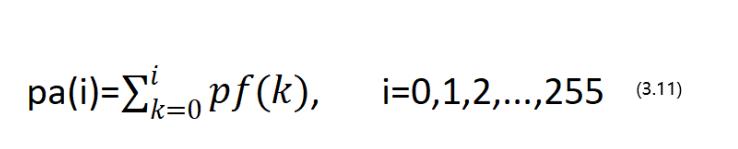
其中,令pa(0)=0。
④进行直方图均衡化计算,得到处理后图像的像素值g(i,j)为:

例:
下面,从一个简单的计算示例来体会直方图均衡化方法

设在这里图像的灰度变化范围**[0,9]**,按照式(3.10),求出
1.原图的灰度直方图为
hf=[3,2,4,4,1,1,4,1,2,3]
(就是把0~9出现的次数统计出来,比如0出现了3次,所以第一个位置为3)
2.图像的总像素数为
Nf=5x5=25
3.原图的灰度分布概率为
pf=[3/25,2/25,4/25,4/25,1/25,1/25,4/25,1/25,2/25,3/25];
4.原图的灰度累计分布概率为
pa=[0,5/25,9/25,13/25,14/25,15/25,19/25,20/25,22/25,25/25]
6.计算原图与新图灰度值的影射关系 (四舍五入)
9*pa=[0, 1.8 ,3.2 ,4.7, 5 ,5.4 ,6.8 ,7.2 ,7.9 ,9 ]
3、基于像素采样的图像缩小方法对图进行缩小

例:
原图

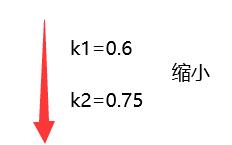

计算方法(四舍五入):
原图x=[1,6], y=[1,6].
新图i=[1,6x0.6]=[1,4],j=[1,6*0.75]=[1,5].确定缩小后的图为4行5列
求原图(1,1),(2,2)(3,3)(4,4)(4,5)缩小后的点
i->x:[1/0.6,2/0.6,3/0.6,4/0.6]=[1.67,3.33, 5,6.67]
=[2,3,5,6],
j->y:[1/0.75,2/0.75 ,3/0.75,4/0.75,5/0.75]=[1.33, 2.67,4, 5.33,6.67]
=[1,3,4,5,6].

4、用3*3的模版对图像进行对称近邻(SNN)均值滤波。
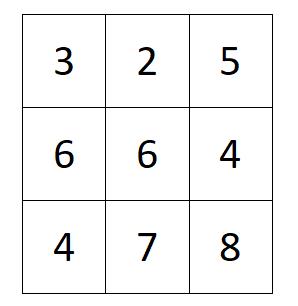
以f(2,2)=6为例,先找到4对对称点
(fm(1,1),fm(3,3))=(3,8),(fm(1,2),fm(3,2))=(2,7)
(fm(1,3),fm(3,1))=(5,4),(fm(2,1),fm(2,3))=(6,4)
在这4对点中,找出与f(2,2)=6灰度值相近的点为
[8,7,5,6]
(就是这点中与6差距小的,比如第一个点(3,8),8差6少些,所以是8)
然后求均值

以上是关于数字图像处理2021期末复习考试重点大纲的主要内容,如果未能解决你的问题,请参考以下文章