机器学习入门系列06，Logistic Regression逻辑回归

Posted 2022-12-05 yofer张耀琦

Gitbook整理地址：https://yoferzhang.gitbooks.io/machinelearningstudy/content/20170409ML06LogisticRegression.html

Step1 逻辑回归的函数集

上一篇讲到分类问题的解决方法，推导出函数集的形式为：

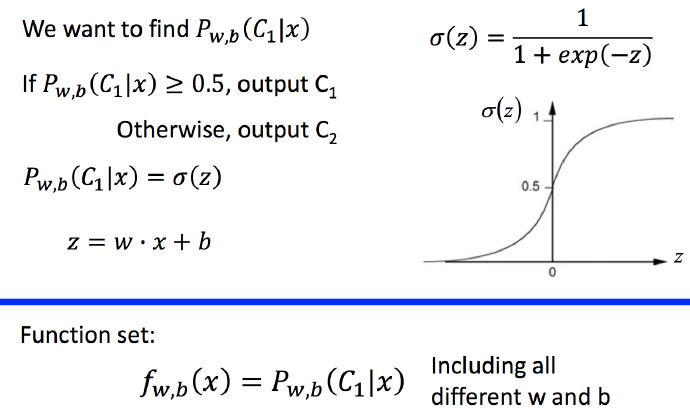
将函数集可视化：

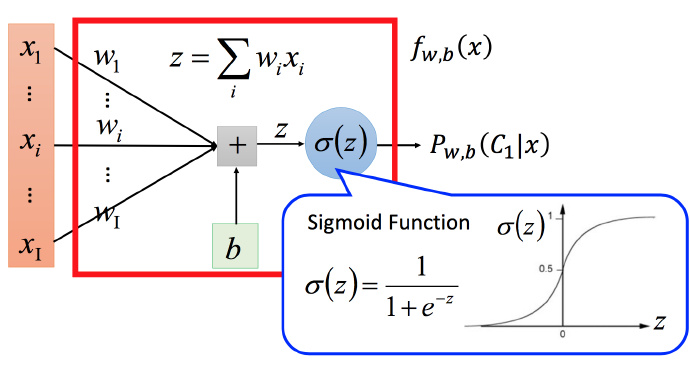
图中z写错了，应该是 $z = \\sum_i w_i x_i + b$。这种函数集的分类问题叫做 Logistic Regression（逻辑回归），将它和第二篇讲到的线性回归简单对比一下函数集：

Step2 定义损失函数

上图有一个训练集，每个对象分别对应属于哪个类型（例如 $x^3$ 属于 $C_2$ ）。假设这些数据都是由后验概率 $f_w,b(x) = P_w, b(C_1 | x)$产生的。

给定一组 w和b，就可以计算这组w，b下产生上图N个训练数据的概率，

$$L(w, b) = f_w,b(x^1)f_w,b(x^2) \\left( 1-f_w,b(x^3) \\right) \\cdots f_w,b(x^N) \\qquad (1-1)$$

对于使得 $L(w, b)$最大的$w$和 $b$，记做$w^*$ 和 $b^*$ ，即：

$$w^*,b^* = \\arg \\max_w,b L(w,b) \\qquad (1-2)$$

将训练集数字化，并且将式1-2中求max通过取负自然对数转化为求min ：

然后将$-\\ln L(w,b)$改写为下图中带蓝色下划线式子的样子：

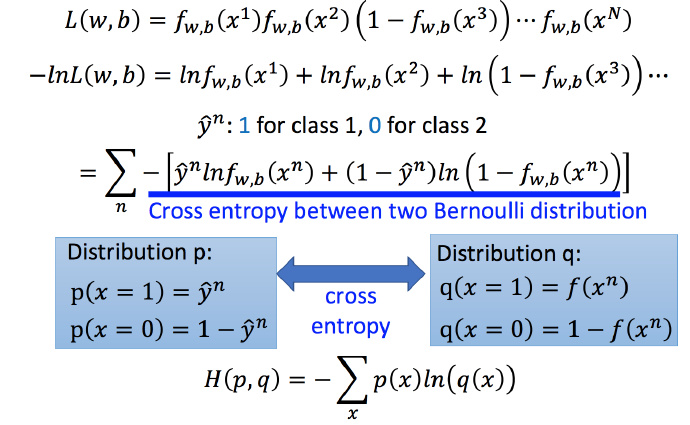
图中蓝色下划线实际上代表的是两个伯努利分布（0-1分布，两点分布）的 cross entropy（交叉熵）

假设有两个分布 p 和 q，如图中蓝色方框所示，这两个分布之间交叉熵的计算方式就是 $H(p,q)$；交叉熵代表的含义是这两个分布有多接近，如果两个分布是一模一样的话，那计算出的交叉熵就是0

交叉熵的详细理论可以参考《Information Theory（信息论）》，具体哪本书我就不推荐了，由于学这门科目的时候用的是我们学校出版的教材。。。没有其他横向对比，不过这里用到的不复杂，一般教材都会讲到。

下面再拿逻辑回归和线性回归作比较，这次比较损失函数：

此时直观上的理解：如果把function的输出和target（真正的function $\\haty^n$）都看作是两个伯努利分布，所做的事情就是希望这两个分布越接近越好。

Step3 寻找最好的function

下面用梯度下降法求：

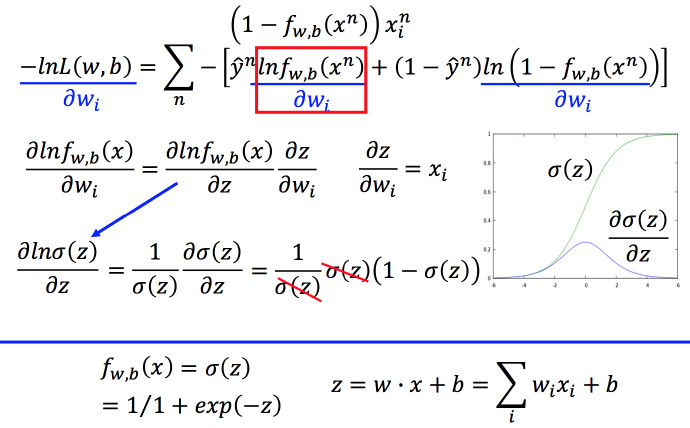
要求$-\\ln L(w,b)$ 对 $w_i$的偏微分，只需要先算出$\\ln f_w,b(x^n)$ 对 $w_i$的偏微分以及 $\\ln \\left( 1- f_w,b(x^n) \\right)$ 对 $w_i$的偏微分。计算$\\ln f_w,b(x^n)$ 对 $w_i$偏微分，$f_w,b(x)$可以用$\\sigma (z)$表示，而$z$可以用以上是关于机器学习入门系列06，Logistic Regression逻辑回归的主要内容，如果未能解决你的问题，请参考以下文章

机器学习 —— 基础整理：线性回归；二项Logistic回归；Softmax回归；广义线性模型

《机器学习实战》Logistic回归算法

MNIST机器学习入门

机器学习实战精读--------logistic回归

PyTorch深度学习-06逻辑斯蒂回归（快速入门）

机器学习笔记—Logistic回归