机器学习-非线性回归( Unlinear Regression) -逻辑回归（Logistic Regression）算法

Posted 2022-12-05 YEN_csdn

学习彭亮《深度学习基础介绍：机器学习》课程

---

概率

定义

概率(Probability): 对一件事情发生的可能性的衡量

范围

0 <= P <= 1

计算方法

• 根据个人置信
• 根据历史数据
• 根据模拟数据

条件概率

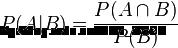
即A在B发生的情况下的概率=AB同时发生的概率/B发生的概率

---

Logistic Regression (逻辑回归)

例子

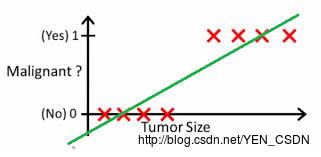
以h(x) > 0.5来区分

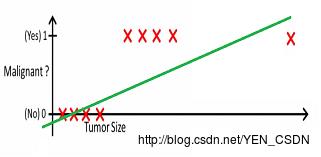
以h(x) > 0.2来区分

---

基本模型

测试数据为X（x0，x1，x2···xn） /* x0...Xn都是自变量 */
要学习的参数为： Θ（θ0，θ1，θ2，···θn）

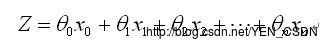
向量表示：
（*）

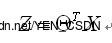处理二值数据，引入Sigmoid函数时曲线平滑化
（**）

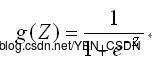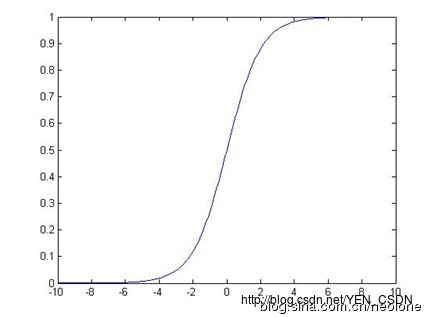用这个函数来模拟0-1之间的变化

由（* * ）（*）=>预测函数为

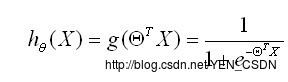
用概率表示
（y==1）
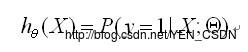(X为自变量，Θ为待求参数，所以此表达式的意思为：给定X，Θ的情况下y=1的概率为多少)
（y==0）
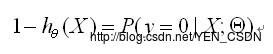（所以此表达式的意思为：给定X，Θ的情况下y=1的概率为多少）

---

Cost函数

线性回归：

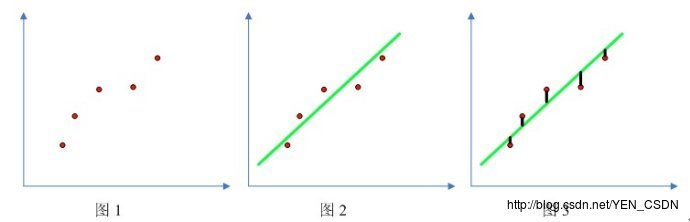
直线的标准为：预测点和真实点距离的平方最小，即

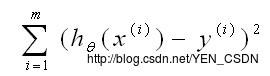
• m:m个实例
• y(i):第i个实例的真实值为多少
• x(i):每个实例自变量是多少
• h(x(i)):每个实例自变量套用h(z)这个方程的函数值，即预测值（y_hat）

---

在线性方程中Cost函数：

此线性方程的目标就是要找到合适的 θ0，θ1使上式最小（即最小的Cost）

在回归方程中Cost函数：

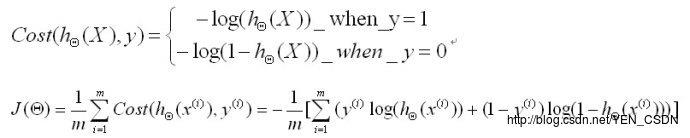
（要找最小，所以加了-号；取对数方便加减、求导；把y=1时和y=0时的方程合并为J(Θ) ）

所以现在的目标就是通过训练集训练并学习出一组Θ的值，使目标函数J(Θ)最小化

---

解法：梯度下降（Gradient Decent）

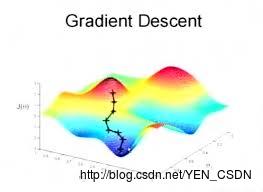
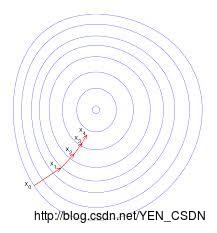
对于多元非线性函数的高维平面，从平面上的一个点出发，目标是找到一组Θ的值，使目标函数J(Θ)最小化，也就是找到上图中的最低点。所以就是梯度下降法：从某个点出发，求偏导，走下降的最快的，求导后找到斜率最大的方向，再走一步，重复…直到找到最低点

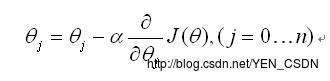
J(Θ)对Θj求偏导
alpha：学习率，就是每一步的步长
即每一步传进来后通过Θj-alpha*（J(Θ)对Θj求偏导）得到下一步的Θj

更新法则

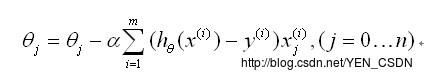
• alpha:学习率
• i：不同的实例
• 同时对所有Θ进行更新，重复更新直至收敛（小于设定的阈值）

---

#coding=utf-8

# @Author: yangenneng
# @Time: 2018-01-18 15:30
# @Abstract：非线性回归-逻辑回归算法

import numpy as np
import random

'''
# function:产生一些数据，用来做拟合
# numPoints：实例个数
# bias：随机生成y时的偏好
# variance：一组数据的方差
'''
def genData(numPoints,bias,variance):
    # 生成numPoints行2列的零矩阵  shape形状
    x = np.zeros(shape=(numPoints, 2))
    y = np.zeros(shape=(numPoints))
    # 循环numPoints次，及i=0 到 numPoints-1
    for i in range(0,numPoints):
        x[i][0] = 1
        x[i][1] = i
        # random.uniform(0,1)  从0-1之间随机产生一些数
        y[i] = (i+bias)+random.uniform(0, 1) * variance
    return x, y


'''
# 梯度下降算法
# x：自变量矩阵，每行表示一个实例
# y：实例的真实值
# theta：待求的参数
# alpha：学习率
# m：总共m个实例
# numIterations：重复更新的次数（重复更新直至收敛（小于设定的阈值））
'''
def gradientDescent(x,y,theta,alpha,m,numIterations):
    # 矩阵转置
    xTran = np.transpose(x)
    # 循环次数
    for i in range(0,numIterations):
        # 公式中的Z
        hypothesis = np.dot(x,theta)
        # loss:预测值-实际值
        loss = hypothesis-y
        # cost就是公式中J(Θ)，这里定义的是一个简单的函数
        cost = np.sum(loss ** 2) / (2 * m)
        # 每次更新的更新量，即更新法则
        gradient=np.dot(xTran,loss)/m
        # Θ
        theta = theta-alpha * gradient
        print ("Iteration %d | cost :%f" % (i, cost))
    return theta

# 参数数据
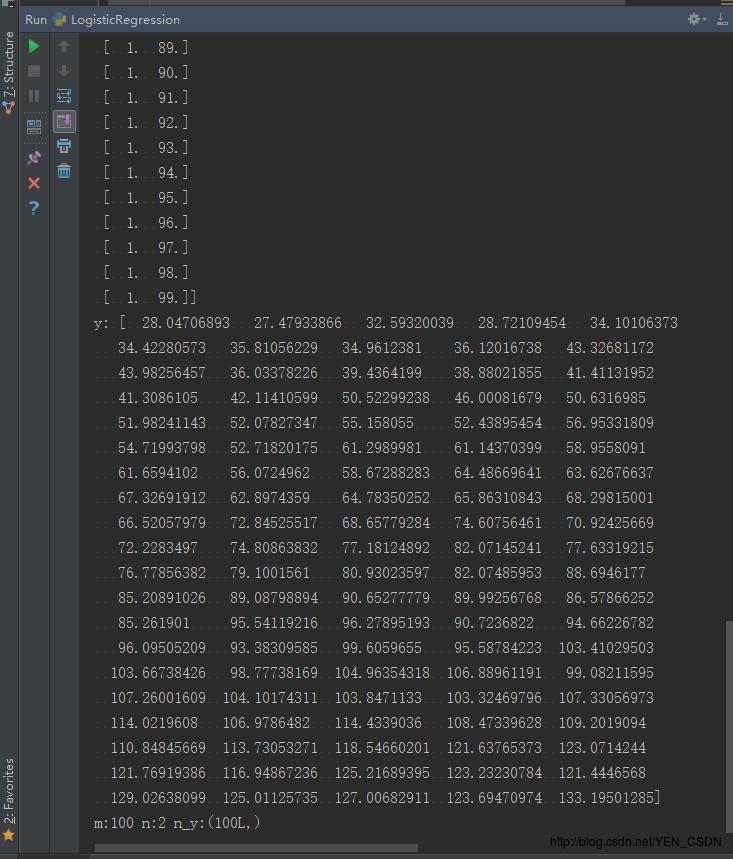
x,y = genData(100, 25, 10)
print "x:", x
print "y:", y

# 查看产生数据的行列
m,n = np.shape(x)
n_y = np.shape(y)
print("m:"+str(m)+" n:"+str(n)+" n_y:"+str(n_y))

# 求Θ
numIterations = 100000
alpha = 0.0005
theta = np.ones(n)
theta= gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)

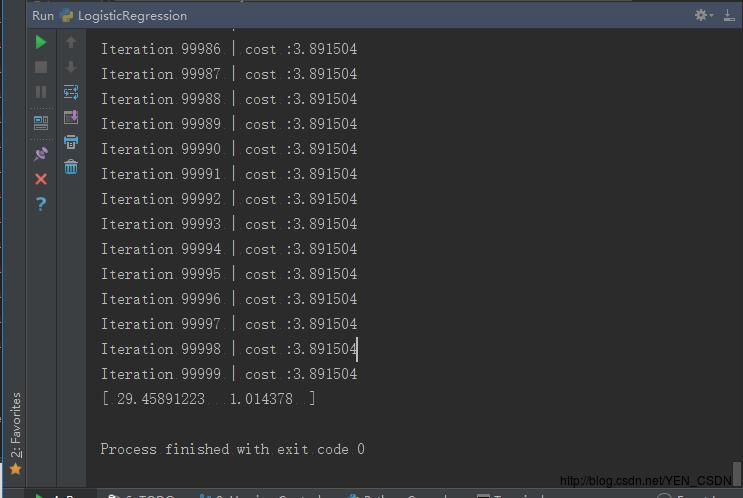
[ 29.45891223 1.014378 ]表示Θ1、Θ2（因为X是二维的）