matlab改进大规模邻域搜索算法求解路径优化

Posted 2022-12-05 张叔zhangshu

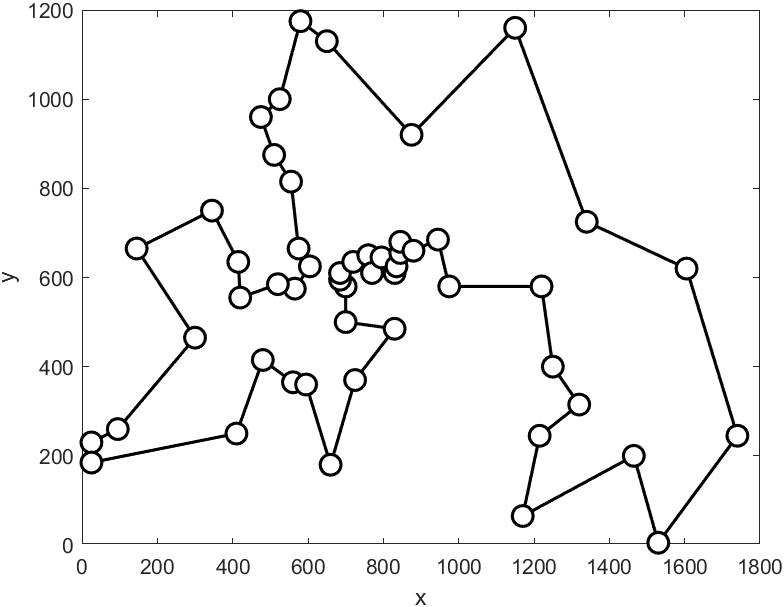
近年来，随着环境问题的日益突出，越来越多物流配送企业开始使用节能环保的电动物流车。 但是由于续航里程有限及充电设施布局不完善等问题，电动车并不能完全代替燃油车，所以大多物流企业目前主要采用电动车与燃油车混合配送的过渡模式。 与燃油车配送不同，由于电动车需途中进行充电，改变了原有配送系统的配置参数，并对配送时间窗产生影响；此外，实际配送过程中配送中心会在车辆离开后继续接收新的需求，导致配送系统的状态不断发生变化，需要对已有配送方案重新进行调整。 如果不能合理快速地规划与调整配送路线，不仅会大幅增加企业的运营成本，还会降低顾客服务水平。 因此，研究电动车与燃油车混合配送模式下的动态需求车辆路径问题具有重要的现实意义。车辆路径优化（ｖｅｈｉｃｌｅ ｒｏｕｔｉｎｇ ｐｒｏｂｌｅｍ，ＶＲＰ） 一直都是物流配送领域中的热点问题，从 １９５９ 年 ＶＲＰ 被 Ｄａｎｔｚｉｇ 和 Ｒａｍｓｅｒ提出后就受到了国内外学者的广泛关注，目前已有非常丰硕的研究成果。 结合各种现实场景，研究人员开始对基础的ＶＲＰ 进行扩展研究，如有载重约束的 ＶＲＰ（ＣＶＲＰ）［２］、带时间窗约束的 ＶＲＰ（ＶＲＰＴＷ）［３］、多车型 ＶＲＰ（ＨＶＲＰ）［４］等。 使用电动物流车的 ＶＲＰ 称为电动车车辆路径问题（ＥＶＲＰ），Ｃｏｎｒａｄ等人［５］首次对 ＥＶＲＰ 进行研究，在允许车辆途中充电的条件下，建立使用车辆数目最少以及行驶成本、服务时间成本和充电成本最小的多目标模型；Ｓｃｈｎｅｉｄｅｒ 等人［６］进一步提出了带时间窗的 ＥＶＲＰ，建立使用车辆数最小和总行驶成本最小的优化模型，并设计了基于变邻域搜索和禁忌搜索的混合算法；葛显龙等人［７］考虑到充电时间对时间窗的违反会存在影响，提出带软时间窗的 ＥＶＲＰ，建立了行驶成本、路径成本以及车辆使用成本为目标函数的数学模型，并设计了节约里程算法加改进的禁忌搜索算法进行求解；Ｋｅｓｋｉｎ 等人［８］针对带时间窗的电动车车辆路径问题，考虑电动车在充电站采取部分充电的情况，设计了自适应大规模邻域搜索算法进行求解；Ｐｅｌｌｅｔｉｅｒ 等人［９］考虑电动车耗电为非线性的情况，研究天气、道路情况以及司机行为等不确定因素背景下的电动车车辆路径问题，通过将问题定义为鲁棒混合整数线性规划模型，并设计一种基于大规模邻域搜索的两阶段启发式算法进行求解；Ａｌｅｓｉａｎ 等人［１０］提出了可以多次访问充电站的电动车车辆路径问题，并采用一种带有学习策略的进化遗传算法找到最小化成本（与行驶时间、充电时间、能源消耗相关） 的车辆配送路线；Ｙａｎｇ 等人［１１］考虑了分时电价的情况，采用可学习的遗传算法实现对车辆路径以及充电时间的同时优化。 如果在同一配送系统中同时使用不同类型的车辆进行配送，考虑因素更多，问题更加复杂。Ｇｏｅｋｅ 等人［１２］首次对带时间窗的电动车与燃油车的混合配送问题（ＥＶＲＰＴＷＭＦ）进行研究，并设计了自适应大规模邻域搜索算法进行求解；Ｈｉｅｒｍａｎｎ 等人［１３］考虑带时间窗的同时使用传统燃油车、插电式混合动力车以及电动车三种车型的车辆路径问题，并设计基于遗传算法以及局部和大规模邻域搜索算法的混合启发式算法进行求解。以上研究均属于静态 ＶＲＰ，即所有客户需求可以事先确定。 但在实际配送过程中，配送中心会在车辆运行途中继续接收新客户的配送需求，并对已有车辆路线重新进行规划，此类问题即动态需求的 ＶＲＰ（ＤＤＶＲＰ）。 Ｈｏｎｇ［１４］研究带硬时间窗的 ＤＤＶＲＰ，并将动态问题分为一系列的静态问题，设计了改进的大规模邻域搜索算法对该问题进行求解；Ｄｅ Ａｒｍａｓ 等人［１５］将车辆工作时间不同、顾客有多个时间窗、顾客之间存在优先级等现实因素考虑到动态车辆路径问题中，并用变邻域搜索算法求解；Ｃｈｅｎ 等人［１６］进一步采用自适应大规模邻域搜索算法进行 ＤＤＶＲＰ 的求解；张文博等人［１７］针对带时间窗的 ＤＤＶＲＰ 设计了遗传算法以及模拟退火结合的两阶段算法；李阳等人［１８］针对带载重约束的动态需求车辆路径问题，提出了一种延迟服务机制，且采用混合变邻域人工蜂群算法进行多阶段求解。综上所述，目前 ＤＤＶＲＰ 已有一定的研究成果，但是这些研究都是基于传统燃油车。 邵赛等人［１９］首次将电动车引入动态需求车辆路径问题中，研究了不考虑客户时间窗的电动车配送的 ＤＤＶＲＰ。 通过国内外的文献检索，目前还没有发现其他针对电动车的 ＤＤＶＲＰ 的研究，此外也未有针对电动车与燃油车混合配送模式下的 ＤＤＶＲＰ 的研究。 不同于单一燃油车或电动车 ＤＤＶＲＰ，混合配送模式将电动车与燃油车这两种具有不同配送特点的车辆纳入同一配送系统同步考虑，限制因素更多，尤其需同时考虑动态需求和客户时间窗，模型构建与求解将更为复杂。 考虑到该类问题在企业日常运营中会越来越普遍，本文研究了电动车与燃油车混合配送模式下带时间窗的动态需求车辆路径问题（ｅｌｅｃｔｒｉｃ ｖｅｈｉｃｌｅ ｒｏｕｔｉｎｇ ｐｒｏｂｌｅｍ ｗｉｔｈ ｔｉｍｅｗｉｎｄｏｗｓ ａｎｄ ｍｉｘｅｄ ｆｌｅｅｔ ｃｏｎｓｉｄｅｒｉｎｇ ｄｙｎａｍｉｃ ｄｅｍａｎｄｓ，ＥＶＲＰＴＷＭＦ⁃ＤＤ）。 此外，考虑到动态需求对实时性要求较高，而本文研究的 ＥＶＲＰＴＷＭＦ⁃ＤＤ 又属于 ＮＰ⁃ｈａｒｄ 问题，用精确算法求解较为困难且时间成本高。 因此，本文根据所建模型的特点设计了改进的自适应大规模邻域搜索算法，以期在较短的时间内获得较优的配送方案。１　 问题描述ＥＶＲＰＴＷＭＦ⁃ＤＤ 可描述为某物流企业使用电动车和燃油车为 Ｎ 个有时间窗要求的顾客提供配送服务。 首先，对上一工作日的预约静态客户制定配送路线并进行送货，在配送过程中，若出现新的客户需求，需要对正在配送的车辆路径进行重新规划或派出新车进行服务。 此外，电动车由于续航里程有限，在配送过程中需要到公共充电站充电才能继续进行配送任务。 该问题的求解目标是寻找车辆行驶总成本最小化的最优路径。 模型的假设条件如下：ａ） 每个客户点只能被一辆车服务，每辆车可以服务多个客户点，车辆在完成配送服务后要驶回配送中心；ｂ）电动车从配送中心出发时电池为满电，并且允许在行驶过程中采用满充的方式进行多次充电，充电站可以被多次访问。 为了更好地描述问题，给出如图 １ 所示的简单示例。 本文建立了 ＥＶＲＰＴＷＭＦ⁃ＤＤ 的两阶段 ０⁃ １ 整数规划模型，包括初始阶段优化模型和动态阶段优化模型。２　 模型构建２􀆰 １　 初始阶段优化模型初始阶段主要对已经预约的静态客户点进行路线设计，得到初始的配送路径优化方案。 模型所用参数与变量如表 １ 所示。 初始阶段优化模型构建如下：

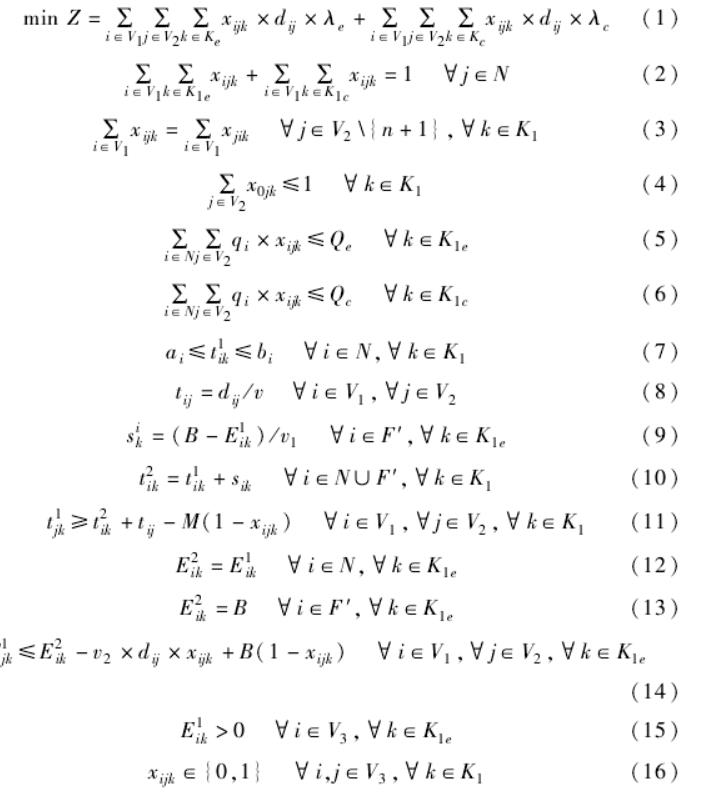
　 　本；式（２）表示每个客户只能被访问一次；式（３） 为流守恒约束；式（４）表示每辆车最多服务一条路径且从配送中心出发；式（５）表示电动车配送的任务总量不能超过其最大载重；式（６）表示燃油车的配送任务总量不能超过其最大载重量；式（７）表示要满足客户点ｉ 的服务时间窗要求；式（８）表示从点ｉ到 ｊ 的行驶时间为两点之间距离与速度的比值；式（９）表示电动车在充电站充电时间的计算；式（１０）表示车辆在到达和离开点 ｉ 的时间关系；式（１１）表示车辆到达点ｊ 的时间为前边行驶时间的累计；式（１２）表示电动车到达和离开客户点的电量不发生改变；式（１３）表示电动车在充电站满充；式（１４）表示电动车从点 ｉ 行驶到点 ｊ 的电量消耗关系；式（１５）表示电动车到达每一个点的电量都要大于 ０；式（１６）为 ０⁃１ 变量约束条件式（１）为目标函数，最小化包含电动车与燃油车的运输成

（１）为目标函数，最小化包含电动车与燃油车的运输成

主程序

tic
clear
clc
%% 输入数据
dataset=importdata('input.txt');                %数据中，每一列的含义分别为[序号，x坐标，y坐标]
x=dataset(:,2);                                 %x坐标
y=dataset(:,3);                                 %y坐标
vertexes=dataset(:,2:3);                        %提取各个城市的xy坐标
h=pdist(vertexes);
dist=squareform(h);                             %距离矩阵
%% 参数初始化
MAXGEN=300;                                     %最大迭代次数
%% 构造初始解
[Sinit,init_len]=construct_route(dist);         %贪婪构造初始解
init_length=route_length(Sinit,dist);
str1=['初始总路线长度 =  ' num2str(init_length)];
disp(str1)
%% 初始化当前解和全局最优解
Scurr=Sinit;
curr_length=init_length;
Sbest=Sinit;
best_length=init_length;
%% 主循环
gen=1;
BestL=zeros(MAXGEN,1);                          %记录每次迭代过程中全局最优个体的总距离
while gen<=MAXGEN
    %% “破坏”解
    [Sdestroy,removed]=destroy(Scurr);
    %% “修复”解
    [Srepair,repair_length]=repair(removed,Sdestroy,dist);
    if repair_length<curr_length
        Scurr=Srepair;
        curr_length=repair_length;
    end
    if curr_length<best_length
        Sbest=Scurr;
        best_length=curr_length;  
    end
    %% 打印当前代全局最优解
    disp(['第',num2str(gen),'代最优路线总长度 =  ' num2str(best_length)])
    BestL(gen,1)=best_length;
    %% 计数器加1
    gen=gen+1;
end
str2=['搜索完成！ 最优路线总长度 =  ' num2str(best_length)];
disp(str2)
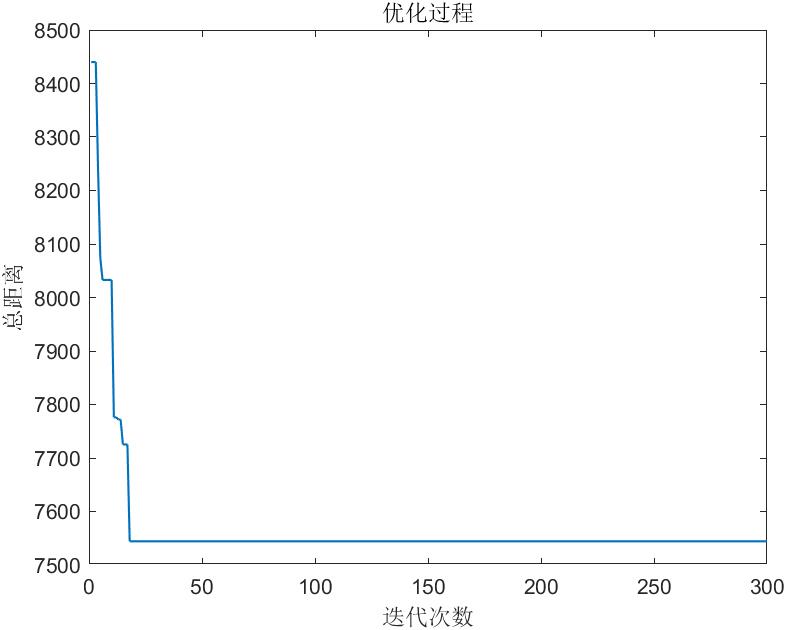
%% 画出优化过程图
figure;
plot(BestL,'LineWidth',1);
title('优化过程')
xlabel('迭代次数');
ylabel('总距离');
%% 画出全局最优路线图
plot_route(Sbest,x,y);
toc

改进算法构造初始解

%% 贪婪算法构造TSP的初始解
%输入dist：             距离矩阵   
%输出init_route：      贪婪算法构造的初始路线
%输出init_len：        init_route的总距离  
function [init_route,init_len]=construct_route(dist)
N=size(dist,1);                     %城市数目
%先将距离矩阵主对角线上的0赋值为无穷大
for i=1:N
    for j=1:N
        if i==j
            dist(i,j)=inf;
        end
    end
end

unvisited=1:N;                      %初始未被安排的城市集合
visited=[];                         %初始已被安排的城市集合

min_dist=min(min(dist));            %找出距离矩阵中的最小值
[row,col]=find(dist==min_dist);     %在dist中找出min_dist所对应的行和列
first=row(1);                       %将min_dist在dist中所对应行序号作为起点

unvisited(unvisited==first)=[];     %将first从unvisit中删除
visited=[visited,first];            %把first添加到visit中
pre_point=first;                    %将fisrt赋值给pre_point
while ~isempty(unvisited)
    pre_dist=dist(pre_point,:);     %pre_point与其它城市的距离
    pre_dist(visited)=inf;          %将pre_point与已经添加进来的城市之间的距离设位无穷大
    [~,pre_point]=min(pre_dist);    %找出pre_dist中的最小值
    unvisited(unvisited==pre_point)=[]; %将pre_point从unvisit中删除
    visited=[visited,pre_point];        %把pre_point添加到visit中
end
init_route=visited;
init_len=route_length(init_route,dist); %计算init_route的总距离
end

代码下载连接