认识二分法

Posted 2022-12-05 dxj1016

5、二分法

时间复杂度：O(logn)

5.1、有序数组找某数是否存在

题目：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

class Solution 
    public int search(int[] nums, int target) 
        int left = 0, right = nums.length;
        while (left < right) 
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid;
        
        return -1;
    

5.2、有序数组中找大于等于某个数的最左位置

package 左神算法.二分查找;

public class FindSort
    public static void main(String[] args) 
        int[] arr = 1,2,3,4,5,6;
        int target = 3;
        System.out.println(searchTarget(arr, target));
        System.out.println(nearLeftIndex(arr, target));
    
//找某个数的位置
    public static int searchTarget(int[] arr, int target) 
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) 
            int mid = left + ((right - left) >> 1);
            if (arr[mid] == target) 
                return mid;
             else if (arr[mid] < target) 
                left = mid + 1;
             else if (arr[mid] > target) 
                right = mid;
            
        
        return -1;
    
//找大于等于某个数的最左位置
    public static int nearLeftIndex(int[] arr, int target) 
//        判断极端情况
        if (arr == null || arr.length == 0) 
            return -1;
        
        int left = 0;
        int right = arr.length - 1;
//        记录最左的值的位置
        int index = -1;
        while (left <= right) 
            int mid = left + ((right - left) >> 1);
            if (arr[mid] >= target) 
                index = mid;
                right=mid-1;
             else 
                left = mid + 1;
            
        
        return index;
    

5.3、局部最小值问题

在一个数组中，元素是无序的，而且知道相邻的两个数一定不相等。使用局部最小找到时间复杂度比O(n)好的方法。

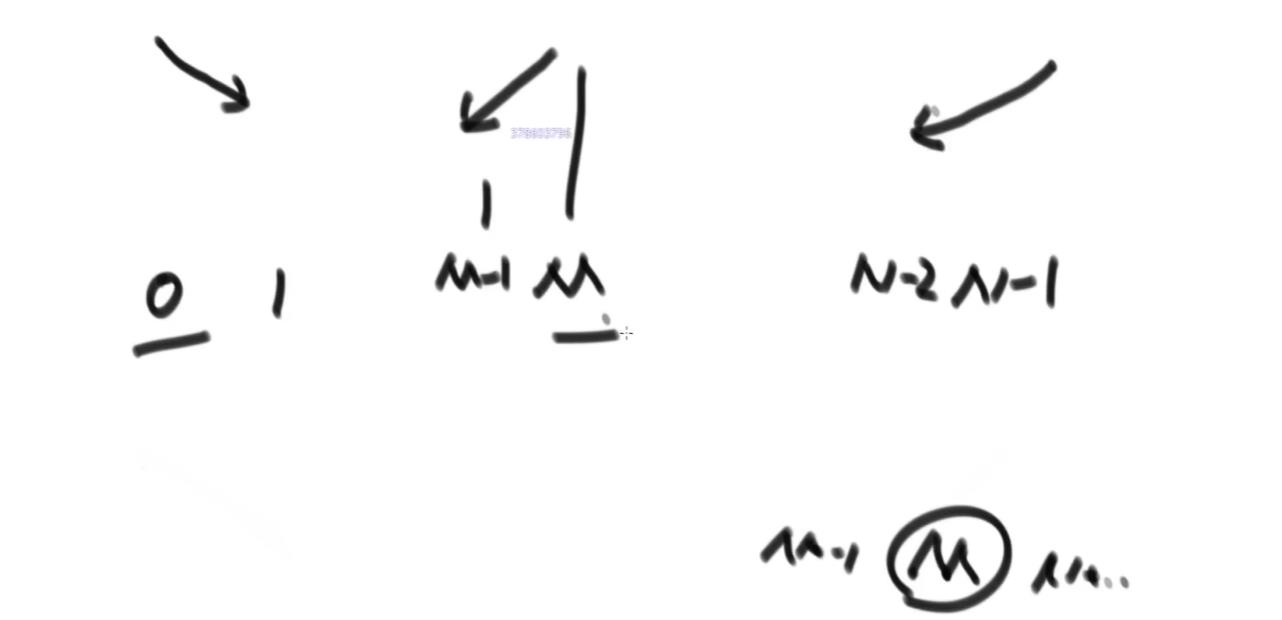
相邻两个数不相等， 那么两个数之间必定有一个小一个大，这时候找局部最小的，比如0-1中的1是最小的；n–2到n-1中n-2是最小的的，那么趋势就是两边都向下，这样的话在0-n-1之间肯定存在一个最小值；所以可以采用二分法计算；选择二分的位置；比较二分的前一个和后一个，看那个是比m是小的，小的话那么从0-m-1之间又存在最小值，所以又把问题分解成一半了，继续取二分位置。