基于FPGA的数据采集系统
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于FPGA的数据采集系统相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
数据采集是指将模拟量采集转换成数字量后,再由计算机进行存储、处理、显示或打印的过程,相应的系统称为数据采集系统。随着科技进步,人们对数据采集的要求也越来越高,比如采样频率,分辨率等等。基于单片机的数据采集系统数据处理能力比较低,已经无法达到某些要求。科技的不断创新及半导体工业的发展使得我们将可编程逻辑器件的技术应用到数据采集系统的研究上。同时利用CPLD 强大的数字处理功能和高密集成的特点,降低了硬件的成本,简化了电路设计,具有很好的经济效益和社会效益。有此看出,数据采集系统日趋成熟,应用越来越广泛,发展前景是相当广阔的。
在计算机广泛应用的今天,数据采集的重要性是十分显著的。它是计算机与外部物理世界连接的桥梁。在工业,工程,生产车间等部门,尤其是在对信息实时性能要求较高或者恶劣的数据采集环境中更突出其应用的必要性。这就要求数据采集系统必须具备更高的采样频率,更高的分辨率,来提供更多的原始数据。以前的数据采集系统一般都是以单片机为核心的,随着数据采集要求的不断提高,单片机为核心的数据采集系统已经不能满足要求了。科技进一步发展,就出现了现在的高速数据采集系统,本课题我们将设计基于CPLD的数据采集系统。
设计一个基于FPGA的数据采集系统,以上述信号为主,其中上路信号的周期为117.6ms。采集计算出t1 t2 t3 t4后,然后计算:
m1=-0.5*(cos((6.2831*t1)/117.6)- cos((6.2831*(t1+t2)/117.6)+ cos((6.2831*(t1+t2+t3)/117.6)- cos((6.2831*(t1+t2+t3+t4)/117.6))
m2=-0.5*(sin((6.2831*t1)/117.6)- sin((6.2831*(t1+t2)/117.6)+ sin((6.2831*(t1+t2+t3)/117.6)- sin((6.2831*(t1+t2+t3+t4)/117.6))时间单位是ms,并记录m1m2的值,得到一系列数据。
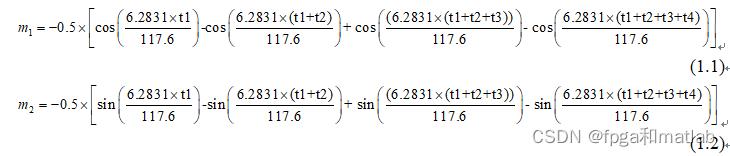
时间单位是ms,并记录m1,m2的值,得到一系列数据,这个信号很短,最多30s就停止了。仿真时我认为可以给系统指定信号,用来验证系统是否准确。
数据采集是指将模拟量采集转换成数字量后,再由计算机进行存储、处理、显示或打印的过程,相应的系统称为数据采集系统。随着科技进步,人们对数据采集的要求也越来越高,比如采样频率,分辨率等等。基于单片机的数据采集系统数据处理能力比较低,已经无法达到某些要求。科技的不断创新及半导体工业的发展使得我们将可编程逻辑器件的技术应用到数据采集系统的研究上。同时利用FPGA 强大的数字处理功能和高密集成的特点,降低了硬件的成本,简化了电路设计,具有很好的经济效益和社会效益。有此看出,数据采集系统日趋成熟,应用越来越广泛,发展前景是相当广阔的。
在计算机广泛应用的今天,数据采集的重要性是十分显著的。它是计算机与外部物理世界连接的桥梁。在工业,工程,生产车间等部门,尤其是在对信息实时性能要求较高或者恶劣的数据采集环境中更突出其应用的必要性。这就要求数据采集系统必须具备更高的采样频率,更高的分辨率,来提供更多的原始数据。以前的数据采集系统一般都是以单片机为核心的,随着数据采集要求的不断提高,单片机为核心的数据采集系统已经不能满足要求了。科技进一步发展,就出现了现在的高速数据采集系统,本课题我们将设计基于FPGA的数据采集系统。
由于数字信号的抗干扰性和精度等方面都比模拟信号信号优越,所以在现代信号处理中,一般都是将模拟信号采样、量化、编码成为数字信号之后再处理。奈奎斯特(Nyquist)采样定理告诉我们:对于一个频带有限信号x(t),其频带限制在内,如果以不小于的采样率对x(t)进行等间隔采样,得到时间离散的采样信号x(n),原信号x(t)就能被采样信号x(n)完全恢复。
从数学上可以进一步证明Nyquist采样定理,也就是推导用离散采样值x(n)表示带限信号x(t)的数学表达式,多种文献对此有详细推导,故这里不再赘述,只给出结果。

AD芯片型号比较多,但是工作原理基本一致,本章节,我们以最常见的AD0809为例子来介绍AD芯片的工作原理。
ADC0809 是8位逐次逼近型A/D转换器。它由一个8路模拟开关、一个地址锁存译码器、一个A/D 转换器和一个三态输出锁存器组成。多路开关可选通8个模拟通道,允许8 路模拟量分时输入,共用A/D 转换器进行转换。三态输出锁器用于锁存A/D 转换完的数字量,当OE 端为高电平时,才可以从三态输出锁存器取走转换完的数据。
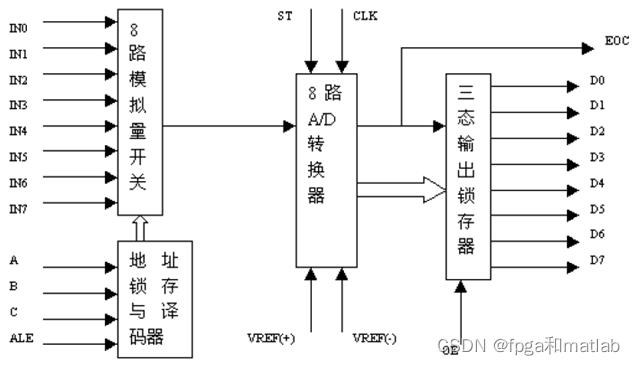
其中,IN0-IN7为8 条模拟量输入通道;电压范围是0-5V;地址输入和控制线:4条。当ALE线为高电平时,地址锁存与译码器将A,B,C三条地址线的地址信号进行锁存,经译码后被选中的通道的模拟量进转换器进行转换。A,B和C为地址输入线,用于选通IN0-IN7上的一路模拟量输。
数字量输出及控制线:11条,ST为转换启动信号。当ST上跳沿时,所有内部寄存器清零;下跳沿时,开始进行A/D转换;在转换期间,ST应保持低电平。EOC为转换结束信号。当EOC为高电平时,表明转换结束;否则,表明正在进行A/D转换。OE为输出允许信号,用于控制三条输出锁存器向单片机输出转换得到的数据。OE=1,输出转换得到的数据;OE=0,输出数据线呈高阻状态。D7-D0为数字量输出线。CLK为时钟输入信号线。因ADC0809的内部没有时钟电路,所需时钟信号必须由外界提供,通常使用频率为500KHZ。
算法的具体步骤如下所示:
步骤一:边沿检测

步骤二:计数器计数
当系统接收到质量信号的时候,则计数器开始技术,当系统检测到F的第一个高电平的时候,则检测时间t1的计算公式如下所示:

将N1的值通过上述的公式进行计算,得到t1,然后计数器同时清零,然后计数器重新开始计数,当检测第二个F的高电平的时候,依次类推,计算对应的时间t2,t3,t4。
根据上述的原理,可以得到四个时间如下所示:

步骤三:计算值得量化处理
由于数字信号处理过程中,其对应的值都是二进制整数数值,而公式3.8的计算结果往往是带小数的。这里以一个实际例子来分析在CPLD中的处理过程。
二、核心程序
always @(posedge i_clk or posedge i_rst)
begin
if(i_rst)
begin
cnt1 <= 16'd0;
cnt2 <= 4'd0;
o_t1s<= 16'd0;
o_t2s<= 16'd0;
o_t3s<= 16'd0;
o_t4s<= 16'd0;
end
else begin
if(i_command==1'b1 | o_edge==1'b1)
cnt1 <= 16'd0;
if(i_command==1'b0 & o_edge==1'b0)
cnt1 <= cnt1+16'd1;
if(i_command==1'b0 & o_edge==1'b1)
cnt2 <= cnt2 + 4'd1;
if(i_command==1'b1 & o_edge==1'b0)
cnt2 <= 4'd0;
if(cnt2 == 0 & o_edge==1'b1)
o_t1s <= cnt1;
if(cnt2 == 1 & o_edge==1'b1)
o_t2s <= cnt1;
if(cnt2 == 2 & o_edge==1'b1)
o_t3s <= cnt1;
if(cnt2 == 3 & o_edge==1'b1)
o_t4s <= cnt1;
end
end
assign o_t1_cur = i_t0 +o_t1s+1;
assign o_t2_cur = o_t1_cur+o_t2s+1;
assign o_t3_cur = o_t2_cur+o_t3s+1;
assign o_t4_cur = o_t3_cur+o_t4s+1;
always @(posedge i_clk or posedge i_rst)
begin
if(i_rst)
begin
o_t1 <= 16'd0;
o_t2 <= 16'd0;
o_t3 <= 16'd0;
o_t4 <= 16'd0;
end
else begin
if(cnts == i_T)
begin
o_t1 <= 16'd0;
o_t2 <= 16'd0;
o_t3 <= 16'd0;
o_t4 <= 16'd0;
end
if(cnts < i_T & cnt2 == 3 & o_edge==1'b1)
begin
o_t1 <= o_t1_cur+i_cycle*cnt0;
o_t2 <= o_t2_cur+i_cycle*cnt0;
o_t3 <= o_t3_cur+i_cycle*cnt0;
o_t4 <= o_t4_cur+i_cycle*cnt0;
end
三、测试结果
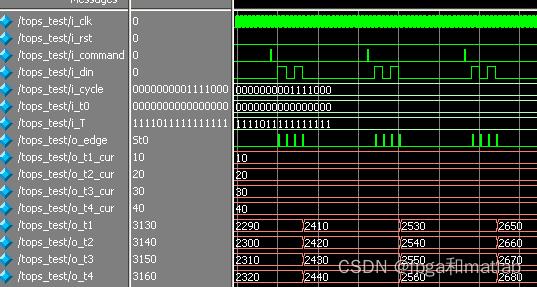
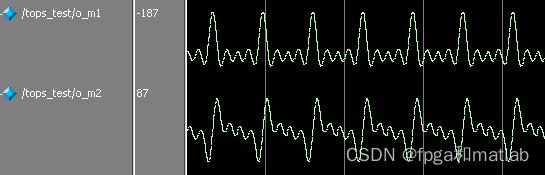
A28-10
以上是关于基于FPGA的数据采集系统的主要内容,如果未能解决你的问题,请参考以下文章