LQ0159 无穷分数计算精度

Posted 2022-12-04 海岛Blog

题目来源：蓝桥杯2015初赛 Java C组C题

题目描述
本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

无穷的分数，有时会趋向于固定的数字。

请计算下图所示的无穷分数，要求四舍五入，精确到小数点后 5 位，小数位不足的补 0。

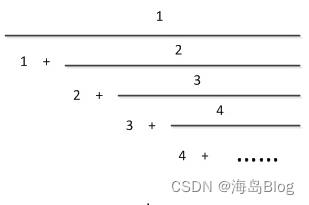
问题分析
这是一个精度有关的问题。
这个题需要找到n与f(n)的关系：
f(1) = 1 / (1 + 1)
f(2) = 1 / (1 + 2 / (2 + 1))
…
其实，这个关系是不那么明确的。
那么可以得到递推关系
f(n) = n / (n + 1)
f(n - 1) = (n - 1) / ((n - 1) + f(n))
…
f(1) = 1 / (1 + f(2))
这个递推关系是从到到小的，最终的f(1)为原公式的值。
解题程序中，实现了一个迭代计算的C语言函数f()用来计算f(n)，再给出若干项的值，用肉眼看算到哪里就满足精度要求。好在看几项就知道了。
更为精确的做法是编程判定。

AC的C语言程序如下：

/* LQ0159 无穷分数 */

#include <stdio.h>

double f(int n)

    double a = 1.0;
    for(int b = n; b >= 1; b--)
      a = b / (b + a);
    return a;


int main()

//    for (int i = 1; i <= 10; i++)
//        printf("%d %.5f\\n", i, f(i));

    printf("%.5f\\n", f(6));

    return 0;