小球称重的解法整合 N个小球有一个坏球，最少几次能找出坏球

Posted 2022-12-03 Lejeune

小球称重的解法整合 N个小球有一个坏球，最少几次能找出坏球
    最近在看小球称重的问题，之前只记住了公式，最近回过来看，发现知乎上多了一些优质答案，遂记录一下。

    现附上学习地址

    先说结论，
N 个乒乓球中有一个和其他的质量不同，用天平最少几次一定能称出来？（并知道是轻了还是重了）
n次操作最多能解决以下个数的问题
$$\frac{3^n-3}{2}$$
本文主要也阐述解决这个问题的方法。

N 个乒乓球中有一个和其他的质量不同，用天平最少几次一定能称出来？（不必知道轻了还是重了）
n次操作最多能解决以下个数的问题
$$\frac{3^n-1}{2}$$

主要方法有如下几种

文章目录

• • • • • 信息论
        • 三进制正逆序
        • 快速排序
        • 决策树
        • 矩阵
        • 递归

信息论

特点

1. 简单暴力
2. 容易理解
3. 只能用于估计，答案在有些情况下是不对的
4. 无法知道其具体操作过程，但是可以理论上估计操作次数

    依托于香农的信息论，可以知道N个球的信息熵，以999个球的称重为例（不加以说明，下面都以999为例），每一个球都有可能成为异常球，如果是异常球，又有可能是轻或者重两种可能，所以一共有999*2的可能性，他的信息熵为 $$\frac{\log (999\ast 2)}{\log 2}=10.97$$
而每次称重最多有三个状态，每次可获得的最大信息熵为（注意此处）
$$\frac{\log 3}{\log 2}=1.58$$
所以应当有10.97/1.58次操作，计算后向上取整为7次。

值得注意的是，此处可获得的最大信息熵，我的理解是，每一次都做到可能性变为原来的1/3时才可行，考虑正好是3的指数个数时，每次都3等分称重，不论是相等还是有轻有重，都可以将可能性降为原来的1/3，这样这个公式才成立。但是实际上小球也存在不被等分的情况，这里默认可以被分为小数，但显然是不合规矩的。也就是，信息论可用于估计，但是也有可能会出错。以4为例，信息熵为3，3/1.58并向上取整，信息论表示答案为2 ，但事实上是分不出来的。

三进制正逆序

特点

1. 稍显抽象
2. 可以知道具体操作过程
3. 答案准确

感谢知乎大佬，详见顶部原文，有论文和实现。

此处给出网页可视化实现及算法流程介绍

但是需要注意的是，不同浏览器显示不同，笔者用的是火狐浏览器，评论里有用谷歌浏览器的，都出现了12个球需要4次操作的情况，原文作者有介绍，是因为浏览器的精度计算问题。据其他评论者说，手机浏览器可以正常显示12个球三次操作，笔者自己实验的时候，使用了老版edge浏览器（不是新版，新版换了内核，也可能出现这个情况），可以正常展示12个球3次操作。

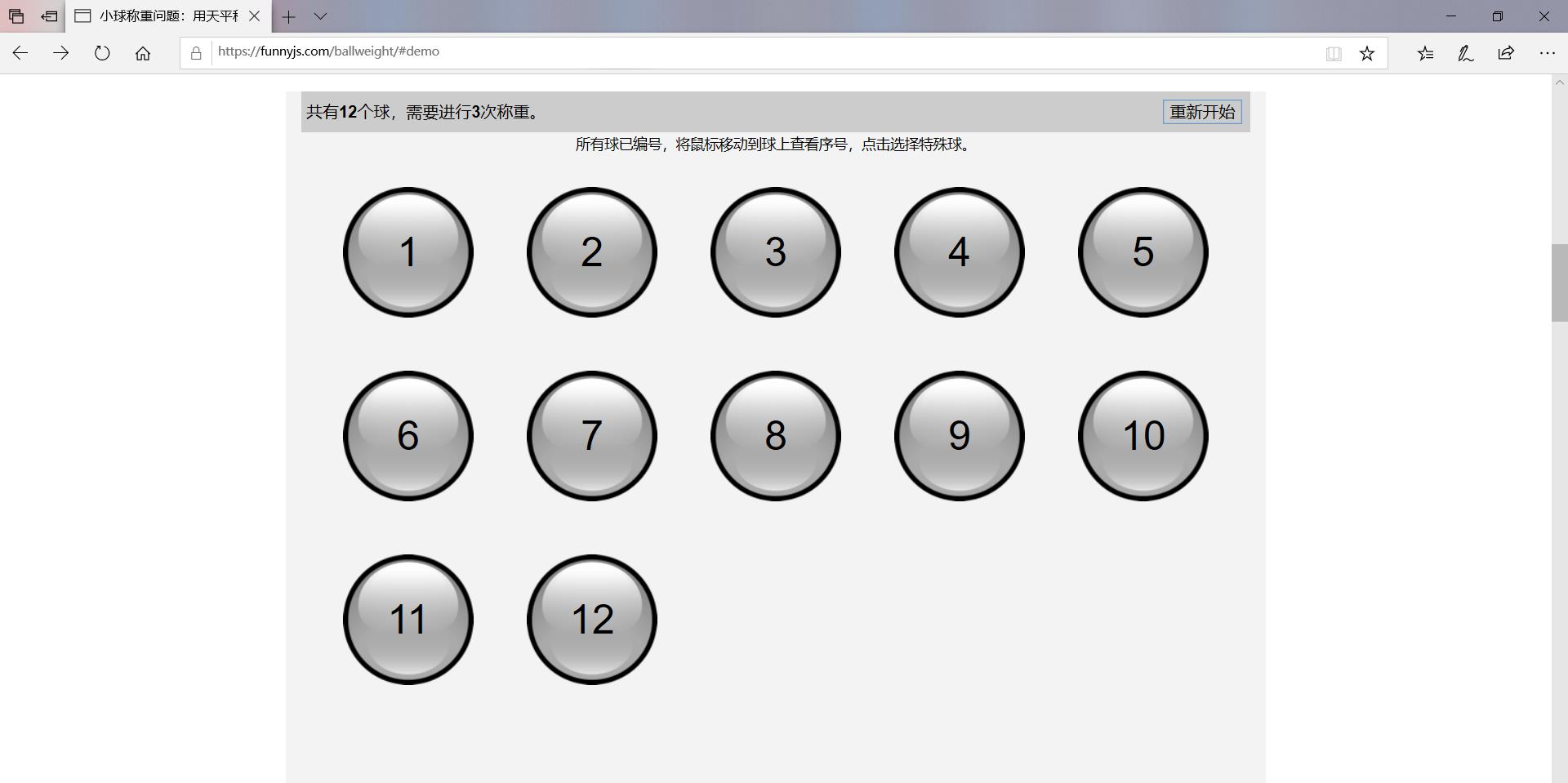
三进制正逆序算法原理是，

1. 给每个球编号，编号原则为使用log(N*2+3)/log(3) 向上取整的数目的位数，构建3进制编号。
2. 每个球都有正序号和逆序号，编号的每一位代表每次操作他所在的位置，0-小于，1-平衡，2-大于
3. 第k次操作将所有的小球正序编号第k位三进制取出，0放在天平左边，2放在天平右边，1不放，如果左偏则记录为0，有偏记录为2，无偏记录为1.
4. 将记录的编号与所有小球进行比较，如果和某个小球的正序一样，则这个小球比其它球重，如果和某个小球的逆序一样，则这个小球比其它球轻。

方法十分巧妙，当时也理解了很久，相当于这些小球的编号就是操作，如果每次操作都有他，最后一定是他。

快速排序

特点

1. 依托快速排序

关于这个看了个大概，大概就是和快排思路类似，可知其交换次数为log(n)。具体还不太懂，以后有机会再更新。但是快排本质上也是在平衡每次操作之后的概率，和信息论有异曲同工之处。

决策树

可以利用离散数学中决策树的思想来解决问题，n将是决策树的根。在本题中，由于每次称重会有三种结果，分别是左边轻、右边轻、以及相等，因此题中的决策树将是一个三叉树。在n = 999的情况下称重的结果就是log3 999的上界，答案是7次。同样的道理也可以用在以两两对比为基础的排序算法的次数上，即对一个长度为n的数组进行排序的次数就是log2 n。

作者：谢坤
链接：https://www.zhihu.com/question/20854512/answer/95109354
来源：知乎

这个也不是特别懂，先记录。

矩阵

参考链接

递归

特点

1. 数学性强
2. 可以知道操作方式

原文已经写的很好了，此处转载他的图片。
首先是有一个引理。

在 $3^k$个球中已知一个球偏重（偏轻同理），需要k次称量把它找出来。

下面证明需要反复使用引理。

作者：Ecthelion
链接：https://www.zhihu.com/question/20854512/answer/959690337
来源：知乎

先把球分成三堆。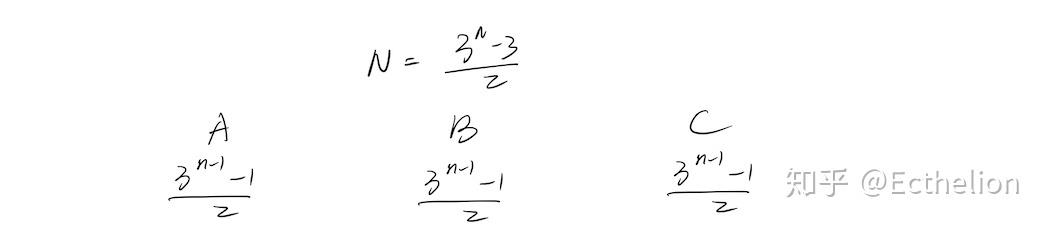每一堆可以细分成n-1小堆。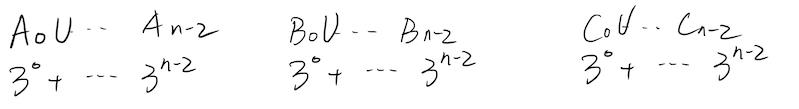然后第一次称量。（WLOG：不失一般的）第二次。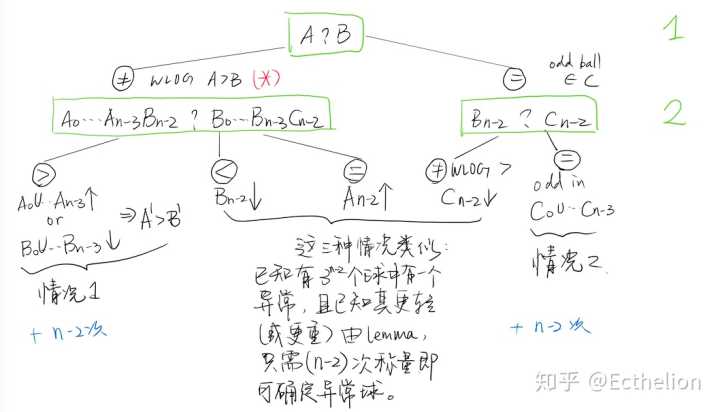注意到情况1和（*）处的相似性！然后我们就可以用迭代算一下：中间三个分支实际上就是Lemma中k=n-2的情况，都需要n-2次称量。最右边的情况2，和”异常球在C中“是相似的，我们也可以用迭代算一下：得知情况二也需要n-2次称量。结论是：n次称量找出 个球中异常球并判断偏轻/偏重。

我觉得可以说是十分巧妙了，当时也想要用递归去写，但是却没有想到该怎么写。