[code] PTA 胡凡算法笔记 DAY044

Posted 2022-12-03 wait_for_that_day5

文章目录

• • 题目 A1088 Rational Arithmetic
  • 小结

题目 A1088 Rational Arithmetic

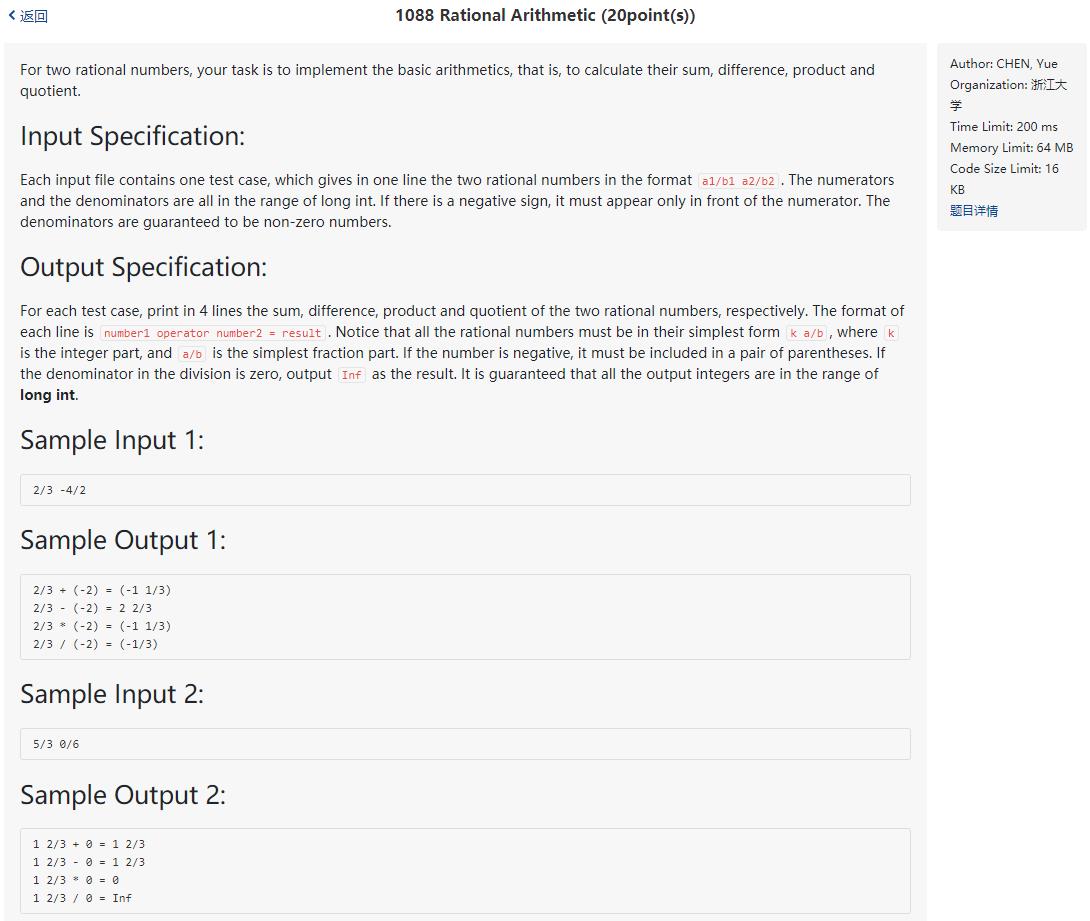
• 题意
  输入两个分数，输出进行加减乘除的结果，需要输出最简的方式（带分数或整数或真分数）。除法分母为0时，输出Inf。

• 思路
  数据用结构体的方式存储，主要是对数据的化简和输出真分数函数的书写。然后这里还需要注意一下除法分母为0时需要单独处理。然后设计四则运算函数的时候要考虑清楚哪些是函数外控制的哪些是函数内控制的。

• Code in C++

#include <cstdio>
#include <algorithm>

struct fraction

    long long up;
    long long down;
    void print()
    
        printf("%lld / %lld\\n", up, down);
    
a, b;

// 最大公约数
long long gcd(long long a, long long b);
// 化简
fraction reduction(fraction f);
fraction add(fraction a, fraction b);
fraction sub(fraction a, fraction b);
fraction mul(fraction a, fraction b);
fraction divide(fraction a, fraction b);
void print(fraction a);

int main()

    scanf("%lld/%lld %lld/%lld", &a.up, &a.down, &b.up, &b.down);
    // 加
    print(a);
    printf(" + ");
    print(b);
    printf(" = ");
    print(add(a, b));
    printf("\\n");
    // 减
    print(a);
    printf(" - ");
    print(b);
    printf(" = ");
    print(sub(a, b));
    printf("\\n");

    // 乘
    print(a);
    printf(" * ");
    print(b);
    printf(" = ");
    print(mul(a, b));
    printf("\\n");

    // 除
    print(a);
    printf(" / ");
    print(b);
    printf(" = ");
    if (b.up == 0) printf("Inf");
    else print(divide(a, b));

    return 0;


long long gcd(long long a, long long b)

    if (b == 0) return a;
    else return gcd(b, a % b);


fraction reduction(fraction f)

    if (f.down < 0)
    
        f.up = -f.up;
        f.down = -f.down;
    
    if (f.up == 0) f.down = 1;
    else
    
        long long gcd_num = gcd(std::abs(f.up), std::abs(f.down));
        f.up = f.up / gcd_num;
        f.down = f.down / gcd_num;
    

    return f;


fraction add(fraction a, fraction b)

    fraction result;
    result.up = a.up * b.down + b.up * a.down;
    result.down = a.down * b.down;
    return reduction(result);


fraction sub(fraction a, fraction b)

    fraction result;
    result.up = a.up * b.down - b.up * a.down;
    result.down = a.down * b.down;
    return reduction(result);


fraction mul(fraction a, fraction b)

    fraction result;
    result.up = a.up * b.up;
    result.down = a.down * b.down;
    return reduction(result);


fraction divide(fraction a, fraction b)

    fraction result;
    result.up = a.up * b.down;
    result.down = a.down * b.up;
    return reduction(result);


void print(fraction a)

    a = reduction(a);
    if (a.up < 0) printf("(");
    // 整数
    if (a.down == 1) printf("%lld", a.up);
    // 假分数
    else if (std::abs(a.up) > a.down) printf("%lld %lld/%lld", a.up / a.down, std::abs(a.up) % a.down, a.down);
    // 真分数
    else printf("%lld/%lld", a.up, a.down);
    if (a.up < 0) printf(")");

---

小结

• 最大公约数的写法

• 约分操作

• 化简操作