SORT+DeepSORT

Posted 2022-12-03 Arrow

SORT+DeepSORT

• 1. 简介
• • 1.1 评价指标
  • 1.2 SORT功能
  • 1.3 DeepSORT功能
  • 1.4 实现方案
• 2. 卡尔曼滤波（Kalman Filter: 运动预测）
• 3. 匈牙利算法（Hungarian Algorithm:数据关联）
• • 3.1 分配问题（Assignment Problem）
  • 3.2 匈牙利算法（又叫KM算法）
  • • 3.2.1 算法步骤（假设矩阵为NxN方阵）
    • 3.2.2 程序实现
    • 3.2.3 KM算法在DeepSORT中的应用
• 4. SORT
• • 4.1 估计模型
  • 4.2 数据关联
• 5. DeepSORT
• • 5.1 跟踪处理和状态估计
  • 5.2 分配问题
  • • 5.2.1 运动信息（motion information）
    • 5.2.2 外观信息（appearance information）
    • 5.2.3 组合运动和外观信息
    • 5.2.4 级联匹配
  • 5.3 DeepSORT工作流程
  • • 5.3.1 检测
    • 5.3.2 生成Detections
    • 5.3.3 卡尔曼滤波预测阶段
    • 5.3.4 匹配
    • 5.3.5 卡尔曼滤波更新阶段

1. 简介

• SORT: Simple Online and Realtime Tracking
• MOT：Multiple Object Tracking (是一个数据关联问题)
• BBox：Bounding Box
• ReID：Re-Identification
• MOTA：Multi-object tracking accuracy
• MOTP：Multi-object tracking precision
• FP：number of false detections （误检数）
• FN：number of missed detections （漏检数）
• 奥卡姆剃刀定律（Occam’s Razor) ：“如无必要，勿增实体”，即“简单有效原理”

1.1 评价指标

• $(o_i,h_j)$：是对象$o_i$与跟踪假设$(h_j)$间的一个映射(匹配)，且它们的距离不超过阈值$T$，所有的映射应当确保所有的距离和最小
• $c_t$：在时间 $t$ ，找到的匹配数量
• $d_t^i$：在时间$t$，对象$o_i$与它的跟踪假设间的距离 (距离计算方法：区域（框）跟踪器，距离可用两者的重叠区域来度量；点跟踪器，距离可用两者中心点的欧氏距离来度量)
• $f{p}_t$：在时间$t$，未被匹配的跟踪假设数量（false positive）
• $m_t$：在时间$t$，未被匹配的对象数量（missed objects）
• $g_t$：在时间$t$，找到的对象数量
• $mm{e}_t$：在时间$t$，ID跳变数量
• MOTP：跟踪定位精度指标
  $$MOTP=\frac{{\Sigma }_{i,t}{d}_t^i}{{\Sigma }_t{c}_t}$$
• MOTA：综合了漏检率，误检率，以及 ID 跳变率
  $$MOTA=1-\frac{{\Sigma }_t(m_t+f{p}_t+mm{e}_t)}{{\Sigma }_t{g}_t}$$

1.2 SORT功能

• 仅使用Kalman Filter和Hungarian algorithm获得较好的准确率和实时性
  • 在图像空间执行卡尔曼滤波
  • 使用匈牙利算法进行相邻帧间的数据关联
• 遵循奥卡姆剃刀定律，未考虑以下因素：
  • 外观特征
  • 短期和长期的遮挡
  • 其速度模型仅考虑相邻帧间的预测，而未考虑对象重识别（ReID）
• 不足之外
  • 仅状态估计不确定性低时效果才比较好 (由所使用的关联指标决定的)

1.3 DeepSORT功能

• 方法：
  • 在SORT的基础上，集成了外观信息（appearance information）以改善SORT的性能
  • 在可视的外观空间中，通过最近邻查询方法（nearest neighbor queries）来建立测量到跟踪的关联（measurement-to-track associations）
• 效果：
  • 可跟踪长时间遮挡的对象
  • 有效地减少了ID跳变

1.4 实现方案

• 视频中不同时刻的同一个人，位置发生了变化，那么是如何关联上的呢？ 答案就是：
  • 匈牙利算法
  • 卡尔曼滤波。
• 卡尔曼滤波可以基于目标前一时刻的位置，来预测当前时刻的位置，并且可以比传感器（在目标跟踪中即目标检测器，比如Yolo等）更准确的估计目标的位置。
• 匈牙利算法可以告诉我们当前帧的某个目标，是否与前一帧的某个目标相同。

2. 卡尔曼滤波（Kalman Filter: 运动预测）

• 作用：基于传感器的测量值来更新预测值，以达到更精确的估计。
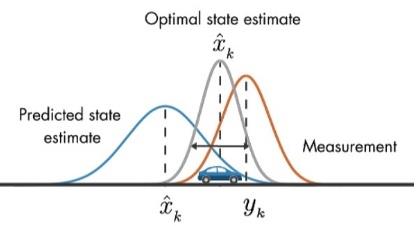
• 举例说明：假设我们要跟踪小车的位置变化，如下图所示，蓝色的分布是卡尔曼滤波预测值，棕色的分布是传感器的测量值，灰色的分布就是基于测量值更新后的最优估计值。
• 在目标跟踪中，需要估计track的以下两个状态：
  • 均值(Mean)：表示目标的位置信息，由BBox的中心坐标 $(c_x,c_y)$，宽高比r，高h，以及各自的速度变化值组成，由8维向量表示为 $x=[c_x,c_y,r,h,v_x,v_y,v_r,v_h]$，各个速度值初始化为0。
  • 协方差(Covariance )：表示目标位置信息的不确定性，由8x8的对角矩阵表示，矩阵中数字越大则表明不确定性越大，可以以任意值初始化。
• 卡尔曼滤波分为两个阶段：
  • (1) 预测track在下一时刻的位置
  • (2) 基于detection来更新预测的位置。

3. 匈牙利算法（Hungarian Algorithm:数据关联）

3.1 分配问题（Assignment Problem）

• 假设有N个人和N个任务，每个任务可以任意分配给不同的人，已知每个人完成每个任务要花费的代价不尽相同，那么如何分配可以使得总的代价最小。
• 举个例子，假设现在有3个任务，要分别分配给3个人，每个人完成各个任务所需代价矩阵（cost matrix）如下所示（这个代价可以是金钱、时间等等）
  $$\begin{array}{clcr}Person& \text{Task1}& \text{Task2}& \text{Task3}\\ Person1& 15& 40& 45\\ Person2& 20& 60& 35\\ Person3& 20& 40& 25\end{array}$$
• 怎样才能找到一个最优分配，使得完成所有任务花费的代价最小呢？

3.2 匈牙利算法（又叫KM算法）

• 匈牙利算法：就是用来解决分配问题的一种方法，它基于定理：如果代价矩阵的某一行或某一列同时加上或减去某个数，则这个新的代价矩阵的最优分配仍然是原代价矩阵的最优分配

3.2.1 算法步骤（假设矩阵为NxN方阵）

1. 对于矩阵的每一行，减去其中最小的元素
2. 对于矩阵的每一列，减去其中最小的元素
3. 用最少的水平线或垂直线覆盖矩阵中所有的0
4. 如果线的数量等于N，则找到了最优分配，算法结束，否则进入步骤5
5. 找到没有被任何线覆盖的最小元素，每个没被线覆盖的行减去这个元素，每个被线覆盖的列加上这个元素，返回步骤3

• step1 每一行最小的元素分别为15、20、20，减去得到：
  $$\begin{array}{clcr}Person& \text{Task1}& \text{Task2}& \text{Task3}\\ Person1& 0& 25& 30\\ Person2& 0& 40& 15\\ Person3& 0& 20& 5\end{array}$$

• step2 每一列最小的元素分别为0、20、5，减去得到：
  P e r s o n Task1 Task2 Task3 P e r s o n 1 0 5 25 P e r s o n 2 0 20 10 P e r s o n 3 0 0 0 \\beginarrayc|lcr Person & \\textTask1 & \\textTask2 & \\textTask3 \\\\ \\hline Person1 & 0 & 5 & 25 \\\\ Person2 & 0 & 20 & 10 \\\\ Person3 & 0 & 0 & 0 \\endarray

  以上是关于SORT+DeepSORT的主要内容，如果未能解决你的问题，请参考以下文章

  SORT+DeepSORT

  技术分享 吊舱目标追踪---deepsort原理讲解

  DeepSort目标跟踪算法

  DeepSort：论文翻译

  基于yolov5与Deep Sort的流量统计与轨迹跟踪

  多目标跟踪(MOT)--DeepSort原理及代码详解