《Feature-metric Loss for Self-supervised Learning of Depth and Egomotion》论文笔记

Posted 2022-12-03 m_buddy

参考代码：FeatDepth

1. 概述

介绍：在自监督深度估计中以光度重构误差作为损失函数，需要计算的是每个像素点的对应差异，但是在一些无/弱纹理或是存在多个最小值的低辨识度像素，区域光度重构误差就会产生错误匹配结果。对此，这篇文章提出了一种新的重建误差度量FeatureMetric loss，也就是在feature map的维度计算loss，从而去约束重建的过程。那么怎么去生成满足要求的feature map呢？一个自然的办法便是使用自编码网络去重建输入彩色图像（也是一个自监督任务），而且还需要在feature map上做一阶和二阶梯度约束使得其满足自监督深度估计收敛条件。

在自监督深度估计任务中是以光度重构误差作为损失，但是光度重构误差最小时却不一定代表真实深度误差最小，特别是在无纹理区域上，这样的约束经常导致错误的深度估计结果。同时为了减少深度预测错误带来的不连续问题，通常会引入平滑约束，这样会导致在一些深度平面交汇处出现模糊的情况。为了使得重构误差中的单个像素更加具有辨别能力，文章提出了feature metric loss，也就是在特征图的维度实现重建最小化。其中运用到的特征图提取网络来自于自监督的自编码器。除了自编码器使用的重建损失外，还使用了discriminative loss和convergent loss，分别用于生成更具分辨能力的单像素表达以及减少像素之间的方差。

下图展示了MonoDepth2和文章方法的比较，这篇文章的方法效果更好：

2. 方法设计

2.1 pipeline结构

文章的整体pipeline见下图所示：

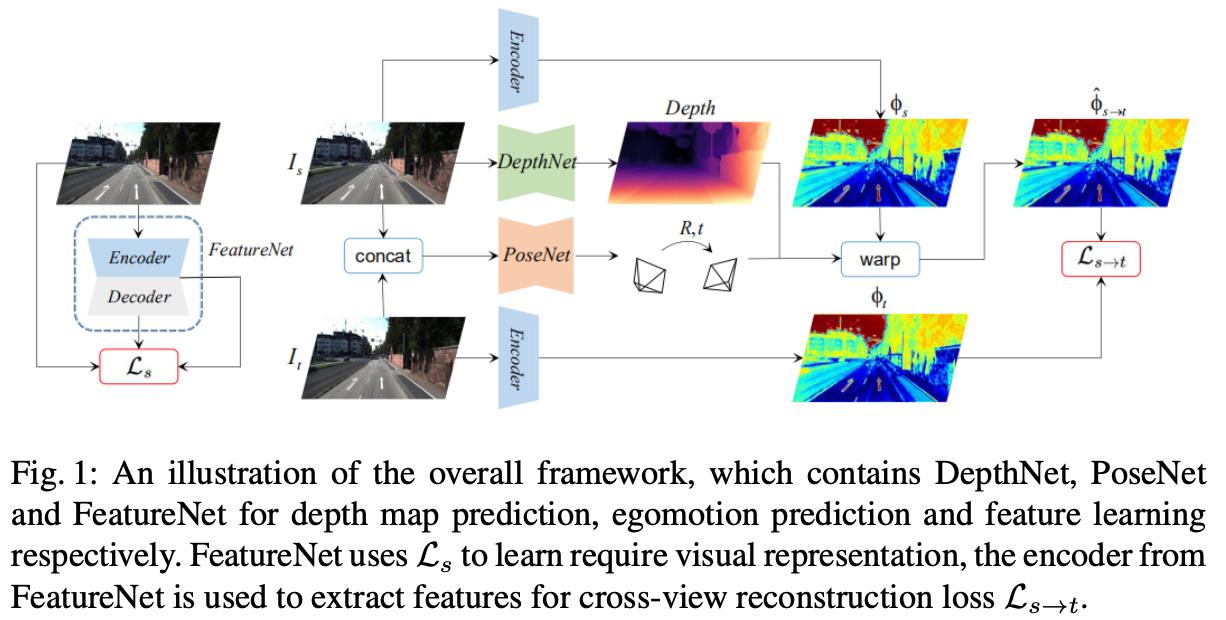
在上图的左边是用于训练自编码器的网络，其编码器会用于后面单目自监督估计中特征图的抽取。右边就是标准的单目自监督深度估计的pipeline了。

2.2 自编码器

这里使用的自编码器训练是采取自监督的形式进行的，在其训练过程中包含3个部分的损失：图像重建损失、discriminative loss和convergent loss。

图像重建损失： 这部分是直接用于自编码器生成和原图一致的结果：
$$L_{rec}\sum _p|I(p)-I_{rec}(p){|}_1$$
discriminative loss： 这部分用于激励每个像素生成更具判别能力的信息表达，特别是用于区分无纹理区域的像素，因而会激励网络在这些区域产生更多的梯度
$$L_{dis}=-\sum _p|{\nabla }^1\varphi (p){|}_1$$
convergent loss： 该损失函数用于对特征图上的梯度平滑，因而保证特征图梯度的连续性和较大的收敛半径
$$L_{cvt}=\sum _p|{\nabla }^2\varphi (p){|}_1$$
对于上述中的${\nabla }^1={\partial }_x+{\partial }_y,{\nabla }^2={\partial }_{xx}+2{\partial }_{xy}+{\partial }_{yy}$。则整体的自编码器自监督损失函数描述为：
$$L_s=L_{rec}+\alpha L_{dis}+\beta L_{cvt}$$
其中， $\alpha =\beta =1e-3$。那么更进一步上述中的几个loss对网络的整体性能影响见下表：

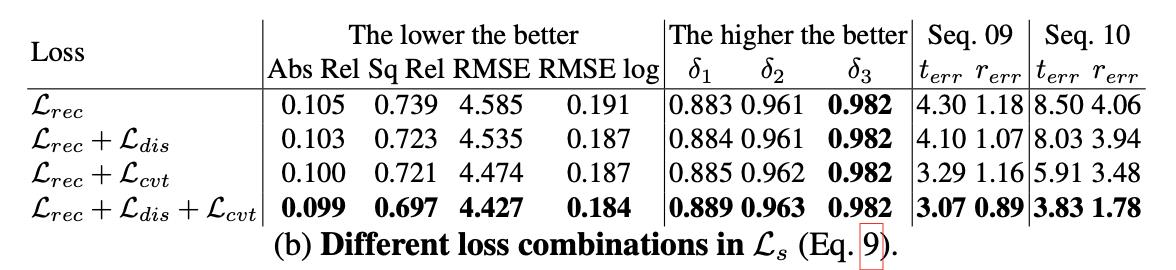
2.3 深度估计约束

这里将自编码器中的编码器引入到深度估计网络中去，因而除了直接在图片维度进行光度重构误差，还在feature map的维度进行重构误差最小化。则深度自监督部分的损失函数描述为：
$$L_{s\to t}=\sum _p{L}_{fm}({\varphi }_s(\hat{p}),{\varphi }_t(p))+\sum _p{L}_{ph}(I_s(\hat{p}),I_t(p))$$
其中，前面的一项便是feature map上的重构误差，后面一项就是光度重构误差。对于feature map上的重构误差这里用L1范数的形式进行表示：
$$L_{fm}=|{\varphi }_s(\hat{p}),\varphi (I_t(p)){|}_1$$
对于图像维度的光度重构误差描述为：
$$L_{ph}=0.15\sum _p|I_s(\hat{p})-I_t(p){|}_1+0.85\frac{1-SSIM(I_s(\hat{p}),I_t(p))}{2}$$
而在实际运算过程中也会考虑遮挡的情况，这里跟Monodepth2中的处理机制一样，采取的是选择重构误差作为该点损失的形式：
$$L_{s\to t}^{{}^{\prime }}\sum _p\underset{s\in V}{\min }{L}_{s\to t}({\varphi }_s(\hat{p}),{\varphi }_t(p))$$
因而，结合上述中的自编码器损失，总体损失描述为：
$$L_{total}=以上是关于《Feature-metric\; Loss\; for\; Self-supervised\; Learning\; of\; Depth\; and\; Egomotion》论文笔记的主要内容，如果未能解决你的问题，请参考以下文章$$

Paper Reading - Loss系列 - Focal Loss for Dense Object Detection

[论文理解]Focal Loss for Dense Object Detection（Retina Net）

RuntimeError: _thnn_nll_loss_forward not supported on CUDAType for Long

focal loss for multi-class classification

Focal Loss for Dense Object Detection 论文阅读

“nll_loss_forward_reduce_cuda_kernel_2d_index“ not implemented for ‘Float‘