基于arx模型的MPC预测控制器simulink建模与仿真实现

Posted 2022-12-02 fpga和matlab

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

MPC的优点
模型预测控制善于处理多输入多输出系统
       对于MIMO系统，PID需要为每个子系统单独设计PID控制器，由于存在耦合对于较大的系统难以实现
1.MPC控制器可以较好控制MIMO系统

2.模型预测控制可以处理约束，安全性约束，上下阈值
3.模型预测控制是有向前考虑未来时间步的有限时域优化（一定的预测能力）最优控制要求在整个时间优化实际上模型预测控制采用了一个折中的策略，既不是像最优控制那样考虑这个时域，也不是完全的贪婪控制仅仅考虑当前，而是考虑未来的有限时间域。

　    在当今过程控制中，PID当然是用的最多的控制方法，但MPC也超过了10%的占有率。MPC是一个总称，有着各种各样的算法。其动态矩阵控制（DMC）是代表作。DMC采用的是系统的阶跃响应曲线，其突出的特点是解决了约束控制问题。那么是DMC是怎么解决约束的呢？在这里只给出宏观的解释，而不做详细的说明。DMC把线性规划和控制问题结合起来，用线性规划解决输出约束的问题，同时解决了静态最优的问题，一石二鸟，在工业界取得了极大的成功。

2.作用机理
　　MPC作用机理描述为：在每一个采用时刻，根据获得的当前测量信息，在线求解一个有限时间开环优化问题，并将得到的控制序列的第一个元素作用于被控对象。在下一个采样时刻，重复上述过程：用新的测量值作为此时预测系统未来动态的初始条件，刷新优化问题并重新求解 。
即MPC算法包括三个步骤：
（1）预测系统未来动态；
（2）（数值）求解开环优化问题；
（3）将优化解的第一个元素（或者说第一部分）作用于系统
　　这三步是在每个采样时刻重复进行的，且无论采用什么样的模型，每个采样时刻得到的测量值都作为当前时刻预测系统未来动态的初始条件

大致的模型建立如下所示：

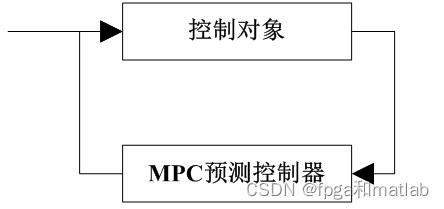
 其中MPC预测控制器，采用ARX模型进行设计。其内部结构框图如下所示：

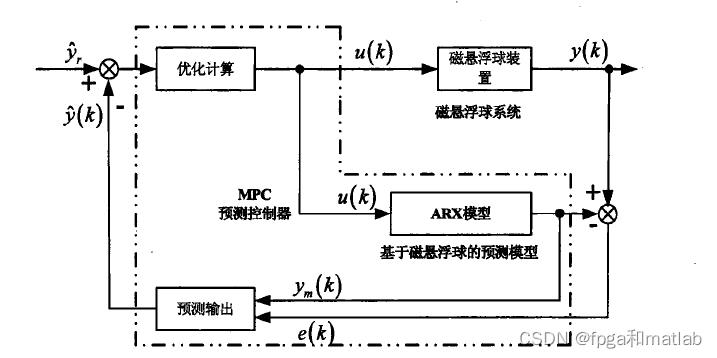
这里虚线部分，就是MPC预测控制器，使用S函数进行设计。

相关公式如下所示：

二、核心程序

下面，就根据上面的结构框图进行系统的simulink建模以及相关S函数的编程实现。

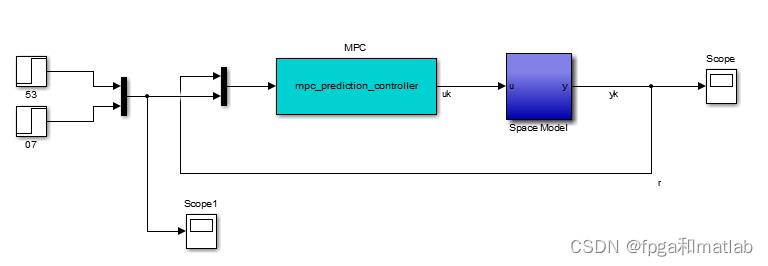
主要是MPC预测控制器的设计，根据论文的结构框图，MPC由三个部分构成，即

优化计算，

ARX模型

预测输出

function Output = mpc_pcontroller(A_state,...
                                  B_state,...
                                  C_state,...
                                  D_state,...
                                  p_cs,...
                                  m_cs,...
                                  Q_cs,...
                                  R_cs)

[Rm,Cn] = size(D_state);

%MPC优化计算
[ak,bk] = Predict_mpc(A_state,...
                      B_state,...
                      C_state,...
                      D_state,...
                      Cn,...
                      p_cs,...
                      m_cs,...
                      Q_cs,...
                      R_cs);
 
x0 = zeros(size(A_state,1),1);
u0 = zeros(Cn,1);
 

%预测输出
Output = @MPC_pred;

function Output = MPC_pred(din,Ref)
    %状态更新
    x0 = A_state * x0 + B_state * u0;

    if size(Ref,2) < p_cs
       ref = [Ref Ref(:,end + zeros(p_cs-size(Ref,2),1))];
    else
       ref = Ref(:,1:p_cs);
    end

    %计算误差
    Error  = abs(din(:) - C_state*x0);

    %ARX模型
    y1     = -x0;
    u1     =  reshape(ref-Error(:,ones(p_cs,1)),[],1);
    
    %第一路的输出
    ua     = sum(ak(1,:) * y1) + sum(bk(1,:) * u1);
    %第二路的输出
    ub     = sum(ak(2,:) * y1) + sum(bk(2,:) * u1);
    
    u0     =[ua;ub];
    %控制器输出 
    Output = u0;
end

end

%MPC优化计算
function [Ak,Bk] = Predict_mpc(A_state,...
                               B_state,...
                               C_state,...
                               D_state,...
                               Ls2,...
                               p_cs,...
                               m_cs,...
                               Q_cs,...
                               R_cs);
 
[R1,C1]      = size(B_state);
R2           = size(C_state,1);
%根据状态值，获得公式中的G变量
[G1,G2]      = func_G_cal(A_state,B_state,C_state,D_state,R1,R2,C1,m_cs,p_cs);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义预测矩阵
[P1,P2,P3,L] = func_predict_Matrix(R1,R2,C1,p_cs,A_state,B_state,C_state);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 
%计算控制系数
[K1,K2]      = func_K_cal(G2,P2,P3,L,R2,C1,p_cs,m_cs,Q_cs,R_cs);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%输出a和b系数
Ak       = K1(1:Ls2,:);
Bk       = K2(1:Ls2,:);
end

三、测试结果

仿真结果如下所示：

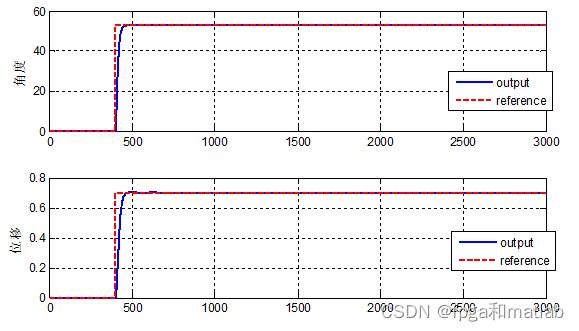
 上述的仿真结果，表面本文所研究的MPC预测控制器具有更好的控制性能。

A08-46