算法基础堆排序——O(nlogn)
Posted 胡毛毛_三月
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法基础堆排序——O(nlogn)相关的知识,希望对你有一定的参考价值。
堆排序
数组、链表都是一维的数据结构,相对来说比较容易理解,而堆是二维的数据结构,对抽象思维的要求更高,所以许多程序员「谈堆色变」。但堆又是数据结构进阶必经的一步,我们不妨静下心来,将其梳理清楚。
堆:符合以下两个条件之一的完全二叉树:
- 根节点的值 ≥ 子节点的值,这样的堆被称之为最大堆,或大顶堆;
- 根节点的值 ≤ 子节点的值,这样的堆被称之为最小堆,或小顶堆。

为了有一个轻松的开场,我们先来看一个程序员的段子放松一下:
你有哪些用计算机技能解决生活问题的经历?
我认识一个大牛,他不喜欢洗袜子,又不喜欢袜子的臭味。于是他买了很多样式一样的袜子,把这些袜子放在地上,根据臭的程度,摆一个二叉堆。每天早上,他 pop 两只最“香”的袜子,穿上;晚上回到家,把袜子脱下来,push 到堆里。某一天,top 的袜子超过他的耐臭能力,全扔掉,买新的。
如果我们将袜子 「臭的程度」 量化,这位大牛每天做的事情就是构建一个大顶堆,然后将堆顶的袜子取出来。再调整剩下的袜子,构建出一个新的大顶堆,再次取出堆顶的袜子。这个过程使用的就是堆排序的思想,它是由 J. W. J. Williams 在 1964 年发明的。
堆排序过程如下:
-
用数列构建出一个大顶堆,取出堆顶的数字;
-
调整剩余的数字,构建出新的大顶堆,再次取出堆顶的数字;
-
循环往复,完成整个排序。
整体的思路就是这么简单,我们需要解决的问题有两个:
- 如何用数列构建出一个大顶堆;
- 取出堆顶的数字后,如何将剩余的数字调整成新的大顶堆。
构建大顶堆 & 调整堆
构建大顶堆有两种方式:
- 方案一:从
0开始,将每个数字依次插入堆中,一边插入,一边调整堆的结构,使其满足大顶堆的要求; - 方案二:将整个数列的初始状态视作一棵完全二叉树,自底向上调整树的结构,使其满足大顶堆的要求。
方案二更为常用,动图演示如下:
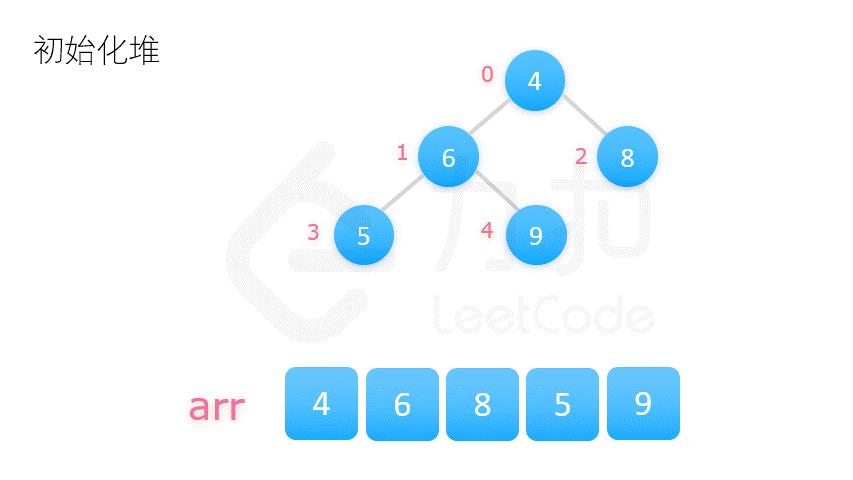

在介绍堆排序具体实现之前,我们先要了解完全二叉树的几个性质。将根节点的下标视为 0,则完全二叉树有如下性质:
-
对于完全二叉树中的第
i个数,它的左子节点下标:left = 2i + 1 -
对于完全二叉树中的第
i个数,它的右子节点下标:right = left + 1 -
对于有
n个元素的完全二叉树(n≥2)(n≥2),它的最后一个非叶子结点的下标:n/2 - 1
堆排序代码如下:
public static void heapSort(int[] arr)
// 构建初始大顶堆
buildMaxHeap(arr);
for (int i = arr.length - 1; i > 0; i--)
// 将最大值交换到数组最后
swap(arr, 0, i);
// 调整剩余数组,使其满足大顶堆
maxHeapify(arr, 0, i);
// 构建初始大顶堆
private static void buildMaxHeap(int[] arr)
// 从最后一个非叶子结点开始调整大顶堆,最后一个非叶子结点的下标就是 arr.length / 2-1
for (int i = arr.length / 2 - 1; i >= 0; i--)
maxHeapify(arr, i, arr.length);
// 调整大顶堆,第三个参数表示剩余未排序的数字的数量,也就是剩余堆的大小
private static void maxHeapify(int[] arr, int i, int heapSize)
// 左子结点下标
int l = 2 * i + 1;
// 右子结点下标
int r = l + 1;
// 记录根结点、左子树结点、右子树结点三者中的最大值下标
int largest = i;
// 与左子树结点比较
if (l < heapSize && arr[l] > arr[largest])
largest = l;
// 与右子树结点比较
if (r < heapSize && arr[r] > arr[largest])
largest = r;
if (largest != i)
// 将最大值交换为根结点
swap(arr, i, largest);
// 再次调整交换数字后的大顶堆
maxHeapify(arr, largest, heapSize);
private static void swap(int[] arr, int i, int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
尚硅谷:
package 排序;
import java.util.Arrays;
import 练习本.a;
public class 堆排序
/**
* 1.无序序列构建成一个堆,根据升序降序需求选择大腚堆或小顶堆
* 2.将堆顶元素与末尾元素交换,将最大元素“沉”到数组末端
* 3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到这个序列有序
* */
public static void main(String[] args)
// TODO Auto-generated method stub
// 要求将数组进行升序排序
int arr[] = 4,6,8,5,9;
heapSort(arr);
// 编写一个堆排序的方法
public static void heapSort(int arr[])
int temp = 0;
// 分步完成
// adjustHeap(arr, 1, arr.length);
// System.err.println("第一次调整"+Arrays.toString(arr)); // 4,9,8,5,6
// adjustHeap(arr, 0,arr.length);
// System.err.println("第一次调整"+Arrays.toString(arr)); // 9, 6, 8, 5, 4
/**
* 1.无序序列构建成一个堆,根据升序降序需求选择大腚堆或小顶堆
* */
for(int i = arr.length / 2 -1; i >=0; i--)
adjustHeap(arr, i, arr.length);
/**
*2.将堆顶元素与末尾元素交换,将最大元素“沉”到数组末端
*3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到这个序列有序
* */
for (int j = arr.length-1;j>0;j--)
// 交换
swap(arr, 0, j);
// 调整
adjustHeap(arr, 0, j);
System.out.println("数组="+Arrays.toString(arr));
// 将一个数组(二叉树),调整成一个大顶堆
/**
* 1.无序序列构建成一个堆,根据升序降序需求选择大腚堆或小顶堆
* 功能:完成 将 以 i对应的非叶子结点的树调整成大顶堆
* 例: int arr[] = 4,6,8,5,9;
* i = 1,adjustHeap=>4,9,8,5,6
* i = 0,adjustHeap=>9,4,8,5,6
* =>9,6,8,5,4
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整,length是在逐渐减少的
* */
public static void adjustHeap(int arr[],int i,int length)
int temp = arr[i]; // 先取出当前元素的值,保存在临时变量
// 开始调整
// 说明:k = 2*i+1 是 i 的左子结点
for (int k = 2*i+1; k < length; k=k*2+1)
if (k+1 < length && arr[k]<arr[k+1])
k++;
if (arr[k]>temp)
arr[i] = arr[k];
i = k;
else
break;
// 当for循环结束后,我们已经将以i为父结点的树的最大值,放在了最顶(以i为父结点的局部二叉树)
arr[i] = temp;
// 交换函数
public static void swap(int arr[],int i,int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
堆排序的第一步就是构建大顶堆,对应代码中的 buildMaxHeap 函数。我们将数组视作一颗完全二叉树,从它的最后一个非叶子结点开始,调整此结点和其左右子树,使这三个数字构成一个大顶堆。
调整过程由 maxHeapify 函数处理, maxHeapify 函数记录了最大值的下标,根结点和其左右子树结点在经过比较之后,将最大值交换到根结点位置。这样,这三个数字就构成了一个大顶堆。
需要注意的是,如果根结点和左右子树结点任何一个数字发生了交换,则还需要保证调整后的子树仍然是大顶堆,所以子树会执行一个递归的调整过程。
这里的递归比较难理解,我们打个比方:构建大顶堆的过程就是一堆数字比赛谁更大。比赛过程分为初赛、复赛、决赛,每场比赛都是三人参加。但不是所有人都会参加初赛,只有叶子结点和第一批非叶子结点会进行三人组初赛。初赛的冠军站到三人组的根结点位置,然后继续参加后面的复赛。
而有的人生来就在上层,比如李小胖,它出生在数列的第一个位置上,是二叉树的根结点,当其他结点进行初赛、复赛时,它就静静躺在根结点的位置等一场决赛。
当王大强和张壮壮,经历了重重比拼来到了李小胖的左右子树结点位置。他们三个人开始决赛。王大强和张壮壮是靠实打实的实力打上来的,他们已经确认过自己是小组最强。而李小胖之前一直躺在这里等决赛。如果李小胖赢了他们两个,说明李小胖是所有小组里最强的,毋庸置疑,他可以继续坐在冠军宝座。
但李小胖如果输给了其中任何一个人,比如输给了王大强。王大强会和张壮壮对决,选出本次构建大顶堆的冠军。但李小胖能够坐享其成获得第三名吗?生活中或许会有这样的黑幕,但程序不会欺骗我们。李小胖跌落神坛之后,就要从王大强的打拼路线回去,继续向下比较,找到自己真正实力所在的真实位置。这就是 maxHeapify 中会继续递归调用 maxHeapify 的原因。
当构建出大顶堆之后,就要把冠军交换到数列最后,深藏功与名。来到冠军宝座的新人又要和李小胖一样,开始向下比较,找到自己的真实位置,使得剩下的 n−1n - 1 个数字构建成新的大顶堆。这就是 heapSort 方法的 for 循环中,调用 maxHeapify 的原因。
变量 heapSize 用来记录还剩下多少个数字没有排序完成,每当交换了一个堆顶的数字,heapSize 就会减 11。在 maxHeapify 方法中,使用 heapSize 来限制剩下的选手,不要和已经躺在数组最后,当过冠军的人比较,免得被暴揍。
这就是堆排序的思想。学习时我们采用的是最简单的代码实现,在熟练掌握了之后我们就可以加一些小技巧以获得更高的效率。比如我们知道计算机采用二进制来存储数据,数字左移一位表示乘以 22,右移一位表示除以 22。所以堆排序代码中的arr.length / 2 - 1 可以修改为 (arr.length >> 1) - 1,左子结点下标2 * i + 1可以修改为(i << 1) + 1。需要注意的是,位运算符的优先级比加减运算的优先级低,所以必须给位运算过程加上括号。
注:在有的文章中,作者将堆的根节点下标视为 11,这样做的好处是使得第 i 个结点的左子结点下标为 2i,右子结点下标为 2i + 1,与 2i + 1 和 2i + 2 相比,计算量会少一点,本文未采取这种实现,但两种实现思路的核心思想都是一致的。
分析可知,堆排序是不稳定的排序算法。
时间复杂度 & 空间复杂度
堆排序分为两个阶段:初始化建堆(buildMaxHeap)和重建堆(maxHeapify,直译为大顶堆化)。所以时间复杂度要从这两个方面分析。
根据数学运算可以推导出初始化建堆的时间复杂度为 O(n),重建堆的时间复杂度为 O(nlogn),所以堆排序总的时间复杂度为 O(nlogn)。推导过程较为复杂,故不再给出证明过程。
堆排序的空间复杂度为 O(1),只需要常数级的临时变量。
堆排序是一个优秀的排序算法,但是在实际应用中,快速排序的性能一般会优于堆排序。
练习
在选择排序小节,我们提到过,这种只需要部分排序的场景,非常适合用选择排序或堆排序来完成。因为他们的排序过程都是每次找出数组中的最大值(或最小值),依次将每个数字排好序。这两者之间,堆排序在性能上又比选择排序更好。
// 本题的解题思路是,先构建初始大顶堆,然后再将堆调整 k-1 次,此时,堆顶的元素就是第 k 个最大元素。
class Solution
public int findKthLargest(int[] nums, int k)
buildMaxHeap(nums);
// 调整 k-1 次
for (int i = nums.length - 1; i > nums.length - k; i--)
swap(nums, 0, i);
maxHeapify(nums, 0, i);
// 此时,堆顶的元素就是第 k 大的数
return nums[0];
// 构建初始大顶堆
public static void buildMaxHeap(int[] arr)
// 从最后一个非叶子结点开始调整大顶堆,最后一个非叶子结点的下标就是 arr.length / 2-1
for (int i = arr.length / 2 - 1; i >= 0; i--)
maxHeapify(arr, i, arr.length);
// 调整大顶堆,第三个参数表示剩余未排序的数字的数量,也就是剩余堆的大小
private static void maxHeapify(int[] arr, int i, int heapSize)
// 左子结点下标
int l = 2 * i + 1;
// 右子结点下标
int r = l + 1;
// 记录根结点、左子树结点、右子树结点三者中的最大值下标
int largest = i;
// 与左子树结点比较
if (l < heapSize && arr[l] > arr[largest])
largest = l;
// 与右子树结点比较
if (r < heapSize && arr[r] > arr[largest])
largest = r;
if (largest != i)
// 将最大值交换为根结点
swap(arr, i, largest);
// 再次调整交换数字后的大顶堆
maxHeapify(arr, largest, heapSize);
private static void swap(int[] arr, int i, int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
java堆排序:
class Solution
public static int findKthLargest(int[] nums, int k)
heapSort(nums);
return nums[nums.length-k];
// 编写一个堆排序的方法
public static void heapSort(int arr[])
int temp = 0;
// 分步完成
// adjustHeap(arr, 1, arr.length);
// System.err.println("第一次调整"+Arrays.toString(arr)); // 4,9,8,5,6
// adjustHeap(arr, 0,arr.length);
// System.err.println("第一次调整"+Arrays.toString(arr)); // 9, 6, 8, 5, 4
/**
* 1.无序序列构建成一个堆,根据升序降序需求选择大腚堆或小顶堆
* */
// 构造一个大顶堆
for(int i = arr.length / 2 -1; i >=0; i--)
adjustHeap(arr, i, arr.length);
/**
*2.将堆顶元素与末尾元素交换,将最大元素“沉”到数组末端
*3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到这个序列有序
* */
for (int j = arr.length-1;j>0;j--)
// 交换
swap(arr, 0, j);
// 调整
adjustHeap(arr, 0, j);
// System.out.println("数组="+Arrays.toString(arr));
// 将一个数组(二叉树),调整成一个大顶堆
public static void adjustHeap(int arr[],int i,int length)
int temp = arr[i]; // 先取出当前元素的值,保存在临时变量
// 开始调整
// 说明:k = 2*i+1 是 i 的左子结点
for (int k = 2*i+1; k < length; k=k*2+1)
if (k+1 < length && arr[k]<arr[k+1])
k++;
if (arr[k]>temp)
arr[i] = arr[k];
i = k;
else
break;
// 当for循环结束后,我们已经将以i为父结点的树的最大值,放在了最顶(以i为父结点的局部二叉树)
arr[i] = temp;
// 交换函数
public static void swap(int arr[],int i,int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
go堆排序:
func findKthLargest(nums []int, k int) int
HeapSort(nums)
return nums[len(nums)-k]
// 编写一个堆排序的方法
func HeapSort(arr []int) []int
/**
* 1.无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
* */
// 构造一个大顶堆
for i := len(arr)/2-1 ; i>=0;i--
adjustHeap(arr,i,len(arr))
/**
*2.将堆顶元素与末尾元素交换,将最大元素“沉”到数组末端
*3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到这个序列有序
* */
for j := len(arr)-1;j>0;j--
arr[0],arr[j] = arr[j],arr[0]
adjustHeap(arr,0,j)
return arr
// 将一个数组(二叉树),调整成一个大顶堆
func adjustHeap(arr []int,i int, length int)
temp := arr[i]; // // 先取出当前元素的值,保存在临时变量
// 开始调整
// 说明:k = 2*i+1 是 i 的左子结点
for k := 2*i+1;k < length; k = 2*k+1
if k+1< length && arr[k] < arr[k+1]
k++;
if arr[k] > temp
arr[i] = arr[k];
i = k;
else
break
// 当for循环结束后,我们已经将以i为父结点的树的最大值,放在了最顶(以i为父结点的局部二叉树)
arr[i] = temp
// 本题与上一题是类似的。
// 使用堆排序,先构建初始小顶堆,然后调整 k 次。此时数组末尾的 k 个元素组成的数组就是答案。
class Solution
public int[] getLeastNumbers(int[] arr, int k)
buildMinHeap(arr);
// 调整 k 次
for (int i = arr.length - 1; i > arr.length - k - 1; i--)
swap(arr, 0, i);
minHeapify(arr, 0, i);
// 取出 arr 末尾的 k 个元素
int[] result = new int[k];
System.arraycopy(arr, arr.length - k, result, 0, k);
return result;
// 构建初始小顶堆
private static void buildMinHeap(int[] arr)
// 从最后一个非叶子结点开始调整小顶堆,最后一个非叶子结点的下标就是 arr.length / 2-1
for (int i = arr.length / 2 - 1; i >= 0; i--)
minHeapify