单调栈应用——矩形最大面积问题

Posted 2022-11-27 白龙码~

LeetCode 84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

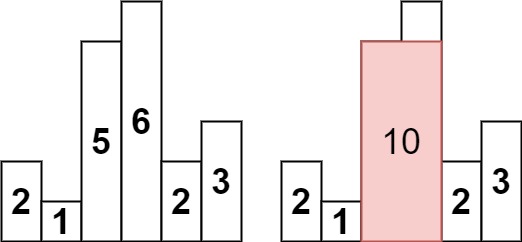
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

我们以每个柱子为观测对象：

如果第i根柱子的高度heights[i]是最大矩形的高，矩形的底是[L, R]，那么这意味着：heights[L...R]>=heights[i]，而heights[L-1]<heights[i], heights[R+1]<heights[i]。

因此，当我们确定某一根柱子为矩形的高时，只需要知道左边第一个矮于它的柱子下标L-1，右边第一个矮于它的柱子下标R+1，那么此时矩形的面积就等于(R-L+1)*heights[i]。

int largestRectangleArea(vector<int>& heights) 

    int n = heights.size();
    stack<int> st;
    vector<int> lmin(n); // 左边比heights[i]小的第一个柱子高度
    vector<int> rmin(n); // 右边比heights[i]小的第一个柱子高度
    for (int i = 0; i < n; ++i)
    
        while (!st.empty() && heights[i] <= heights[st.top()])
        
            st.pop();
        
        lmin[i] = st.empty() ? -1 : st.top();
        st.push(i);
    
    st = stack<int>();
    for (int i = n - 1; i >= 0; --i)
    
        while (!st.empty() && heights[i] <= heights[st.top()])
        
            st.pop();
        
        rmin[i] = st.empty() ? n : st.top();
        st.push(i);
    

    int res = 0;
    // L-1=rmin[i],R+1=rmin[i]，因此R-L+1=rmin[i] - lmin[i] - 1
    for (int i = 0; i < n; ++i)
    
        res = max(res, (rmin[i] - lmin[i] - 1) * heights[i]);
    
    return res;

---

LeetCode 85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

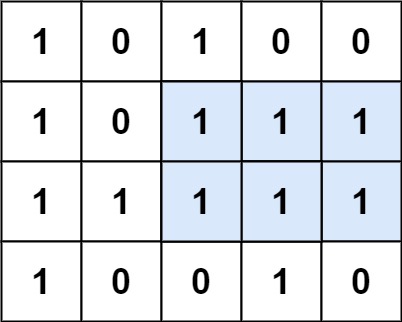
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

本题等价于上一题，只是我们需要柱状图预处理出来：

如果让第一层作为矩形的底所在层，那么柱状图如红色方框部分所示：

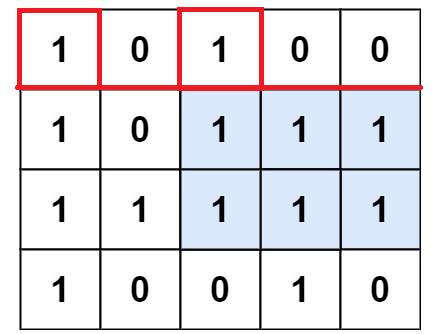
如果让第二层作为矩形的底所在层，那么柱状图如红色方框部分所示：

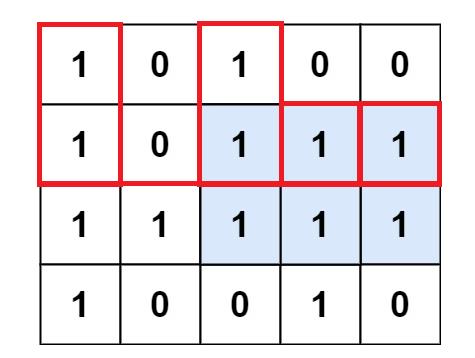
其它各层同理…如此，本题又被抽象成了LeetCode 84. 柱状图中最大的矩形。

int maximalRectangle(vector<vector<char>>& matrix) 

    int m = matrix.size();
    int n = matrix[0].size();
    // count[i][j]表示(i,j)及其上垂直方向有多少个连续1
    vector<vector<int>> count(m, vector<int>(n));
    for (int i = 0; i < m; ++i)
    
        for (int j = 0; j < n; ++j)
        
            if (i == 0)
                count[i][j] = matrix[i][j] == '1';
            else
                count[i][j] = matrix[i][j] == '1' ? 1 + count[i - 1][j] : 0;
        
    

    // 遍历第i行，count[i][j]表示当前行第j列的矩形高度
    // 我们要求的就是它们形成的矩形的最大面积
    int res = 0;
    for (int i = 0; i < m; ++i)
    
        stack<int> st;
        vector<int> lmin(n); // 左边比count[i][j]小的矩形所在列
        vector<int> rmin(n); // 右边比count[i][j]小的矩形所在列

        for (int j = 0; j < n; ++j)
        
            while (!st.empty() && count[i][st.top()] >= count[i][j])
            
                st.pop();
            
            lmin[j] = st.empty() ? -1 : st.top();
            st.push(j);
        

        st = stack<int>();
        for (int j = n - 1; j >= 0; --j)
        
            while (!st.empty() && count[i][st.top()] >= count[i][j])
            
                st.pop();
            
            rmin[j] = st.empty() ? n : st.top();
            st.push(j);
        

        // [lmin[j] + 1, rmin[j] - 1]的值都大于等于count[i][j]
        // 即count[i][j]在该范围内能够作为矩形的高
        for (int j = 0; j < n; ++j)
        
            res = max(res, (rmin[j] - lmin[j] - 1) * count[i][j]);
        
    

    return res;