统计学习方法笔记-概述

Posted 2022-11-26 xiaoranone

统计学习方法笔记

缘起

统计学习方法是李航博士的经典只作，也是很多学习机器学习的同学入门必备的书籍。这本书结合理论和习题，可深可浅的讲述了机器学习算法的原理。之前也读过一遍这本书，现在之所以写《统计学习方法》笔记，主要是和两个小伙伴有一个学习计划，我们每两周进行一个分享会，然后我们的第一本书选择的就是李航博士的《统计学习方法》。这里主要是整理分享会中的内容，希望对大家有所帮助。

统计学习方法概论

统计学习有自己的定义，主要是基于数据构建概率统计模型并运用该模型对未知数据进行预测和分析的一门学科。这里我们不管统计学习的方法的定义，就把它理解为机器学习，从数据出发，通过降低相应的损失函数来得到一个在未来数据集合上表现良好的模型。之后我们就用机器学习替换统计学习，这里我们简单的认为他们是一样的东西。

机器学习三种方式

定义：
训练数据 T=($x_1,y_1$),($x_2,y_2$),…,($x_N,y_N$); $x_i$对应的是一个n维的向量，$y_i$是其对应的标记数据，我们的目标是对应给定未知的$x_j$来预测其对应的$y_j$值。

1. 监督学习： 在训练数据中，所有的$x_i$都对应有相应的$y_i$ 。
2. 半监督学习： 在训练数据中，只有一部分数据的$x_i$都对应有相应的$y_i$，其他一部分数据只有x，没有y。
3. 无监督学习： 在训练数据中，所有的$x_i$都没有相应的$y_i$ 。

统计学习(机器学习)三要素

统计方法 = 模型（model）+ 策略（strategy）+ 算法（algorithm）

机器学习 = 数据（data） + 模型（model） + 优化方法（optimal strategy）

监督学习问题形式化：主要有两个阶段（学习模型：基于数据、算法、优化）和预测未知数据。

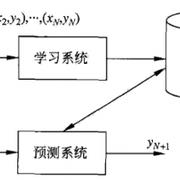
监督学习问题

模型（model）

基于数据，我们需要考虑的问题是需要学习什么样的模型，首先监督学习，半监督学习或者无监督学习，我们主要是如何从决策函数的集合中学习到最有的函数，这里的函数是广义的代表，不是所谓简单的f(x)。假设函数空间function_set,:
$$fs=f|Y=f(X)$$

X是向量，f(X)：是一个函数的代表，有时候也可以是概率函数。

策略（strategy）

策略就是我们在机器学习模型中，常提到的损失函数。这是来表示模型的好坏的指标，一般情况下，我们使用这个函数的值来表示得到的模型的好坏。一般记作：$L(Y,f(x))$.
常用的所示函数如：

1. 0-1损失函数（0-1 loss function）
   $$L(Y,f(X))=\begin{array}{ll}1,& Y̸=f(x)\\ 0,& y=f(x)\end{array}$$
   2.平方损失函数（qurdratic loss function）
   $$L(Y,f(x))=(Y-f(X){)}^2$$

3.绝对损失函数（absolute loss function）
$$L(Y,f(x))=|(Y-f(X))|$$

4.对数损失函数（logarithmic loss function; P(Y|X)表示X的情况下得到Y的概率。
$$L(Y,P(Y|X))=-logP(Y|X)$$

一般情况下，在给定数据的情况下，我们一般最小化所有训练数据的误差叫做经验风险最小化。之后只需要求解让经验风险最小化的参数即可。经验风险最小化：
$$mi{n}_{f\in F}=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))$$
当数据量很大的情况下，使用经验风险最小化，可以得到不错的模型，但是当数据量很少的情况下，就会产生过拟合。我们可以在经验风险最小化的基础上加上正则项来防止过拟合，这叫做结构风险最小化。
$$mi{n}_{f\in F}(f)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$$
$\lambda$是中和参数，来平衡模型复杂度和经验风险之间的关系。

算法

主要表示的是计算方法，例如梯度下降，Adam算法，牛顿迭代方法等。

模型的评估和模型的选择

一般情况下，我们在训练模型的时候，会将数据划分为：所有数据=训练数据集合+验证数据集合+测试数据集合。我们根据训练数据集合得到模型，这时候会产生一个训练误差，我们会根据验证数据的误差来调优一个模型的参数，会得到一个验证误差。之后会将的得到的最有的模型应用到测试数据集上，得到测试误差。判断这个模型的预测能力和泛化能力。

1. 数据如何划分？
   我们一般选择交叉验证的方式来划分数据集合

• 简单交叉验证: 随机将数据分成两部分，一般是8-2或者7-3，分别作为训练和验证集合。
• S折交叉验证: 将数据划分成S分，依次用其中的S-1个子集作为训练数据，剩下的作为验证集合，最后平均。
• 留一交叉验证: S=N，一般不使用这种方式。

2. 怎么比较三种误差？
   我们的目的是得到模型在测试集合和未来的数据集合上变现良好，这表示我们的模型泛化能力要强，一般情况下我们会使用经验风险加正则项的结构经验误差来进行优化，常用的正则项有$(L_0,L_1,L_2)$范式。如果训练误差过小，测试误差却大，表示产生了过拟合，具体的可以看下面这个图。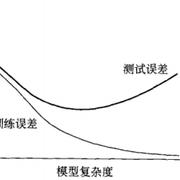

训练误差和测试误差与模型复杂度的关系

生成模型和判别模型

1. 判别模型，直接理解可以直接得出最后的结果，可以直接又数据学习到预测函数f(X)或者条件概率分别P(Y|X)的模型。代表: k近邻、感知机、决策树、逻辑斯蒂回归、最大熵模型、支持向量机、提升方法和条件随机场等。
2. 生成模型，需要先学习到联合概率分布P(X,Y)，之后在求出条件概率分布P(Y|X)的模型。代表：朴素贝叶斯和因马尔科夫模型。

一般需要解决的问题

首先我们需要明确一点，不管是什么问题，他们的输入都一样，不一样的是使用损失函数和输出值。

1. 分类问题: 输入X，损失函数交叉熵，0-1损失，输出是有限的离散值
2. 回归问题: 输入X，损失函数平方差，输出是无限的连续实数值
3. 标注问题: 输入X，损失函数交叉熵等，输出是的一个序列

感谢:

感谢小伙伴王**的分享。
生活如此，问题不打。喵～